朴素贝叶斯
http://zh.wikipedia.org/wiki/%E6%9C%B4%E7%B4%A0%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%88%86%E7%B1%BB%E5%99%A8
朴素贝叶斯概率模型
理论上,概率模型分类器是一个条件概率模型。
独立的类别变量 有若干类别,条件依赖于若干特征变量
有若干类别,条件依赖于若干特征变量 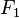 ,
,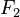 ,...,
,...,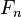 。但问题在于如果特征数量
。但问题在于如果特征数量 较大或者每个特征能取大量值时,基于概率模型列出概率表变得不现实。所以我们修改这个模型使之变得可行。 贝叶斯定理有以下式子:
较大或者每个特征能取大量值时,基于概率模型列出概率表变得不现实。所以我们修改这个模型使之变得可行。 贝叶斯定理有以下式子:
用朴素的语言可以表达为:
实际中,我们只关心分式中的分子部分,因为分母不依赖于 而且特征
而且特征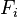 的值是给定的,于是分母可以认为是一个常数。这样分子就等价于联合分布模型。
的值是给定的,于是分母可以认为是一个常数。这样分子就等价于联合分布模型。
现在“朴素”的条件独立假设开始发挥作用:假设每个特征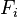 对于其他特征
对于其他特征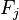 ,
,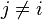 是条件独立的。这就意味着
是条件独立的。这就意味着
对于 ,所以联合分布模型可以表达为
,所以联合分布模型可以表达为
这意味着上述假设下,类变量 的条件分布可以表达为:
的条件分布可以表达为:
其中 (证据因子)是一个只依赖与
(证据因子)是一个只依赖与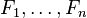 等的缩放因子,当特征变量的值已知时是一个常数。 由于分解成所谓的类先验概率
等的缩放因子,当特征变量的值已知时是一个常数。 由于分解成所谓的类先验概率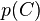 和独立概率分布
和独立概率分布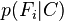 ,上述概率模型的可掌控性得到很大的提高。如果这是一个
,上述概率模型的可掌控性得到很大的提高。如果这是一个 分类问题,且每个
分类问题,且每个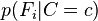 可以表达为
可以表达为 个参数,于是相应的朴素贝叶斯模型有(k − 1) + n r k个参数。实际应用中,通常取
个参数,于是相应的朴素贝叶斯模型有(k − 1) + n r k个参数。实际应用中,通常取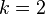 (二分类问题),
(二分类问题), (伯努利分布作为特征),因此模型的参数个数为
(伯努利分布作为特征),因此模型的参数个数为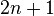 ,其中
,其中 是二值分类特征的个数。
是二值分类特征的个数。
[编辑]
性别分类
问题描述:通过一些测量的特征,包括身高、体重、脚的尺寸,判定一个人是男性还是女性。
[编辑]训练
训练数据如下:
| 性别 | 身高(英尺) | 体重(磅) | 脚的尺寸(英尺) |
|---|---|---|---|
| 男 | 6 | 180 | 12 |
| 男 | 5.92 (5'11") | 190 | 11 |
| 男 | 5.58 (5'7") | 170 | 12 |
| 男 | 5.92 (5'11") | 165 | 10 |
| 女 | 5 | 100 | 6 |
| 女 | 5.5 (5'6") | 150 | 8 |
| 女 | 5.42 (5'5") | 130 | 7 |
| 女 | 5.75 (5'9") | 150 | 9 |
假设训练集样本的特征满足高斯分布,得到下表:
| 性别 | 均值(身高) | 方差(身高) | 均值(体重) | 方差(体重) | 均值(脚的尺寸) | 方差(脚的
尺寸) |
|---|---|---|---|---|---|---|
| 男性 | 5.855 | 3.5033e-02 | 176.25 | 1.2292e+02 | 11.25 | 9.1667e-01 |
| 女性 | 5.4175 | 9.7225e-02 | 132.5 | 5.5833e+02 | 7.5 | 1.6667e+00 |
我们认为两种类别是等概率的,也就是P(male)= P(female) = 0.5。在没有做辨识的情况下就做这样的假设并不是一个好的点子。但我们通过数据集中两类样本出现的频率来确定P(C),我们得到的结果也是一样的。
[编辑]测试
以下给出一个待分类是男性还是女性的样本。
| 性别 | 身高(英尺) | 体重(磅) | 脚的尺寸(英尺) |
|---|---|---|---|
| sample | 6 | 130 | 8 |
我们希望得到的是男性还是女性哪类的后验概率大。男性的后验概率通过下面式子来求取
女性的后验概率通过下面式子来求取
证据因子(通常是常数)用来是各类的后验概率之和为1.
证据因子是一个常数(在正态分布中通常是正数),所以可以忽略。接下来我们来判定这样样本的性别。
 ,其中
,其中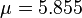 ,
,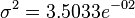 是训练集样本的正态分布参数. 注意,这里的值大于1也是允许的 – 这里是概率密度而不是概率,因为身高是一个连续的变量.
是训练集样本的正态分布参数. 注意,这里的值大于1也是允许的 – 这里是概率密度而不是概率,因为身高是一个连续的变量.
由于女性后验概率的分子比较大,所以我们预计这个样本是女性。
posted on 2013-08-10 10:40 berkeleysong 阅读(324) 评论(0) 收藏 举报

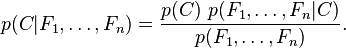

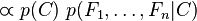
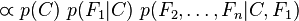
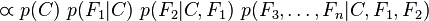


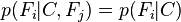
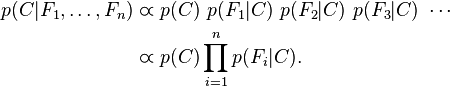
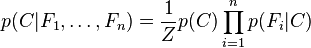
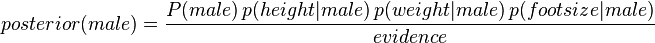
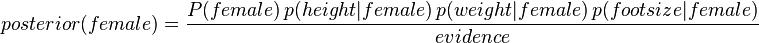



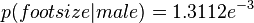
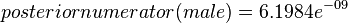


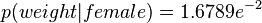




 浙公网安备 33010602011771号
浙公网安备 33010602011771号