斜率优化
什么是斜率优化？
通常我们在做动态规划的时候，会遇到如下形式的方程
$\Large f(i)=min(f(j)+w(j,i))$
对于i来说，什么时候取j比取t要好呢？
显然是当$f(j)+w(j,i)\le f(t)+w(t,i)$时
如果我们可以将式子化简成$\large\frac{A(j)-A(t)}{B(j)-B(t)}\le C(i)$(一侧与i无关，一侧只与i有关)的形式，且C是单调的
设$value(t,j)=\large\frac{A(j)-A(t)}{B(j)-B(t)}$
我们就可以维护一个关于value的单调队列从而快速求出i的决策
具体做法
每次向队列中加入一个元素时，算一下它和队尾元素的value
如果这个值$\le$队尾和队中倒数第二个元素的value就弹出队尾元素
(当队尾元素比队中倒数第二个元素优时，要加入的元素就已经比队尾元素优了)
如果队首两个元素的value$\le$当前的C(i)时，弹出第一个元素
名字来源
如果我们把(A(j),B(j))当成二维平面上的一个点
那么value就是两个点直线的斜率
单调队列中相邻两个点的斜率是单调递增的，如下图
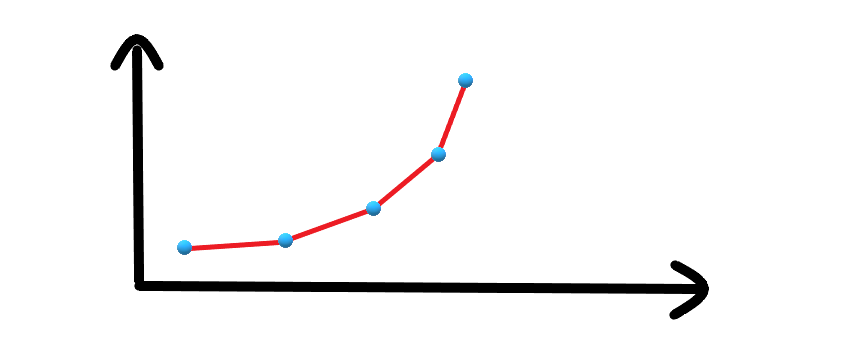
其实就是维护了一个下凸壳，所以说是斜率优化
