欧拉定理 费马小定理

欧拉定理

定义：若n,a为正整数，且n,a互质，则$a^{\varphi(n)}\equiv 1\ (mod\ n)$

证明：

设小于n与n互质的数分别为$x_1,x_2,x_3……x_{\varphi(n)}$

设$m_1=a*x_1,m_2=a*x_2,m_3=a*x_3,……,m_{\varphi(n)}=a*x_{\varphi(n)}$

可推出

1.所有mi中没有同余的。

证明：

假设mi和mj同余,则$m_i-m_j\equiv 0\ (mod\ n)$设$m_q=m_i-m_j\in \{m_1,m_2,……,m_{\varphi(n)}\}$

这与$n,a$互质和$n,x_q$互质冲突，所以mi中没有同余的

 2.所有mi%n与n互质。

证明：

假设mi%n=r，且gcd（r，n）!=1，则gcd（a*xi,n）=gcd（r，n）!=1

这与n和a，xi互质冲突，故所有mi%n与n互质。

由前两条结论可以推出

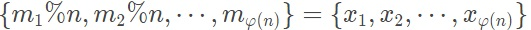
所以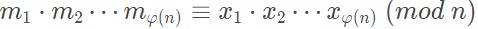

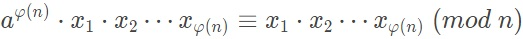
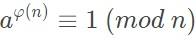
证明完毕

费马小定理

定义：a是不能被质数p整除的正整数，则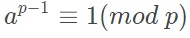

证明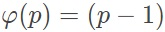：,由欧拉定理得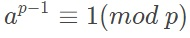

推论：对于任意正整数a，有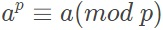

证明：对于a能整除p情况显然成立，对于a不能被p整除的情况，相当于费马小定理