统计学习方法第二版第五章决策树笔记

1. 决策树模型与学习

1.1 决策树模型

1.1.1 定义

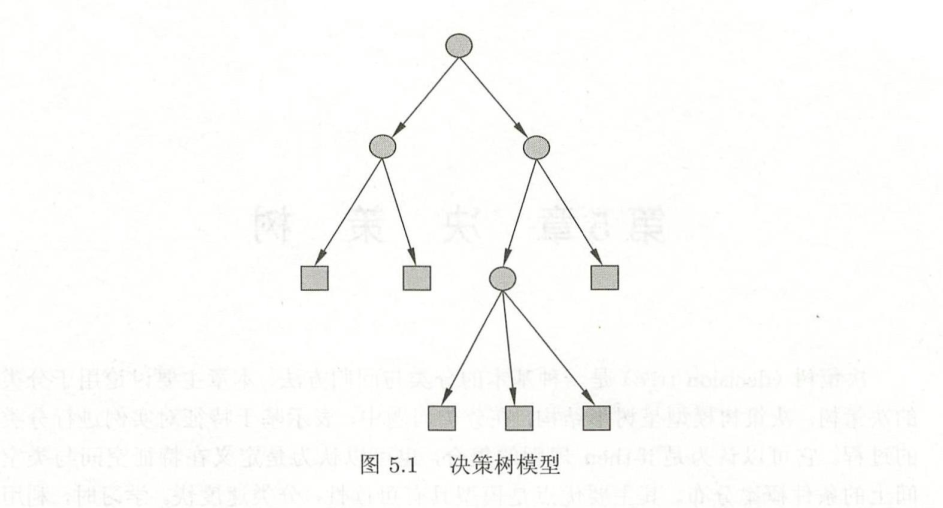
• 用决策树分类，从根结点开始，对一实例的某一特征进行测试，根据测试结果，将实例分配到其子结点这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中

1.1.2 目的和流程

1.1.2.1 目的：

1）产生一棵泛化能力强，处理未见示例能力强的决策树

1.1.2.2 流程：

1.2 决策树与if-then规则

1.2.1 过程

• 可以将决策树看成一个if-then规则的集合。由决策树的根结点到叶结点间每一条路径构建一条规则;路径上内部结点的特征对应着规则的条件，而叶节点的类对应着规则的结论

1.2.2 性质

• 互斥并且完备（这就是说，每一个实例都被一条路径或一条规则所覆盖，而且只被条路径或一条规则所覆盖。）

1.3 决策树与条件概率分布

• 决策树还表示给定特征条件下类的条件概率分布。
• 这一条件概率分布定义在特征空间的一个划分上。将特征空间划分为互不相交的单元(cell)或区域(region)，并在每个单元定义一个类的概率分布就构成一个条件概率分布。
• 决策树的一条路径对应于划分中的一个单元。决策树所表示的条件概率分布由各个单元给定条件下类的条件概率分布组成。
• 假设X表示特征的随机变量，Y为表示类的随机变量，那么这个条件概率分布可以表示为P(Y|X)。X的取值于给定划分下单元的集合，Y取值于类的集合。
• 各叶结点（单元）上的条件概率往往偏向某一个类，既属于某一类的概率较大。
• 决策树分类时将该结点的实例强行分到条件概率大的那一类去。

1.4 决策树学习

• 决策树学习是由训练数据集估计条件概率模型
• 决策树学习用损失函数实现条件概率模型不仅对训练数据有很好的拟合而且对未知数据有很好的预测
• 决策树学习的损失函数通常是正则化的极大似然函数，学习策略是以损失函数为目标函数的最小化
• 算法包含特征选择、决策树的生成与决策树的剪枝工程
• 决策树的生成只考虑局部最优，决策树的剪枝考虑全局最优

2. 特征选择

2.1 特征选择问题

2.1.1 定义

• 特征选择在于选取对训练数据具有分类能力的特征，决定用哪个特征来划分特征空间这样可以提高决策树学习的效率。

2.1.2 准则

• 信息增益或信息增益比

2.2 信息增益

2.2.1 熵

2.2.2 条件熵

2.2.3 信息增益

2.2.3.1 定义：

1）表示得知特征X的信息而使得类Y的信息的不确定性减少程度

2.2.3.2 算法：

2.3 信息增益比

• 以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比(information gain ratio) 以对这一问题进行校正。这是特征选择的另一准则。
  

3. 决策树的生成

3.1 ID3算法

3.1.1 定义

3.1.2 说明

• 分类算法
• ID3相当于用极大似然法进行概率模型选择
• ID3只有树的生成，所以该算法容易过拟合

3.2 C4.5的生成算法

3.2.1 定义

3.2.2 说明

• 分类算法
• 使用信息增益比

4. 决策树的剪枝

4.1 定义

4.2 剪枝实现

4.3 算法

4.4 预剪枝

• 在构造决策树的同时进行剪枝。
• 所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值。
• 例如：熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支

4.5 后剪枝

• 决策树构造完成后进行剪枝。
• 剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。
• 如果满足阈值要求，则这一组节点可以合并一个节点，其中包含了所有可能的结果。15

5. CART算法

5.1 简介

5.1.1 定义

5.1.2 算法步骤

5.2 CART生成

5.2.1 回归树生成

5.2.1.1 回归树模型：

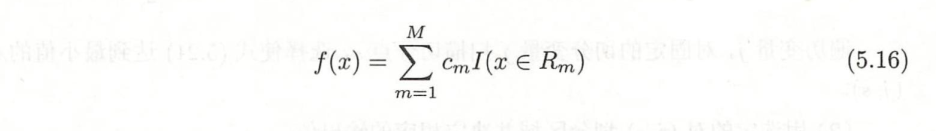
5.2.1.2 算法：

5.2.2 分类树生成

5.2.2.1 基尼系数：

5.2.2.2 A特征下集合D的基尼系数：

5.2.2.3 算法：

5.2.2.4 停止条件：

5.3 CART剪枝

5.3.1 算法