统计学习方法第二版第四章朴素贝叶斯法笔记

1. 朴素贝叶斯法的学习与分类

1.1 基本方法

1.1.1 先验概率分布

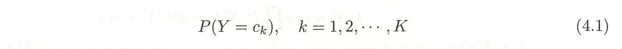
1.1.2 条件概率分布

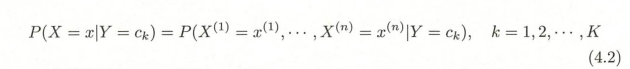
1.1.3 条件独立性假设

1.1.3.1 条件概率分布的参数个数：

1.1.3.2 条件独立性假设：

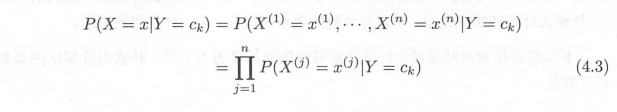
1.1.4 后验概率分布

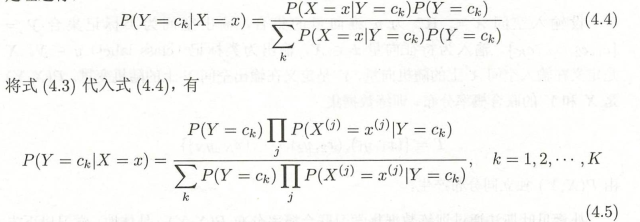
1.1.5 朴素贝叶斯分类器

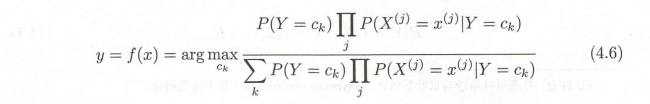
1.2 后验概率最大化的含义

极小化说明：

\[\begin{aligned} f\left ( x \right ) &=arg\underset{y\epsilon Y}min\sum_{k=1}^{K}L\left ( c_{k},y \right )P\left ( c_{k}|X=x \right )\\ \Rightarrow& =arg\underset{y\epsilon Y}min\sum_{k=1}^{K}L\left ( c_{k},y \right )\cdot \left [ P\left (y=c_{k}|X=x \right )+ P\left (y\neq c_{k}|X=x \right )\right ]\\ &因为是0-1损失函数则P\left (y=c_{k}|X=x \right )时L=0，P\left (y\neq c_{k}|X=x \right )时L=1\\ \Rightarrow& =arg\underset{y\epsilon Y}min\sum_{k=1}^{K}P\left (y\neq c_{k}|X=x \right )\\ \Rightarrow& =arg\underset{y\epsilon Y}min\left [1- P\left (y=c_{k}|X=x \right )\right ]\\ \Rightarrow& =arg\underset{y\epsilon Y}maxP\left (y=c_{k}|X=x \right )\\ \end{aligned} \]

2. 朴素贝叶斯法的参数估计

2.1 极大似然估计

2.2 学习与分类算法

2.2.1 朴素贝叶斯算法

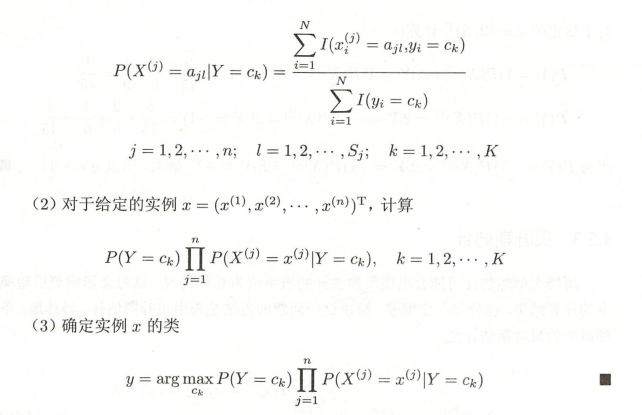
2.2.2 具体流程

2.2.2.1 对于第（2）步计算的处理：

1）找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2）统计得到在各类别下各个特征属性的条件概率估计。即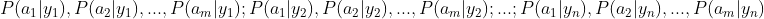
3）如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

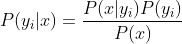
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

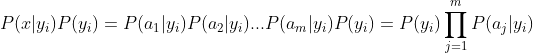
2.2.2.2 流程：

1）准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
2）分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。
3）应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

2.3 贝叶斯估计

2.4 分类器评价

分类器的正确率指分类器正确分类的项目占所有被分类项目的比率。通常使用回归测试来评估分类器的准确率，最简单的方法是用构造完成的分类器对训练数据进行分类，然后根据结果给出正确率评估。但这不是一个好方法，因为使用训练数据作为检测数据有可能因为过分拟合而导致结果过于乐观，所以一种更好的方法是在构造初期将训练数据一分为二，用一部分构造分类器，然后用另一部分检测分类器的准确率