统计学习方法第二版第三章K近邻算法笔记

1.K近邻算法

1.1 定义

说明：分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测，因此KNN算法不能得到一个函数或者概率分布来表示学习过程

1.2 一般过程

1）计算已训练集中样本与待测样本之间的距离；
2）按距离排序；
3）选取与当前样本距离最小的k个邻居样本；
4）确定此k个样本中各个类别的频率；
5）频率最高的类别作为该样本的预测分类。

2. K近邻模型

2.1 模型

2.2 距离的度量

2.2.1 \(L_{p}\)距离

2.2.1.1 定义：

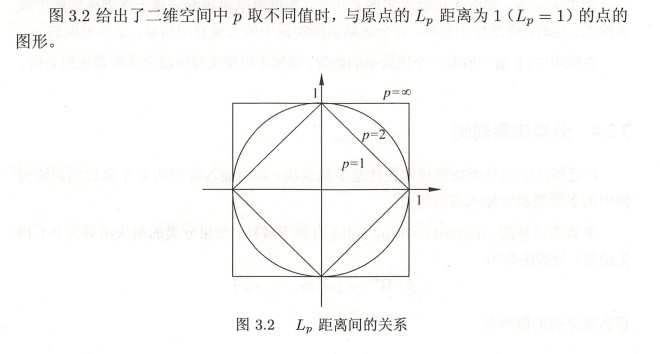
2.2.1.2 欧氏距离：

2.2.1.3 曼哈顿距离：

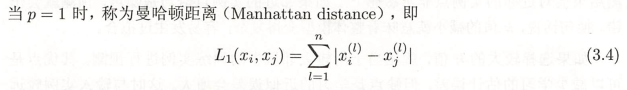
2.2.1.4 \(P\rightarrow \infty\)切比雪夫距离：

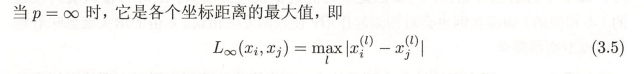
说明：计算距离需要对数值型数据做归一化

2.3 K值的选择

K值减小整体模型变得复杂，容易引起过拟合；K值增大整体模型变得简单，容易引起欠拟合；在应用中，K值一般取一个较小的值，采用交叉验证法、贝叶斯准则或bootstrap来选取最优的K值，K一般低于训练样本数的平方根

2.4 分类决策规则

3. K近邻法的实现：kd树

3.1 构造kd树

3.1.1 定义

注意：平衡kd树的搜索时效率未必最优

3.2 搜索kd树

3.2.1 定义

3.2.2 搜索kd树的时间复杂度