RSA规范 2.2版精要总结基于《RFC 8017：PKCS #1：RSA 加密规范版本 2.2》

本文总结开发者用到的RSA规范知识。规范原文 (RFC 8017：PKCS #1：RSA 加密规范版本 2.2 --- RFC 8017: PKCS #1: RSA Cryptography Specifications Version 2.2 (rfc-editor.org))

摘要

本文档提供了实施基于 RSA 算法的公钥密码学，
涵盖

加密原语、
加密方案、
带附录的签名方案
和 ASN.1 语法，用于表示key 以及标识schemes。

1. 引言

本规范涵盖以下几个方面

加密原语 Cryptographic primitives
加密方案 Encryption schemes
ASN.1 语法，用于表示键和标识方案 ASN.1 syntax for representing keys and for identifying the schemes

第 3 节定义了 RSA 公钥和私钥类型。

第 4 节和第 5 节定义了几个基元或基本数学运算。数据转换原语位于第 4 节中，密码学原语（encryption-decryption 和 signature-verification）位于第 5 节中。

第 6、7 和 8 节介绍本文档中的加密和签名方案。第 6 节给出了概述。除了 PKCS #1 v1.5 中的方法外，第 7 节还定义了基于最佳非对称加密填充（[OAEP）全称 Optimal Asymmetric Encryption Padding 的加密方案，第 8 节定义了基于概率签名方案（PSS）全称Probabilistic Signature Scheme 的签名方案和附录。

第 9 节定义了第 8 节中签名方案的编码方法。

附录 A 定义了第 3 节中定义的 Key 以及第 7 节和第 8 节中的方案schemes 的 ASN.1 语法。

附录 B 定义了本文档中使用的哈希函数和掩码生成函数（MGF），包括技术的 ASN.1 语法。

附录 C 给出了 ASN.1 模块。

附录 D 和 E 概述了 PKCS #1 的修订历史，并提供了有关公钥加密标准的一般信息。

3. 密钥类型

该规范支持所谓的“多素数”RSA，其中模数可能有两个以上的素因数。多质 RSA 的好处是，如果使用 CRT，解密和签名基元的计算成本较低。在单处理器平台上可以实现更好的性能，但在多处理器平台上可以实现更大的性能，其中涉及的模幂运算可以并行完成。

3.1. RSA 公钥

RSA 公钥由两个部分组成：

    n        the RSA modulus, a positive integer， 模
    e        the RSA public exponent, a positive integer，公开指数

3.2. RSA 私钥

以下两种表示形式之一：

（n， d）组成

    n       the RSA modulus, a positive integer，模
    d       the RSA private exponent, a positive integer，秘密指数

五元组（p， q， dP， dQ， qInv）和一个（可能为空的）三元组序列（r_i， d_i， t_i）组成

            p      the first factor, a positive integer
            q      the second factor, a positive integer
            dP     the first factor's CRT exponent, a positive integer
            dQ     the second factor's CRT exponent, a positive integer
            qInv   the (first) CRT coefficient, a positive integer
            r_i    the i-th factor, a positive integer
            d_i    the i-th factor's CRT exponent, a positive integer
            t_i    the i-th factor's CRT coefficient, a positive integer

4. 数据转换原语

为了与整数之间的转换，第一个八位字节被认为是以下转换基元中最高的the most significant。

4.1. I2OSP

I2OSP - 整数到八位字节字符串原语 Integer-to-Octet-String primitive
- 比如一个整数x，长度为Len，它的数值为

\[x = x_{Len-1} 256^{x_{Len-1}} + x_{x_{Len-2}} 256^{x_{Len-2}} + ... + x_{1} 256^1 + x_{0} \]

其中 $ 0 <=x_{[i]} < 256$ 。则结果就是 $X = x_{Len-1} x_{Len-2} x_{Len-3}... x_{1} x_{0}$

比如 Len = 128, 则

\[x = x_{127} 256^{127} + x_{126} 256^{126} + ... + x_{1} 256^1 + x_{0} \]

其中 $ 0 <=x_{[i]} < 256$ 。则结果就是 $X = x_{Len-1} x_{Len-2} x_{Len-3}... x_{1} x_{0}$

4.2. OS2IP

OS2IP - 八位字节字符串到整数原语 Octet-String-to-Integer primitive
- $x = x_{Len-1} 256^{Len-1} + x_{Len-2} 256^{Len-2} + ... + x_1 256 + x_0$

5. 密码学原语

本文档指定了四种类型的基元，

加密和解密
签名和验证

5.1. 加密和解密原语

5.1.1. RSAEP

（私钥采用第一种私钥形式 n,d）。另一种形式参加规范原文

全称RSA Encryption Primitive ，参数如下：

输入参数

  - m 消息代表 （message representative）
  - e 公共指数
  - n 模

输出参数

  - c 密文代表 （ciphertext representative）

过程即为：
 c = m^e mod n

5.1.2. RSADP

全称 RSA Decryption Primitive (RSADP) ，参数如下：

输入参数

  - c 密文代表 （ciphertext representative）
  - d 秘密指数
  - n 模

(输出)参数

  -  m 消息 代表 （meaasge representative）

过程即为：（私钥 采用第一种私钥形式 n,d）
 m = c^d mod n

5.2. 签名和验证原语

5.2.1. RSASP1

（私钥采用第一种私钥形式 n,d）。另一种形式参加规范原文
全称RSA Signature Primitive, version 1 (RSASP1) ，参数如下：

输入参数

  - d 秘密指数
  - n 模
  - m 消息代表 （message representative）

(输出)参数

  - s 签名值代表 （signature representative）

 s = m^d mod n

5.2.2. RSAVP1

全称 RSA Verification Primitive, version 1 ，参数如下：

输入参数

  - e 公开指数
  - n 模
  - s 签名值代表 （signature representative）

(输出)参数

  - m 消息代表 （message representative）

 m = s^e mod n

7. 加密方案

7.1. RSAES-OAEP

7.1.1. 加密操作

全称 RSAES-OAEP-ENCRYPT ((n, e), M, L)，参数如下：

选项

  - 哈希函数（hLen 表示哈希函数输出的八位字节长度）
  - MGF 掩码生成函数

输入参数

  - e 公开指数
  - n 模
  - M 消息，长度限制为 `mLen <= k - 2hLen - 2`
  - L 可选的 label 数据，如果未提供 L，则 L 的默认值为空字符串

(输出)参数

  - C 密文

过程:

参数检查 (消息长度不得超过mLen <= k - 2hLen - 2，label长度不得超过哈希函数的输入限制，比如 SHA-1 为 $2^{61} - 1$ 个八位字节 )
编码 EME-OAEP, 计算出编码值 EM

)

至于MGF的计算过程，见本笔记的 MGF计算规则

DB = lHash || PS || 0x01 || M
maskedDB = MGF(seed, hLen ) 异或 DB
maskedSeed = MGF(maskedDB,k-hLen-1) 异或 seed

如果 L 为空字符串，则对应的 Hash 值 lHash 对于不同的 Hash 选择，具有以下十六进制表示：

      SHA-1:   (0x)da39a3ee 5e6b4b0d 3255bfef 95601890 afd80709
      SHA-256: (0x)e3b0c442 98fc1c14 9afbf4c8 996fb924 27ae41e4 649b934c
                   a495991b 7852b855
      SHA-384: (0x)38b060a7 51ac9638 4cd9327e b1b1e36a 21fdb711 14be0743
                   4c0cc7bf 63f6e1da 274edebf e76f65fb d51ad2f1 4898b95b
      SHA-512: (0x)cf83e135 7eefb8bd f1542850 d66d8007 d620e405 0b5715dc
                   83f4a921 d36ce9ce 47d0d13c 5d85f2b0 ff8318d2 877eec2f
                   63b931bd 47417a81 a538327a f927da3e

RSA加密

m = OS2IP (EM)
c = RSAEP ((n, e), m).
C = I2OSP (c, k).

4.输出密文C。

7.1.2. 解密操作

全称RSAES-OAEP-DECRYPT （K, C, L），参数如下：

选项

  - 哈希函数（hLen 表示哈希函数输出的八位字节长度）
  - MGF 掩码生成函数

输入参数

  - d 秘密指数
  - n 模
  - C 密文值，长度为 私钥长度k
  - L 可选的 label 数据，如果未提供 L，则 L 的默认值为空字符串

(输出)参数

  - M 明文消息

过程:
1. 参数检查 (密文长度必须是CLen == k; 必须 k ≥ 2hLen + 2; 以及label长度不得超过哈希函数的输入限制，比如 SHA-1 为 $2^{61} - 1$ 个八位字节， )
2. RSA解密，得到 EM值
```
  c = OS2IP (C)
  m = RSADP (K, c)
  EM = I2OSP (m, k)
```

3.解析编码 EME-OAEP
3.1 把EM划分出三大块
0x00
maskedSeed
maskedDB
3.2 将 maskedSeed 再异或上 MGF(maskedDB,hLen) ，可以得到 Seed原数据
3.3 将 Seed做 MGF，得到 MGF(seed,k-hLen-1)
3.4 将 maskedDB 异或上 MGF(seed,k-hLen-1)，可得到 DB原数据。
3.5 将 DB拆解为 lHash || PS || 0x01 || M。 lHash往后查找到的第一个0x01作为边界，往后则取出M部分。就得到了消息值 M。

)
4. 输出明文消息 M。

至于MGF的计算过程，见本笔记的 MGF计算规则

7.2. RSAES-PKCS1-v1_5

7.2.1. 加密操作

RSAES-PKCS1-V1_5-ENCRYPT ((n, e), M) ，参数如下：

输入参数

     - (n, e)   公钥
     - M        消息，长度为mLen,此长度必须满足 mLen <= k - 11

输出参数

  -  C        密文数据

过程:
1. 参数检查 ( 明文消息长度必须满足mLen <= k - 11 )
2. EME-PKCS1-v1_5 编码，得到 EM值

RSA加密

m = OS2IP (EM).
c = RSAEP ((n, e), m)
C = I2OSP (c, k)

输出密文值 C。

7.2.2. 解密操作

RSAES-PKCS1-V1_5-DECRYPT (K, C)

Input: 输入：

K        RSA 私钥
C        密文，长度必须为 k。

K 是RSA 私钥； C 是要解密的密文，长度为 k 的八位字节字符串，其中 k 是 RSA 模数 n 的八位字节长度（以八位字节为单位）

Output: 输出：

      M        消息, 长度最大为 k - 11的八位字节字符串

过程：
1.参数检查，确保密文 C 的长度是 k ，且确保 k - 11≥ 0。
2.RSA解密，得到 EM值

   c = OS2IP (C)
  m = RSADP ((n, d), c)
  EM = I2OSP (m, k)

EME-PKCS1-v1_5 解码
3.1 解析
划分出 0x00 || 0x02 || 非零PS随机串 || 0x00 || M
M 就是消息的明文值。

3.2 输出消息M。

8. 签名方案（含附录）

含有附录，指的是：

需要将消息作为验证算法输入。而签名仅仅是消息的附录，不具备消息恢复功能。

8.1. RSASSA-PSS

8.1.1. 签名生成操作

Input: 输入：

      K        RSA私钥
      M        要被签名的消息

K 是签名者的 RSA 私钥； M是要签名的 M 条消息，一个八位字节字符串。

Output: 输出：

    S       签名值

S 是签名，长度为 k 的八位字节字符串，其中 k 是 RSA 模数 n 的八位字节长度（以八位字节为单位）

过程
1. EMSA-PSS 编码：将 EMSA-PSS 编码操作（第 9.1.1 节）应用于消息 M，以生成长度为 $ceil ((modBits - 1)/8)$ 八位字节的编码消息 EM，使得整数 OS2IP （EM）（请参阅第 4.2 节）的位长度最多为 modBits - 1，其中 modBits 是 RSA 模数 n 的长度（以位为单位）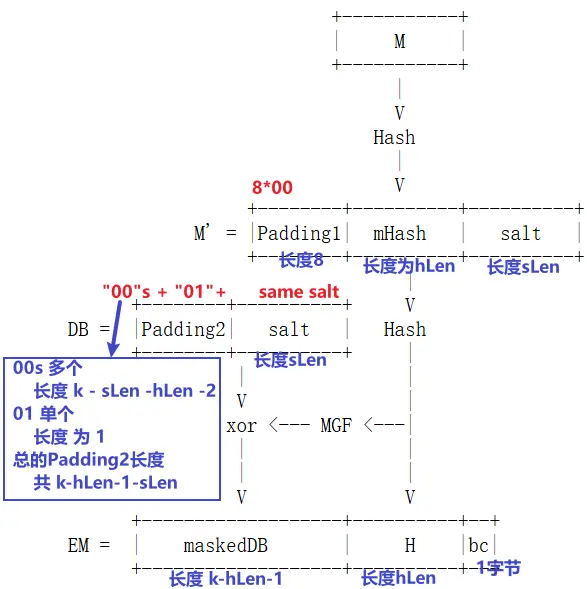

1.1. 典型盐长度为 hLen（哈希函数 Hash 的输出长度）和 0
1.2. 计算 mHash = Hash（M），长度为 hLen 的八位字节字符串
1.3. 生成一个长度为 sLen 的随机八位字节字符串 salt; 如果 sLen = 0，则 salt 为空字符串。
1.4. 生成 M' = （0x）00 00 00 00 00 00 00 00 00 00 00 ||mHash || salt ;
1.5. 生成一个八位字节字符串 Padding2，由 emLen - sLen - hLen - 2 个零八位字节组成。Padding2 的长度可以是 0。
1.6. 计算 DB = Padding2 ||0x01 || salt; 于是 DB 长度为 emLen - hLen - 1。
1.7. 计算 H = Hash（M'）
1.8. 计算 maskedDB = DB 异或 MGF(H, emLen - hLen - 1)。
1.9. 将 maskedDB 中最左侧八位字节的最左侧的 $8emLen - emBits$ 位设置为零
1.10. 得出 EM = maskedDB || H ||0xbc

RSA 签名

  m = OS2IP (EM)
  s = RSASP1 (K, m)
 S = I2OSP (s, k)

输出签名 S。

至于MGF的计算过程，见本笔记的 MGF计算规则

8.1.2. 签名验证操作

RSASSA-PSS-VERIFY （（n， e）， M， S），参数：
Input: 输入：

      (n, e)      签署者的RSA公钥
      M           消息
      S           签名值

(n,e) : 签名者的 RSA 公钥
M : 消息（就是它的签名需要验证）;是一个要验证的八位字节字符串
S : 签名，一个长度为 k 的八位字节字符串，其中 k 是 RSA 模数 n 的八位字节长度（以八位字节为单位）

输出参数：

“有效签名” 或 “无效签名”

步骤:

1. 长度检查: 签名 S 的长度必须是 k 个八位字节
1. RSA 验证：
  数据转换，然后通过RSAVP1原语，获得 EMSA-PSS编码值。

s = OS2IP (S)
m = RSAVP1 ((n, e), s)
EM = I2OSP (m, emLen)

1. EMSA-PSS 验证
  将 EMSA-PSS 验证操作（第 9.1.2 节）应用于消息 M 和编码的消息 EM，以确定它们是否一致
  Result = EMSA-PSS-VERIFY (M, EM, modBits - 1)
  Options:选项：

      Hash      哈希函数（hLen 表示哈希函数输出的八位字节长度）
      MGF      掩码生成函数
      sLen      以盐的八位字节为单位的预期长度

Input:输入：

      M           待验证的 M 消息
      EM        一个八位字节字符串 EM 编码的消息
      emBits   整数 OS2IP （EM） 的最大bit长度的八位字节字符串， 至少 8hLen + 8sLen + 9

Output输出:

"一致" or "不一致"

过程：
3.0 检查格式EMSA-PSS，比如最后一个字节必须是 0xbc，以及一些长度检查。
3.1. 计算 mHash。设 mHash = Hash（M），长度为 hLen 的八位字节字符串。
3.2. 从EM中 取出 maskedDB （最左边的 emLen - hLen - 1 长度），设 H 为下一系列 hLen 八位字节。
3.3 从maskedDB计算出原 DB，也就是异或上 MGF(H, emLen - hLen - 1)
3.4 拆解原DB，获的 salt值。
3.5 以 Padding1 || 计算M得到的mHash || 刚算出来的salt 作为M'
3.6 计算 Hash( M' )。看是否等于 H。等于则校验一致。不等于则校验不一致。

1. 输出验证结果

至于MGF的计算过程，见本笔记的 MGF计算规则

8.2. RSASSA-PKCS1-v1_5

8.2.1. 签名生成操作

Input: 输入：

      K        签名者的 RSA 私钥
      M        要签名的 M 条消息

Output: 输出：

      S        签名，长度为 k 的八位字节字符串

步骤：
1. EMSA-PKCS1-v1_5 编码：将 EMSA-PKCS1-v1_5 编码操作（第 9.2 节）应用于消息 M，以生成长度为 k 个八位字节的编码消息 EM：
过程

1.1 将哈希函数应用于消息 M，生成哈希值 H：

H = Hash(M)

1.2. 使用 DER 将哈希函数的算法 ID 和哈希值编码为 DigestInfo 类型的 ASN.1 值（请参阅附录 A.2.4），其中 DigestInfo 类型的语法为

DigestInfo ::= SEQUENCE {
                   digestAlgorithm AlgorithmIdentifier,
                   digest OCTET STRING
               }

第一个字段标识哈希函数，第二个字段包含哈希值。设 T 为 DigestInfo 值的 DER 编码（请参阅下面的注释），设 tLen 为 T 的八位字节长度。

1.3 生成一个八位字节字符串 PS，由 k - tLen - 3 个八位字节组成，十六进制值为 0xff。PS 的长度至少为 8 个八位字节。
1.4. 组装EM，输出 EM

对于附录 B.1 中提到的 9 个哈希函数，DigestInfo 值的 DER 编码 T 等于以下内容：
MD2: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 02 05 00 04 10 || H.
MD5: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 05 05 00 04 10 || H.
SHA-1: (0x)30 21 30 09 06 05 2b 0e 03 02 1a 05 00 04 14 || H.
SHA-224: (0x)30 2d 30 0d 06 09 60 86 48 01 65 03 04 02 04 05 00 04 1c || H.
SHA-256: (0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 01 05 00 04 20 || H.
SHA-384: (0x)30 41 30 0d 06 09 60 86 48 01 65 03 04 02 02 05 00 04 30 || H.
SHA-512: (0x)30 51 30 0d 06 09 60 86 48 01 65 03 04 02 03 05 00 04 40 || H.
SHA-512/224: (0x)30 2d 30 0d 06 09 60 86 48 01 65 03 04 02 05 05 00 04 1c || H.
SHA-512/256: (0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 06 05 00 04 20 || H.

RSA 签名：

m = OS2IP (EM)
s = RSASP1 (K, m)
S = I2OSP (s, k)

输出签名值

8.2.2. 签名验证操作

RSASSA-PKCS1-V1_5-VERIFY ((n, e), M, S)

Input: 输入：

      (n, e)  签署者的 RSA 公钥
      M       消息
      S        签名值

输出参数：

“有效签名” 或 “无效签名”

过程：

长度检查，确保S长度等于k。
RSA校验

2.1 数据转换，然后通过RSAVP1原语，获得 EMSA-PKCS1-V1_5编码值

s = OS2IP (S)
m = RSAVP1 ((n, e), s)
EM = I2OSP (m, k)

EMSA-PKCS1-v1_5 编码：将 EMSA-PKCS1-v1_5 编码操作（第 9.2 节）应用于消息 M，以生成长度为 k 个八位字节的第二个编码消息 EM'
比较编码消息 EM 和第二个编码消息 EM'。如果相同，则输出 “valid signature”;否则，输出 “Invalid Signature”

附录 A.ASN.1 语法

A.1. RSA 密钥表示法

本节定义 RSA 公钥和私钥的 ASN.1 对象标识符，并定义类型 RSAPublicKey 和 RSAPrivateKey。
这些定义的预期应用包括 X.509 证书、PKCS #8 [RFC5958] 和 PKCS #12 [RFC7292]

A.1.1. RSA 公钥语法

 RSAPublicKey ::= SEQUENCE {
             modulus           INTEGER,  -- n
             publicExponent    INTEGER   -- e
         }

A.1.2. RSA 私钥语法

RSAPrivateKey ::= SEQUENCE {
             version           Version,
             modulus           INTEGER,  -- n
             publicExponent    INTEGER,  -- e
             privateExponent   INTEGER,  -- d
             prime1            INTEGER,  -- p
             prime2            INTEGER,  -- q
             exponent1         INTEGER,  -- d mod (p-1)
             exponent2         INTEGER,  -- d mod (q-1)
             coefficient       INTEGER,  -- (inverse of q) mod p
             otherPrimeInfos   OtherPrimeInfos OPTIONAL
         }

MGF

MGF计算介绍

B.2. Mask Generation Functions 掩码生成函数

这里给出了一个掩码生成函数： MGF1 ，它基于哈希函数。
MGF1 与 IEEE1363] 和 ANSI X9.44 [ANSIX944] 中定义的掩码生成函数一致。
本文档的未来版本可能会定义其他掩码生成函数。

B.2.1. MGF1

MGF1 (mgfSeed, maskLen)

Options: 选项：

      Hash    哈希函数（hLen 表示哈希函数输出的长度（以八位字节为单位）

Input: 输入：

      mgfSeed  生成掩码的种子
      maskLen  以掩码的八位字节为单位的预期长度，最多 2^32 hLen

Output: 输出：

     mask，长度为 maskLen 的八位字节字符串

步骤：

设 T 为空的八位字节字符串。
对于从 0 到 $ceil(maskLen / hLen) - 1$的counter，请执行以下操作

ceil是向上取整。本质上上，是每次进行以下运算，拼接 hLen结果，拼接到后面，达到（至少有） maskLen 就收手。

C = I2OSP (counter, 4)                   整数转 4字节
T = T || Hash(mgfSeed || C)

输出 T 的前导 maskLen 八位字节作为octet string mask(八位字节字符串掩码)。也就是如果T此时多于maskLen，后面会被截断舍去。

结果生成的计算模式，大致长下面这样：

Hash(mgfSeed||0x00000000) || Hash(mgfSeed||0x00000001) || Hash(mgfSeed||0x00000002)
... Hash( mgfSeed || I2OSP(ceil(maskLen/hLen)-1,4) )

posted @ 2024-09-08 17:14 北壹阅读(1116) 评论(0) 收藏举报

刷新页面返回顶部

北壹的知识分享

RSA规范 2.2版精要总结 基于《RFC 8017：PKCS #1：RSA 加密规范版本 2.2》

摘要

1. 引言

3. 密钥类型

3.1. RSA 公钥

3.2. RSA 私钥

4. 数据转换原语

4.1. I2OSP

4.2. OS2IP

5. 密码学原语

5.1. 加密和解密原语

5.1.1. RSAEP

5.1.2. RSADP

5.2. 签名和验证原语

5.2.1. RSASP1

5.2.2. RSAVP1

7. 加密方案

7.1. RSAES-OAEP

7.1.1. 加密操作

7.1.2. 解密操作

7.2. RSAES-PKCS1-v1_5

7.2.1. 加密操作

7.2.2. 解密操作

8. 签名方案（含附录）

8.1. RSASSA-PSS

8.1.1. 签名生成操作

8.1.2. 签名验证操作

8.2. RSASSA-PKCS1-v1_5

8.2.1. 签名生成操作

8.2.2. 签名验证操作

附录 A.ASN.1 语法

A.1. RSA 密钥表示法

A.1.1. RSA 公钥语法

A.1.2. RSA 私钥语法

MGF

B.2. Mask Generation Functions 掩码生成函数

B.2.1. MGF1

RSA规范 2.2版精要总结基于《RFC 8017：PKCS #1：RSA 加密规范版本 2.2》