多元线性回归

多元线性回归

标签： 线性回归 多元线性回归 吴恩达

---

1. 假设函数

\[h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 ＋\cdots+\theta_nx_n \]

　　假设\(x_0 = 1\)，则有$$h_\theta(x) = \theta_0x_0 + \theta_1x_1 + \theta_2x_2 ＋\cdots+\theta_nx_n$$
　
　　即 $$h_\theta(x) = \theta^TX $$
　　其中:

　　$$X = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\quad
　　
　　\theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{bmatrix}\quad$$
　　

2. 代价函数

\[J(\theta) = \frac{1}{2m}\sum_{i=0}^{m}(\theta^Tx^{(i)}-y^{(i)})^2 \]

或者

\[J(\theta) = \frac{1}{2m}\sum_{i=0}^{m}((\sum_{j=0}^{n}\theta_jx^{(i)}_j)-y^{(i)})^2 \]

代价函数依据上一篇博客所讲述的内容以及假设函数推导而来。即：

\[J(\theta) = \frac{1}{2m}\sum_{i=0}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 \]

　　

3. 梯度下降

(1) 方法

　　Repeat {
　　　　\(\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)\)
　　}
　　同时 更新每个参数。
　　容易计算得：

　　$$\frac{\partial}{\partial\theta_j}J(\theta) = \frac{1}{m}\sum_{i=0}^{{m}(h_\theta(x})-y^{(i)})x_j$$

　　因此得到：

　　$$\theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=0}^{{m}(h_\theta(x})-y^{(i)})x_j$$
　　

(2) 特征缩放

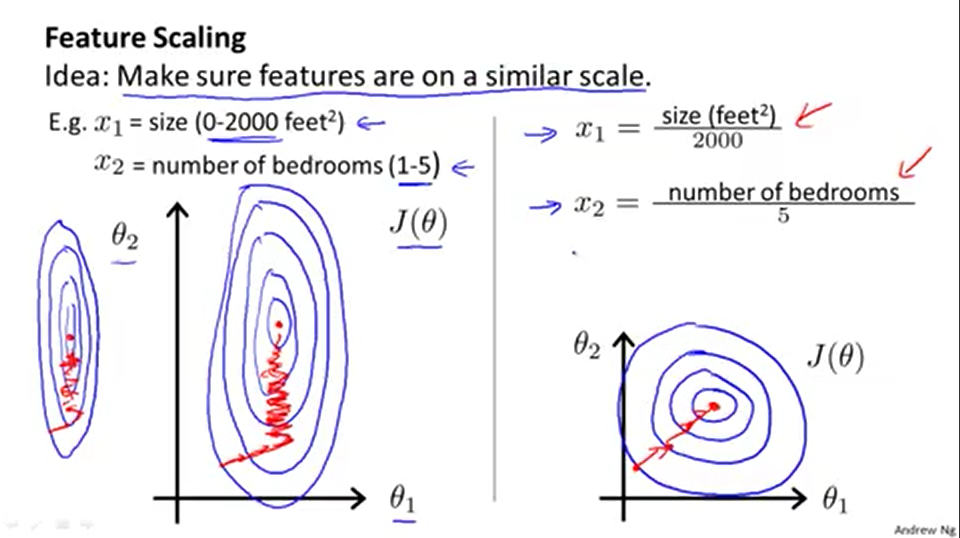
特征缩放的原因如上图所示，（图片来自吴恩达教授机器学习公开课视频截图），特征缩放能使得梯度下降更快地收敛。

(3) 学习速率 \(\alpha\)

\(\alpha\)的值如果太大，容易造成震荡或不收敛，太小则学习速率太慢。实际操作中根据经验或尝试逐步调节参数。