统计学习方法（第一章）

（一）统计学习方法三要素：模型、策略和算法

方法=模型+策略+算法

（1）     模型：监督学习中，模型就是所要学习的条件概率分布或决策函数，模型的假设空间包含所有可能的条件概率分布或决策函数。

（2）     策略：有了模型的假设空间，接着就是考虑按照什么样的准则学习或选择最优的模型，统计学习的目标就是从假设空间中选取最优模型。

a)       损失函数和风险函数：常用的损失函数有0-1损失函数；平方损失函数；绝对损失函数；对数损失函数或对数似然损失函数；损失函数值越小，模型越好。

b)      经验风险最小化(ERM)与结构风险最小化（SRM）

（3）     算法：是指学习模型的具体计算方法。统计学习基于训练数据集，根据学习策略，从假设空间中选择最优模型，最后需要考虑用什么样的方法求解最优模型。归结为最优化问题，统计学习的算法称为求解最优化问题的算法。

（二）模型评估与模型选择

（1）训练误差与测试误差

基于损失函数的模型的训练误差和模型的测试误差就是学习方法评估的标准。

（2）过拟合与模型选择

一味提高对训练数据的预测能力，所选模型的复杂度则往往会比真模型更高，这种现象称为过拟合（over-fitting），过拟合是指学习时选择的模型所包含的参数过多，以致于出现这一模型对已知数据预测的很好，但对未知数据预测的很差的现象。模型选择旨在避免过拟合并提高模型的预测能力。

（三）正则化与交叉验证

（1）正则化

模型选择的典型方法，是结构风险最小化策略的实现，是在经验风险上加一个正则化项或罚项。正则化一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。

形式：不固定，例如回归问题中，损失函数是平方损失，正则化项可以是参数向量的L2范数。

符合奥卡姆剃刀（Occam’s razor）原理，原理应用于模型选择时，即在所有的可能选择的模型中，能给很好的解释已知数据却简单，就是最好的模型，也是应该选择的模型。从贝叶斯估计的角度看，正则化对应于模型的先验概率，可假设复杂的模型有较大的先验概率，简单的模型有较小的先验概率。

（2）交叉验证

思想：重复的使用数据，把给的的数据进行切分，将切分的数据集组合为训练集与测试集，在此基础上反复进行训练、测试以及模型选择。

方法：

简单交叉验证-随机将已给数据分为两部分，一部分训练集，一部分作为测试集，然后用训练集在各种条件下（不同参数个数）训练模型，从而得到不同的模型；在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

S折交叉验证（S-fold cross validation）-首先随机地将已给数据切分为S个互不相交的大小相同的自己，然后利用S-1个子集数据训练模型，利用余下的子集测试模型。将这一过程对可能的S种选择重复进行，最后选出S次评测中平均测试误差最小的模型。

留一交叉验证-S折交叉验证的特殊情形是S=N，称为留一交叉验证，往往在数据缺乏的情况下使用，N为给定数据集的容量。

（四）泛化能力

泛化能力：是指由该方法学习到的模型对未知数据的预测能力。

（1）泛化误差：

如果学到的模型是f,那么用这个模型对未知数据预测的误差称为泛化误差。反映了学习方法的泛化能力，如果一个模型具有更小的泛化误差，该模型就更有效。也是所学到的模型的期望风险。

（2）泛化误差上界

性质：它是样本容量的函数，当样本容量增加时，泛化上界趋于0，它是假设空间容量的函数，假设空间容量越大，模型越难学，泛化误差上界就越大。

（五）生成模型与判别模型

监督学习方法又可分为生成方法-生成模型和判别方法-判别模型。

生成方法：由数据学习联合概率分布P（X,Y）,然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型：

  

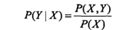
典型的生成模型由：朴素贝叶斯法和隐马尔可夫模型。特点：可还原出联合概率分布，而判别方法不可以；学习收敛速度更快，即当样本容量增加的时候，学到的模型可以更快的收敛于真实模型；当存在隐变量的时候，仍可用生成方法学习，此时判别方法不能用。

判别方法：由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型，即判别模型。判别方法关注于对给的的输入X，应该预测什么样的输出Y。

典型的判别模型：K近邻法、感知器、决策树等。特点：直接学习的是条件概率或决策函数，直接面对预测，往往学习的准确率更高，可以对数据进行各种程度上的抽象、定义特征并使用特征，可简化学习问题。

（六）分类问题

监督学习从数据中学习一个分类模型或分类决策函数，称为分类器（classifier）。分类器对新的输入进行输出的预测，称为分类。可能的输出称为类。类别为多个时，称为多类分类问题。

过程包括学习和分类两个过程，学习过程，根据已知的训练数据集利用有效的学习方法学习一个分类器；分类过程，利用学习的分类器对新的输入实例进行分类。

评价指标：

分类准确率-对于给的的测试数据集，分类器正确分类的样本数与总样本数之比，也就是损失函数是0-1损失时测试数据集上的准确率。

精确率和召回率：关注的类-正类；其他类-负类（二分类为例）

TP:将正类预测为正类数；FN将正类预测为负类数;FP将负类预测为正类数;TN将负类预测为负类数。

精确率：

 

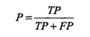
召回率：

 

F1值：精确率和召回率的调和均值。

 

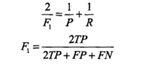
当精确率和召回率都高时，F1值也会高。

常用的统计学习方法：K近邻法、感知器、朴素贝叶斯法、决策树、决策列表、支持向量机、贝叶斯网络、神经网络等。

应用：客户分类模型；非法入侵检测；人脸识别；手写识别；分本分类等。

（七）标注问题

标注（tagging）也是一个监督学习问题，可认为是分类问题的推广，输入是一个观测序列，输出是一个标记序列或状态序列，目的在于学习一个模型，使其可以对观测序列给出标记序列作为预测。

过程分为学习和标注，首先给定一个训练数据集，学习系统基于训练数据集构建一个模型，表示为条件概率分布。标注系统按照学习得到的条件概率分布模型，对新的输入观测序列找到相应的输出标记序列。

评价指标：标注准确率、精确率和召回率。

常用的统计学习方法有：隐马尔可夫模型、条件随机场。

应用：信息抽取（从英文文章中抽取基本名词短语）、自然语言（词性标注）等。

（八）回归问题（Regression）

回归用于预测输入变量（自变量）和输出变量（因变量）之间的关系，回归模型正是表示从输入变量到输出变量之间映射的函数。等价于函数拟合，选择一条函数曲线使其很好拟合已知数据且很好地预测未知数据。

过程有学习和预测，首先给定一个训练数据集，学习系统基于训练数据构建一个模型，最后对新的输入，预测系统根据学习的模型确定相应的输出。

根据输入变量的个数，分为一元回归和多元回归；按输入变量和输出变量之间关系类型即模型的类型，分为线性回归和非线性回归。

常用的损失函数是“平方损失函数”，此时回归问题可由“最小二乘法（least squares）”求解。

可应用于商务领域，例如市场趋势预测、产品质量管理、投资风险分析等。