第八讲 矩阵函数的求法
一、利用Jordan标准形求矩阵函数。
对于矩阵的多项式,我们曾导出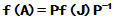 ,
,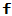 :多项式
:多项式
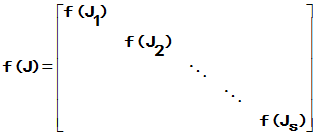
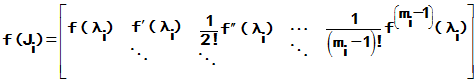
实际上,以上结果不仅对矩阵的多项式成立,对矩阵的幂级数也成立。由此引出矩阵函数的另一种定义及计算方法。
1. 定义:设n阶矩阵A的Jordan标准形为J
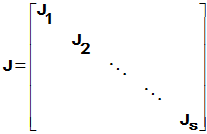 ,
,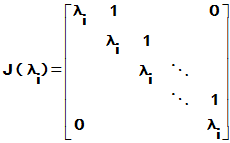
有非奇异矩阵P使得: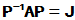
对于函数f(z),若下列函数
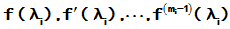
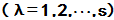
均有意义,则称矩阵函数f(A)有意义,且
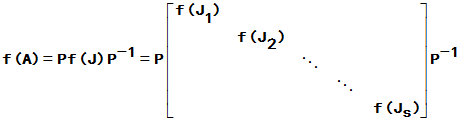
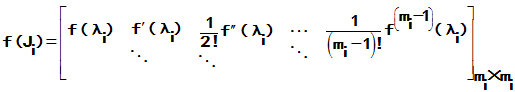 2. 矩阵函数的求法(步骤):
2. 矩阵函数的求法(步骤):
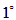 求出A的Jordan标准形及变换矩阵P,
求出A的Jordan标准形及变换矩阵P,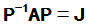
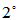 对于J的各Jordan块
对于J的各Jordan块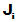 求出
求出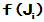 ,即计算出
,即计算出
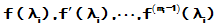
并按照顺序构成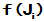 ,
,
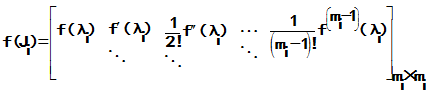
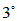 合成
合成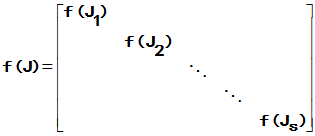
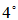 矩阵乘积给出
矩阵乘积给出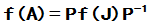
需要说明的是,计算结果与Jordan标准形中Jordan块的顺序无关。
例1 (教材P176例3-8). 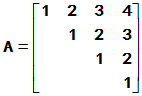 ,求
,求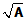
[解] 1 求出J及P
求出J及P
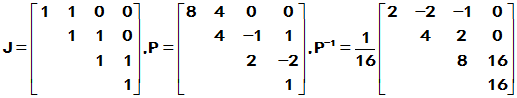
2 求出
求出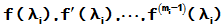 并构成
并构成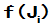 :
:
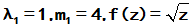
f(1)=1,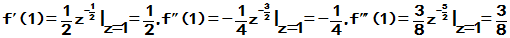

3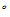 合成
合成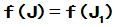
4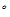 求
求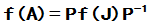 ,
,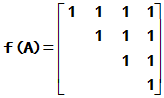
说明:
(1)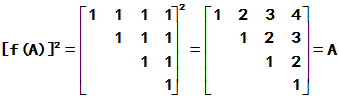 ,
,
可见这样的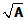 确与
确与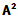 构成反函数;
构成反函数;
(2)矩阵函数的种类不仅是我们介绍的这种,如辛矩阵。以
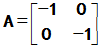 为例,以我们这里的定义,
为例,以我们这里的定义,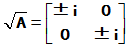 ,但
,但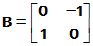
亦满足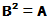 ,即B也可以看作某种
,即B也可以看作某种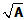
二、利用零化多项式求解矩阵函数.
利用Jordan标准型求解矩阵函数的方法比较复杂,它需要求J
和P。下面我们介绍根据零化多项式求解矩阵函数的一种方法。
定律:n阶方阵A的最小多项式等于它的特征矩阵的第n个(也就是最后一个)不变因子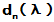 。(可参见张远达《线性代数原理》P215)
。(可参见张远达《线性代数原理》P215)
设n阶方阵A的不变因子反向依次为
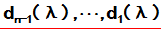 ,由它们给出的初等因子分别为
,由它们给出的初等因子分别为
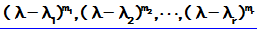 ;
; ;
;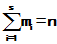
由于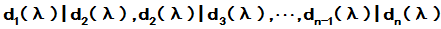 ,故
,故
1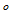
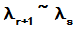 必定出现在
必定出现在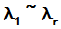 中;
中;
2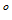 若
若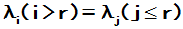 则
则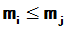
根据上述定理,A的最小多项式
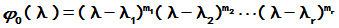
A的最小多项式为其零化多项式,
即 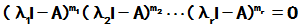
令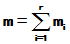 ,则可见
,则可见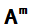 可以由
可以由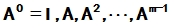 线性表示,从而
线性表示,从而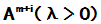 亦可由
亦可由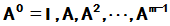 线性表示。所以,矩阵函数f(A)若存在,也必定可由
线性表示。所以,矩阵函数f(A)若存在,也必定可由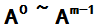 线性表示。
线性表示。
因此,我们定义一个系数待定的(m-1)次多项式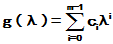 ,根据以上论述,适当选择系数
,根据以上论述,适当选择系数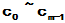 ,就可以使f(A)=g(A).
,就可以使f(A)=g(A).
又,假设J,P分别为A的Jordan标准形及相应变换矩阵: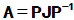
则
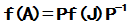 ,
,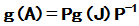
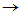 f(J)=g(J)
f(J)=g(J)
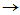
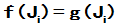
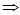
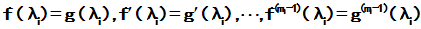
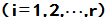
由于g(A)为待定系数的多项式,上面就成为关于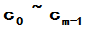 的线性方程组。且方程的个数为
的线性方程组。且方程的个数为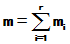 等于未知数个数,正好可以确定
等于未知数个数,正好可以确定
由此给出根据最小多项式求矩阵函数的一般方法。
1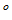 求出最小多项式
求出最小多项式
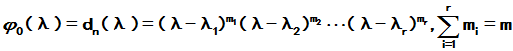 ;
;
(或者特征多项式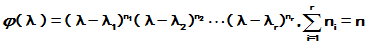 )
)
2 形式上写出待定多项式
形式上写出待定多项式
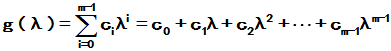
(或者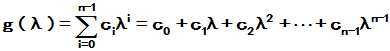 )
)
3 求解关于
求解关于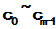 的线性方程组
的线性方程组
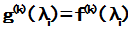
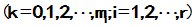
(或者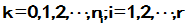 )
)
4 求出g(A),即可得f(A)=g(A).
求出g(A),即可得f(A)=g(A).
从推导的过程看,似乎不仅最小多项式可用于矩阵函数的计算,一般的零化多项式也可以,其中以特征多项式最为方便。
例2. 采用新方法计算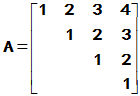 的函数
的函数 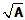 。(
。(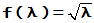 )
)
[解] 1
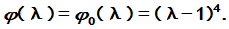
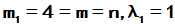 ;
;
2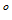
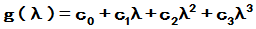
3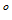 方程组为
方程组为
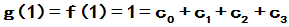
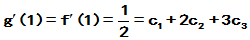
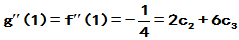

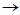
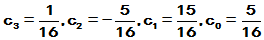
4
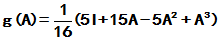
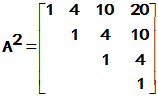 ,
,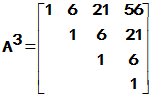
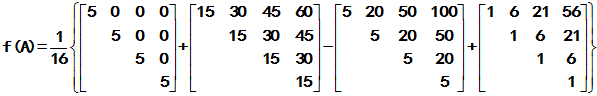
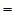

与Jordan标准形方法完全一致。
作业: P163 6




 浙公网安备 33010602011771号
浙公网安备 33010602011771号