§8 平面束与平面把
一 平面束:
1定义:空间中过一定直线 的所有平面的集合称为有轴平面束,
的所有平面的集合称为有轴平面束,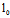 称为这平面束的轴;空间中平行于一定平面的所有平面的集合称为平行平面束。
称为这平面束的轴;空间中平行于一定平面的所有平面的集合称为平行平面束。
有轴、平行平面束统称为平面束。
2 方程:
定理1:对任一对确定的不全为0的实数λ,μ,方程
λ( x+
x+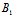 y+
y+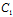 z+
z+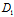 )+μ(
)+μ( x+
x+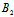 y+
y+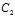 z+
z+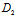 )=0 (1)
)=0 (1)
表示过二相交平面
 :
: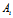 x+
x+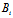 y+
y+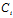 z+
z+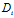 =0 , i=1,2
=0 , i=1,2
的交线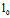 的一个平面;反之,对过
的一个平面;反之,对过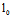 的任一平面π,必存在不全为0的实数λ,μ,使π的方程为(1)
的任一平面π,必存在不全为0的实数λ,μ,使π的方程为(1)
证明:先证(1)表示过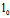 的平面。
的平面。
(1)即为(λ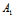 +μ
+μ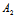 )x+(λ
)x+(λ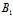 +μ
+μ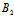 )y+(λ
)y+(λ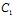 +μ
+μ )z+λ
)z+λ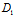 +μ
+μ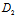 =0
=0
我们断言:上式中x,y,z的系数不全为0,其实若不然,则有
-μ:λ= :
: =
=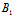 :
: =
=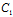 :
: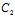
这与 与
与 相交矛盾 ∴(1)表示一平面π,又显然π过
相交矛盾 ∴(1)表示一平面π,又显然π过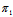 与
与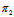 的交线l。
的交线l。
次证:对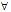 过
过 的平面π,必存在不全为0的λ,μ,使π的方程为(1)
的平面π,必存在不全为0的λ,μ,使π的方程为(1)
首先,若π≡ ,取λ=1,μ=0,若π≡
,取λ=1,μ=0,若π≡ ,取λ=0,μ=1,
,取λ=0,μ=1,
一般地,若π≠ ,i=1,2 取π上一点A(α,β,γ)
,i=1,2 取π上一点A(α,β,γ)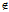 l。
l。
于是,( α+
α+ β+
β+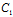 γ+
γ+ )(
)( α+
α+ β+
β+ γ+
γ+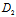 )=0
)=0
即 λ:μ=-(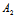 α+
α+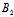 β+
β+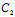 γ+
γ+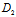 ):(
):( α+
α+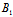 β+
β+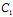 γ+
γ+ )
)
不妨取 λ=-( α+
α+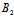 β+
β+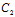 γ+
γ+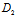 ),μ=
),μ=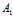 α+
α+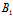 β+
β+ γ+
γ+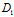
则 (1)便表示过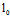 的平面,又显示该平面过A,∴这平面就是π
的平面,又显示该平面过A,∴这平面就是π
例:求过二平面4x-y+3z-1=0与x+5y-z+2=0的交线,且过原点的平面的方程
解:略。
定理2:设在方程(1)中, ∥
∥ ,则对任意一对满足-μ:λ≠
,则对任意一对满足-μ:λ≠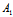 :
: 的不全为0的实数λ,μ,(1)表示平行于
的不全为0的实数λ,μ,(1)表示平行于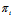 的一个平面π;反之,对任意平行于
的一个平面π;反之,对任意平行于 的平面π,必存在满足-μ:λ≠
的平面π,必存在满足-μ:λ≠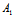 :
: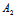 的不全为0的实数λ,μ,使π的方程为(1)
的不全为0的实数λ,μ,使π的方程为(1)
证明:先证,对任意一对满足-μ:λ≠ :
: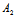 的不全为0的实数λ,μ(1)
的不全为0的实数λ,μ(1)
表示平行于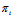 的平面π。
的平面π。
由于-μ:λ≠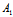 :
: , ∴λ
, ∴λ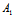 +μ
+μ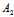 ≠0,从而
≠0,从而
(1)表示一平面π,又
 :
: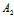 =
=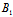 :
: =
= :
: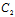 =k
=k
则(λ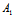 +μ
+μ ):
): =(λ
=(λ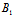 +μ
+μ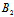 ):
): =(λ
=(λ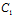 +μ
+μ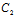 ):
): =λk+μ
=λk+μ
∴π∥ ∥
∥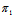
再证:对任意平行于 的平面π,必存在不全为0的且满足
的平面π,必存在不全为0的且满足
-μ:λ≠ :
: 的λ,μ,使π的方程为(1)
的λ,μ,使π的方程为(1)
首先,若π≡ ,取λ=1,μ=0;若π≡
,取λ=1,μ=0;若π≡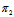 ,取λ=0,μ=1显然此时
,取λ=0,μ=1显然此时
-μ:λ≠ :
: (
( ,
,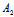 要么同时为0,要么同时非0)
要么同时为0,要么同时非0)
一般地,若π≠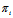 ,i=1,2 取π上一点A(α,β,γ)
,i=1,2 取π上一点A(α,β,γ)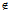 π,同定理1的证明类似。取λ,μ满足
π,同定理1的证明类似。取λ,μ满足
λ:μ=-(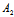 α+
α+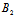 β+
β+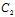 γ+
γ+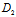 ):(
):(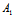 α+
α+ β+
β+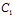 γ+
γ+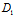 )
)
今验证 -μ:λ≠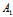 :
: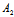 其实,若不然,则
其实,若不然,则
(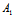 α+
α+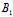 β+
β+ γ+
γ+ ):(
):( α+
α+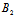 β+
β+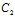 γ+
γ+ )=
)=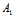 :
:
即 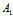 (
(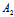 α+
α+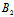 β+
β+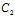 γ+
γ+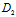 )-
)-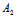 (
( α+
α+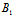 β+
β+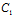 γ+
γ+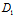 )=0
)=0
(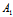
 -
-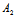
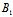 )β+(
)β+(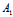
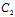 -
-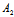
 )γ+
)γ+
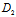 -
-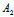
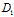 =0
=0
而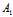 :
: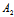 =
=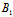 :
: =
=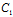 :
: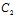 ∴
∴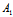 :
: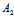 =
= :
: ∴
∴ ≡
≡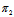
这与已知不符, ∴-μ:μ≠ :
: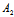 ,即(1)表示一平行于
,即(1)表示一平行于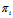 的平面,
的平面,
又显然A(α,β,γ)在该平面上, ∴这平面正是π
定理3:设平面π:Ax+By+Cz+D=0,则π′∥π〈═〉π′的方程可表为
Ax+By+Cz+Dλ=0
事实上,"〈═"显然
"═〉"若π′∥π,且设π′:A′x+B′y+C′z+D′=0
则 A′:A=B′:B=C′:C=k
∴π′:kAx+kBy+kCz+D′=0
即 π′:Ax+By+Cz+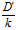 =0
=0
例:求与平面3x+y-z+4=0平行,且在z轴的截距等于-2的平面的方程。
解:略。
二 平面地(平面汇)
1、定义:空间中过一定点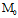 的所有平面的集合称为平面把,
的所有平面的集合称为平面把,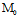 ——把心
——把心
2、方程:
定理1:对于任意不全为0的A,B,C,方程
A(x-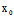 )+B(y-
)+B(y- )+C(z-
)+C(z-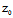 )=0 (2)
)=0 (2)
表示过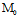 (
(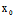 ,
,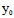 ,
, )的一个平面π,反之,对过
)的一个平面π,反之,对过 的任一平面π必存在不全为0的A,B,C,使其方程为 (2)
的任一平面π必存在不全为0的A,B,C,使其方程为 (2)
更一般地,我们有
定理2:对任意不全为0的λ,μ,ν,方程
λ(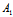 x+
x+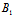 y+
y+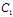 z+
z+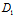 )+μ(
)+μ( x+
x+ y+
y+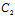 z+
z+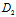 )+ν(
)+ν( x+
x+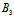 y+
y+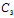 z+
z+ )
)
=0 (3)
表示过三平面  :
: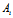 x+
x+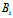 y+
y+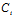 z+
z+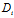 =0, i=1,2,3
=0, i=1,2,3
(唯一)交点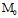 (
(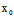 ,
,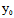 ,
,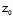 )的一个平面π;反之,对任意过
)的一个平面π;反之,对任意过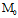 的平面π,必存在不全为0的λ,μ,ν,使π的方程为(3)。
的平面π,必存在不全为0的λ,μ,ν,使π的方程为(3)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号