§2 矢量的加减法
一 矢量的加法:
定义1 设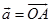 、
、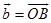 ,以
,以 与
与 为边作一平行四边形
为边作一平行四边形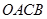 ,取对角线矢量
,取对角线矢量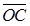 ,记
,记 ,如图1-3,称
,如图1-3,称 为
为 与
与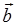 之和,并记作
之和,并记作
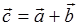
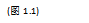

这种用平行四边形的对角线矢量来规定两个矢量之和的方法称作矢量加法的平行四边形法则.
如果矢量 与矢量
与矢量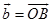 在同一直线上,那么,规定它们的和是这样一个矢量:
在同一直线上,那么,规定它们的和是这样一个矢量:
若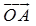 与
与 的指向相同时,和向量的方向与原来两矢量相同,其模等于两矢量的模之和(图1-4).
的指向相同时,和向量的方向与原来两矢量相同,其模等于两矢量的模之和(图1-4).


若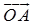 与
与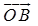 的指向相反时,和矢量的模等于两矢量的模之差,其方向与模值大的矢量方向一致(图1-5).
的指向相反时,和矢量的模等于两矢量的模之差,其方向与模值大的矢量方向一致(图1-5).


由于平行四边形的对边平行且相等,可以这样来作出两矢量的和矢量:
定义2 作 ,以
,以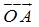 的终点为起点作
的终点为起点作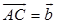 ,联接
,联接 (图1-6)得
(图1-6)得
 . (1.2-1)
. (1.2-1)
该方法称作矢量加法的三角形法则.
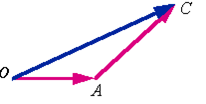
矢量加法的三角形法则的实质是:
将两矢量的首尾相联,则一矢量的首与另一矢量的尾的连线就是两矢量的和矢量.
据矢量的加法的定义,可以证明矢量加法具有下列运算规律:
定理 矢量的加法满足下面的运算律:
1、交换律 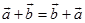 , (1.2-2)
, (1.2-2)
2、结合律  . (1.2-3)
. (1.2-3)
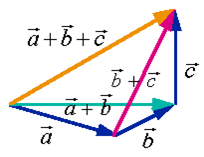
证 交换律的证明从矢量的加法定义即可得证,结合律的证明从图1-7可得证.

二 矢量的减法
定义3 若 ,则我们把
,则我们把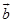 叫做
叫做 与
与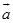 的差,记为
的差,记为
显然, 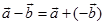 ,
,
特别地,  .
.
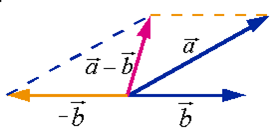
由三角形法则可看出:要从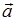 减去
减去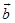 ,只要把与
,只要把与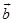 长度相同而方向相反的矢量
长度相同而方向相反的矢量 加到矢量
加到矢量 上去.由平行四边形法则,可如下作出矢量
上去.由平行四边形法则,可如下作出矢量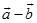 (图1-8).
(图1-8).

例1 设互不共线的三矢量 、
、 与
与 ,试证明顺次将它们的终点与始点相连而成一个三角形的充要条件是它们的和是零矢量.
,试证明顺次将它们的终点与始点相连而成一个三角形的充要条件是它们的和是零矢量.
 证 必要性 设三矢量
证 必要性 设三矢量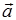 、
、 、
、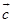 可以构成三角形
可以构成三角形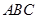 (图1-9),
(图1-9),
即有
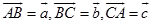 ,
,
那么, 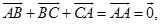
即 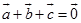 .
.
充分性 设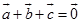 ,作
,作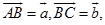 那么
那么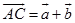 ,所以
,所以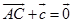 ,从而
,从而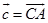 ,所以
,所以 、
、 、
、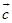 可以构成三角形
可以构成三角形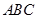 .
.
例2 用矢量法证明:对角线互相平分的四边形是平行四边形.
证 设四边形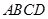 的对角线
的对角线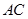 、
、

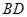 交于
交于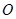 点且互相平分(图1-10)
点且互相平分(图1-10)
因此从图可看出:
 ,
,
所以,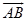 ∥
∥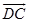 ,且
,且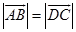 ,
,
即四边形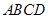 为平行四边形.
为平行四边形.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号