三. 空间域灰度变换

三. 空间域灰度变换

作用：是图像增强的一个方向，目的是通过一定的操作，实现对图像的某些特征的增强。此外还有空间滤波、频率域滤波等操作，放在后面讲。

3.1 直接灰度变换

作用：可调整图像的灰度动态范围或图像对比度。

3.1.1 线性变换

目的：通过线性变换讲图像的灰度值范围拉伸到指定范围：

公式：

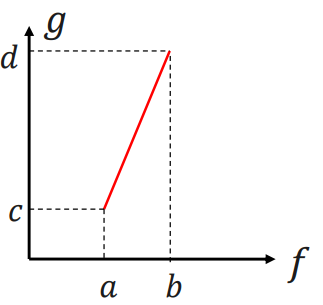
将\(f(x,y)\)变换为\(g(x,y)\)，灰度范围从\([a,b]\)映射到\([c,d]\)：

\[g(x,y)=c+\frac{d-c}{b-a}(f(x,y)-a) \tag{1} \]

我们令\(k=\frac{d-c}{b-a}\)，那么根据k的取值，我们得到以下应用场景：

• k>1：灰度区间扩大。可以改善曝光程度不足的情况。
• k=1：灰度区间大小不变，灰度值整体平移。
• 0<k<1：灰度区间变窄。
• k<0：图像的灰度值发生反转，亮的变暗，暗的变亮。当k=-1时，图像完全取反。

应用

在曝光不足的情况下，图像灰度局限在很小的一个区间内，因此可以通过线性变换或拉伸进行改进。

3.1.2 分段线性变换

目的：突出感兴趣的灰度区间，抑制不感兴趣的灰度区间。

公式：

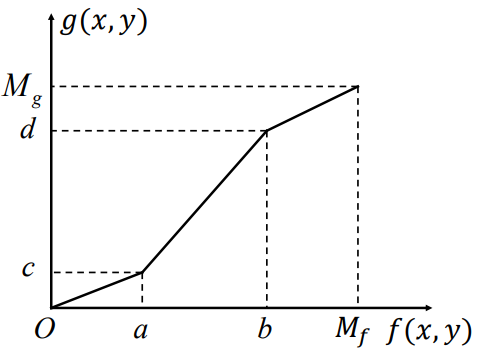
\(f(x,y)\)灰度范围为\([0,M_f]\)，将感兴趣的灰度区域\([a,b]\)拉伸到\([c,d]\)，得到变换后的图像\(g(x,y)[0,M_g]\)：

\[g(x,y)= \begin{cases} \frac{c}{a}f(x,y),\quad 0\leq f(x,y)<a \\ \frac{d-c}{b-a}(f(x,y)-a)+c,\quad a\leq f(x,y)<b \\ \frac{M_g-d}{M_f-b}(f(x,y)-b)+d,\quad b\leq f(x,y)\leq b \end{cases} \tag{2} \]

简单来说，就是分区域进行三次线性变换。

3.1.3 非线性变换

将灰度值按照统一的变换函数进行变换，函数是非线性的，常用的有对数函数变换和指数函数变换两种形式。

• 对数函数变换：

  • 公式如下：

    原图像\(r=f(x,y)\)，变换后的图像\(s=g(x,y)\)，那么：

    \[s=c\log{(1+r)} \tag{3} \]

    c用来调整图像s的区间，r加上1是为了避免灰度出现负数。

  • 效果：

    因为对数的特点，变化后低灰度区得到扩展，高灰度区域得到压缩。

  • EG：现有一个图像的傅里叶变换频谱范围为\([0,10^6]\)，显然无法直接绘图，可以使用对数变换，然后再绘制。

• 指数函数变换：

  • 公式如下：

    原图像\(r=f(x,y)\)，变换后的图像\(s=g(x,y)\)，那么

    \[s=cr^{\gamma} \tag{4} \]

    \(\gamma\)<1时：灰度级得到提升，图像变亮。

    \(\gamma\)>1：灰度级降低，图像变暗。

3.2 直方图修正

3.2.1 概述

灰度直方图：横坐标为像素灰度级，纵坐标为灰度出现频率，反映了图像的灰度分布情况，其中频率\(p_i\)的公式为：

\[p_i=\frac{n_i}{n} \tag{5} \]

其中：n为图像的像素数量，\(n_i\)为图像中灰度值为i的个数。

性质：

• 只能反映灰度分布情况，不能反应像素的位置。
• 一幅图像对应唯一的直方图，反之不成立。

基于灰度直方图的图像增强技术包括直方图均衡化和直方图规范化。

3.2.2 直方图均衡化

思路：通过某种变换，将原图像变成一副灰度直方图为均匀分布的新图像。变换后图像的直方图变成平直的。

效果：增加像素灰度值的动态范围，从而达到增强图像整体对比度的效果。

公式推导：

假设\(r\)为归一化的原图像，\(s\)为经直方图修正后的灰度图像，二者的范围均为【0,1】，有函数使得：

\[s=T(r) \tag{6} \]

对函数要求如下：

• \(T(r)\)单调递增。这是为了保证黑白的次序不发生颠倒。
• 变化前和变化后都属于【0,1】，确保变化前后像素灰度值动态统一。

同时存在反函数，使得：

\[s=T^{-1}(r) \tag{7} \]

该函数也存在上述两点要求。

• 连续型像素：

  假设变量r的概率密度函数为\(p_r(r)\)，而s的概率密度函数为\(p_s(s)\)，显然，s是关于r的函数值，又因为映射函数\(s=T(r)\)单调递增且范围一致，因此存在s的分布函数为：

  \[F_s(s)=\int_{-\infty}^sp_s(s)ds=\int_{-\infty}^rp_r(r)dr \tag{8} \]

  对上式求导，得到变换后s的概率密度函数：

  \[p_s(s)=\frac{dF_s(s)}{ds}=\frac{d[\int_{-\infty}^rp_r(r)dr]}{ds}=p_r(r)\frac{dr}{ds}=p_r(r)\frac{dr}{d[T(r)]} \tag{9} \]

  由公式九可知：我们可以通过改变变换公式\(T(r)\)来控制改变后图像灰度级的概率密度函数，从而改善图像的灰度层次。

  进一步的，由于人的视觉特性，人们对于均匀分布的灰度直方图构成的图像观感更好，因此\(p_s(s)\)最好是均匀分布密度函数。由概率论可得：在[a,b]区间均匀分布，密度函数为\(\frac{1}{b-a}\)，因为我们实现对灰度进行了归一化，灰度范围变为了[0,1]，因此密度函数为：

  \[p_s(s)=1 \tag{10} \]

  代入公式9，可以得到：

  \[\begin{align*} p_s(s)=p_r(r)\frac{dr}{ds} \\ p_s(s)ds=p_r(r)dr \\ 因为：p_s(s)=1 \\ 所以：ds=p_r(r)dr \end{align*} \tag{11} \]

  对公式11求积分，最终得到：

  \[s=T_r(r)=\int_0^r{p_r(r)}dr \tag{12} \]

• 离散型像素：

  对公式12进行离散化，得到公式如下：

  \[s=T_r(r)=\sum_{i=0}^kp_r(r_i)=\sum_{i=0}^k\frac{n_i}{n} \tag{13} \]

  注意：上述像素均进行了归一化。

  EG：均衡化下述图像（假设图像的灰度级为[0,9]）：

  

  解：

  1. 计算原始图像灰度分布频率：

  \[p_r(r_i)=\frac{n_i}{n}=[3/25,2/25,4/25,4/25,1/25,1/25,4/25,1/25,2/25,3/25] \]

  2. 计算原始图像累计分布频率：

  \[s=T_r(r)=\sum_{i=1}^\frac{n_i}{n}=[3/25,5/25,9/25,13/25,14/25,15/25,19/25,20/25,22/25,25/25] \]

  3. 将像素范围变换回【0,9】：

  \[s'=(9-0)s+0=9s=[1.08,1.8,3.24,4.68,5.04,5.4,6.84,7.2,7.92,9] \]

  4. 对s'取证，按照四舍五入的方法，得到的s''为：

  \[s''=[1,2,3,5,5,5,7,7,8,9] \]

  5. 按照映射关系，对原始图像进行改造：

  例如：原本\(image[0][0]=1\)，在\(p_r(r_i)\)中位于下标为1的位置，像素变换并取整后为2.

  所以：我们观察\(s''\)即可，所有原本灰度为0的变为1，为1的变为2，为2的变为3，为3、4、5的变为5，为6、7的变为7，为8的变为8，为9的变为9。得到新图像如下：

  \[\begin{matrix} 2&5&9&9&8 \\ 3&2&5&7&5 \\ 5&7&1&7&5 \\ 7&8&3&1&5 \\ 3&9&3&7&1 \end{matrix} \]

  通过上例我们可以看出：实际上直方图均衡化是将出现频率较低且灰度值较为接近的像素的灰度值转化为统一灰度值，表现在灰度直方图上就是灰度图直方图上就是突出的柱子明显减少。

缺点：

如果一幅图像整体偏暗或者偏亮，那么直方图均衡化的方法很适用。但直方图均衡化是一种全局处理方式，它对处理的数据不加选择，可能会增加背景干扰信息的对比度并且降低有用信号的对比度（如果图像某些区域对比度很好，而另一些区域对比度不好，那采用直方图均衡化就不一定适用）。此外，均衡化后图像的灰度级减少，某些细节将会消失；某些图像（如直方图有高峰），经过均衡化后对比度不自然的过分增强。针对直方图均衡化的缺点，已经有局部的直方图均衡化方法出现。

3.2.3 直方图规定化

目的：修改一幅图的直方图，使其与另一幅图像的直方图匹配或具有一种规定形状的直方图的增强方法。是直方图均衡化的一种特例。

步骤：

假设已归一化的原始图像的概率密度函数为\(p_r(r)\)，已经归一化的希望得到的目标图像的概率密度函数为\(p_z(z)\)

1. 对原始图像进行直方图均衡化处理：

   \[s_k=T(r_k)=\sum_{i=0}^kp_r(r_i) \tag{14} \]

2. 对目标图像进行直方图均衡化处理：

   \[v_j=G(z_j)=\sum_{l=0}^jp_z(z_l) \tag{15} \]

3. 根据公式15，得到逆向变换：

   \[z=G^{-1}(v) \tag{16} \]

   也就意味着可以使用均衡化后的灰度级v得到目标函数的灰度级z。

4. 因为对\(p_r(r)\)和\(p_z(z)\)进行了均衡化处理，所以二者具有相同的概率密度函数，因此可以使用s代替公式16中的v，得到：

   \[z=G^{-1}(s) \]

   也就是说：可以使用原始图像均衡化的后的灰度值s来求目标图像的灰度级z。

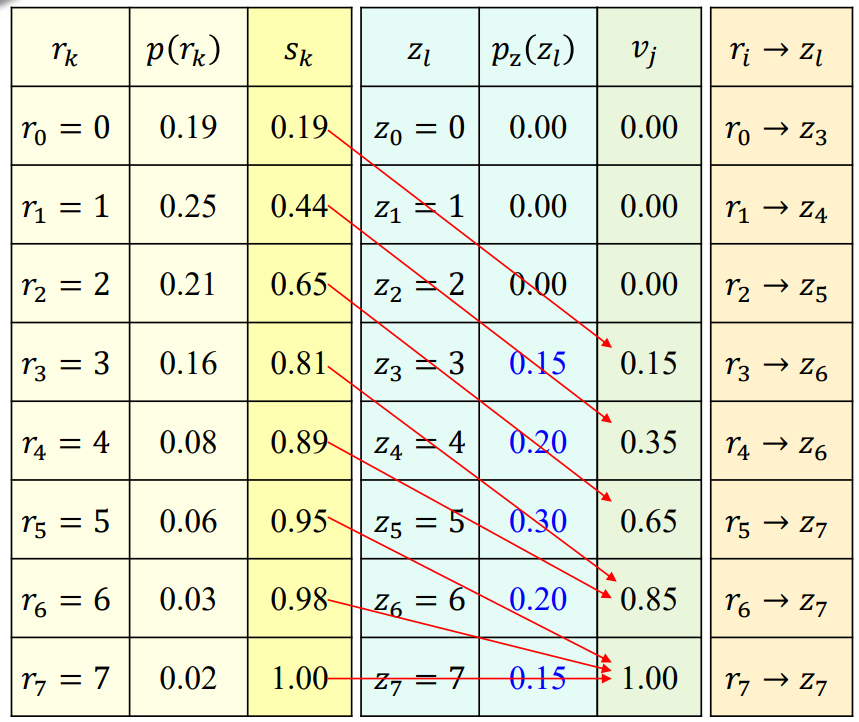
5. 在灰度离散的情况下，依\(v_j\rightarrow s_k\)（两幅图的均衡化后的灰度）的最靠近原则，进行\(r_i \rightarrow z_l\)的变换。

看不懂没关系，下面看实例：

EG:

假设现有原始图像，规格为64*64，有8级灰度，灰度分布如下：

\(r_k\)(灰度值)	\(n_k\)(出现的次数)
0	790
1	1023
2	850
3	656
4	329
5	245
6	122
7	81

目标图像的灰度分布如下：

\(z_k\)(目标图像的灰度)	\(p_z(z_k)\)(出现的频率)
0	0
1	0
2	0
3	0.15
4	0.2
5	0.3
6	0.2
7	0.15

请计算出直方图规定化后的图像：

解答如下：

1. 原始图像直方图均衡化：

2. 计算原始图像归一化后的概率密度函数：

\[ p_r(r_k)=\frac{n_k}{n}=\{0.19,0.25,0.21,0.16,0.08,0.06,0.03,0.02\} \]

1. 计算直方图均衡化后的分布函数：

\[ s_k=\sum_{i=0}^kp_r(r_i)=\{0.19,0.44,0.65,0.81,0.89,0.95,0.98,1.00\} \]

2. 图像直方图均衡化后：

因为概率密度函数题目中已经给出，因此这里仅计算分布函数：

\[ v_j=\sum_{j=0}^kp_z(z_j)=\{0,0,0,0.15,0.35,0.65,0.85,1.00\} \]

3. 按照直方图均衡化后得到的\(s_k,v_j\)，建立原图像-->目标图像的映射关系，具体方式为：最靠近原则，即哪一个\(v_j\)和\(s_k\)的差值最小，那么相应的\(r_k\)就映射到目标图像的\(z_j\)：

\[ s_0=0.19 \\ v_3<s_0<v_4,且：\\ |s_0-v_3|<|s_0-v_4| \\ 因此：v_3和s_0距离最近，符合最靠近原则，相应的 \\ r_0 \rightarrow z_3的映射成立。 \\ 其它的也这么算，得到映射如下 \]

4. 求新生成图像的概率密度函数：

因为新图像是由原始图像映射而来，且两个图像的像素总数不变，且二者存在映射关系。因此，对于\(r_i\rightarrow z_l\)，使得\(p_z(z_l)=p_r(r_i)\)，因此我们可以计算出如下数据：

\[ \begin{align*} p_z(z_l)&=\{0,0,0,0.19,0.25,0.21,0.16+0.08,0.06+0.03+0.02\} \\ &=\{0,0,0,0.19,0.25,0.21,0.24,0.11\} \end{align*} \]

5. 最终变换效果如下：

思考：

1. 为什么在进行最靠近原则时选取的度量标准是分布函数而不是概率密度按函数：

   显然，我们在映射时，希望原本灰度值较高的映射后灰度值也较高，较低的映射后也较低，也就是避免映射导致黑白逆转。概率密度函数仅包含灰度出现频率的信息，而不包含灰度的大小分布顺序，以此为标准因此很可能出现灰度的黑白颠倒的情况。而分布函数包含了这两种信息，因此可以较大程度上避免出现黑白逆转的乌龙事件。

3.3 图像的代数运算

略。