BUAA-OO-Unit1总结
1.1 思路
1.1.1最初的想法
简单划分为Expr、Term、Factor三个层次,对每个层次建立一个类,实例化计算接口,对字符串做递归下降,失败 -> 忽视了表达式也可以是一种因子的逻辑关系,构建合并化简方法困难。
1.1.2 重构
参考Training范例及讨论区,建立Factor接口,对每种Factor单独建类实例化接口;将计算方法打包建成Poly类。Expr是Term的"叠加",Term是Factor的"累积",Factor是一个或多个基元ax^b的"叠加"。
1.1.3 合并
希望可以获得尽可能简洁的形式。
ax^b的形式最简洁了。考虑Term能否化简成该形式。若Term可以化成ax^b的形式,则Expr就是\Sigma ax^b,则Factor是ax^b或\Sigma ax^b,若Term中出现一个\Sigma ax^b的Factor,那么Term就不能保证一定可以化简成ax^b的形式。由上知Expr显然不可能。所以必须接受Term是\Sigma ax^b,这样Expr也是\Sigma ax^b,Factor可以是ax^b或\Sigma ax^b,这样Factor的乘积Term依然可以化简成\Sigma ax^b。
接下来构建对应的合并与化简方法即可,主要包括:将三个层次类分别转化成Poly(赋予计算能力),写Poly(ax^b转化而来)之间的乘法mult和ArrayList<Poly>(\Sigma ax^b转化而来)的加法plus和乘法mult,以及对ArrayList<Poly>去重化简的unique方法。每次计算后,都要进行一次unique来避免化简不彻底对后续计算产生的不便。
感谢强生同学在讨论区的分享,让我少走了很多弯路。
unique方法只涉及同类项的合并。只要将ArrayList<Poly>中的元素取出,String s = "x**"+poly.getExp()当Key、元素本身做Value,放入HashMap<String, Poly>中,边放边合并同Key的Value即可。这里,使用不可变对象String做Key是一种比较安全的偷懒做法,在之后的作业里有部分同学使用了HashMap<Factor>做Key,需要重写equals、hashCode方法。但是用String有小瑕疵,我们会在后面看到。
1.1.4 连续符号的处理
出于对正则的厌恶,预处理仅去掉了空白字符,未对多个-+相邻的情况做处理。因而在parse时遇到了困难:表达式的符号性如何传递?
注意到递归下降实际上构建出了一棵以Factor为叶节点、Term和Expr为分支节点的表达式树,且本层的负号仅影响下一层的节点,想到线段树lazy标记。通俗的想法是:一方面,在本层级检测下一级的符号,若为 '-' 则将下一级isNegative置1;另一方面,若本级isNegative标记为1,则仅在需要返回上级时将下层基元全部取反。具体操作,如下图所示:

画起来太麻烦了,直接放代码吧
public boolean checkPosNeg(boolean isNegative) {
if (lexer.peek().equals("-")) {
lexer.next();
return !isNegative;
}
if (lexer.peek().equals("+")) {
lexer.next();
}
return isNegative;
}
public Expr parseExpr(boolean isNegative) throws Exception {
Expr expr = new Expr();
if (lexer.checkPrePosMinToken()) {
expr.addTerm(parseTerm(checkPosNeg(false)));
} else {
expr.addTerm(parseTerm(false));
}
while (lexer.peek().equals("+") || lexer.peek().equals("-")) {
expr.addTerm(parseTerm(checkPosNeg(false)));
}
expr.setPolys(Poly.unique(expr.polynize()));
if (isNegative) {
expr.negate();
}
return expr;
}
public Term parseTerm(boolean isNegative) throws Exception {
Term term = new Term();
term.addFactor(parseFactor(checkPosNeg(false)));
while (lexer.peek().equals("*")) {
lexer.next();
term.addFactor(parseFactor(false));
}
term.setPolys(Poly.unique(term.polynize()));
if (isNegative) {
term.negate();
}
return term;
}
parseFactor类似,比较长放不下。
1.1.5 输出
由于将Expr视作Term的加法,故可能出现x+-x^2+x^3这种情况,虽符合题目要求,但不够简洁——输出结果前消去多余的+即可(向正则低头)。
1.1.6 小困惑
遗留下了一个困惑:Number、Power、Expr都“是”一种Factor,为什么选择Factor接口而不是Factor抽象类?
2 hw2
2.1 任务
支持自定义函数、求和函数、三角函数。
2.2 实现
2.2.1 三角函数
先从三角函数入手,因为自定义函数、求和函数都与三角函数有关联。
加入三角函数Triangle后,此时的数学基元应当是ax^b\Pi sin(factor)cos(factor) 。
Triangle本身自带四个属性:type、factor、exp、negative。
| type | factor | exp | negative |
|---|---|---|---|
| sin OR cos | Factor类型 | 指数 | 标注符号 |
对Triangle建模后,相应地完善Poly计算方法和化简方法即可。值得一提的,由于某种神秘力量HashMap自动按Key的hash值对entry排了序,存储三角函数的HashMap也不例外;所以加上Triangle的基元依然可以利用字符串来去重、合并——只需要遍历基元Poly的三角函数容器,拼接到x**后面即可得Key。现在让我们来填上前面埋的坑:测试中发现极少数情况下,合并失效,如样例sin(x**2)*cos(x**2)-sin(x)+cos(x**2)*sin(x**2)会被原样输出。猜测与HashMap扩容时会反向存储有关,而运行和调试的初始容量并不相同。
2.2.2 自定义函数和求和函数
创建FuncFactory,表达式中遇到函数就扔到里面,拿出处理好的表达式。这里借鉴了研讨课同组石子瑄同学的思路,特此致谢。具体实现中,分别建立自定义函数和求和函数的内部类即可。
工厂内部:原始表达式字符串 ==> 做了字符串替换后的表达式串 ==> parseExpr。
为了预防可能的迭代,架构支持各种函数名、各种参数名和参数个数的自定义函数,也可应对sum套sum的情况。
2.3 容易踩坑的点
一是实参的代入顺序。对三个形参分别replaceAll容易导致刚把形参y全换成实参x**2,接着又把x全部换成x**2。我的办法是手工正则匹配[param1|param2|...|paramn],边遍历边做实参代换,只扫一遍表达式。(再次向正则低头)
二是sum解析中正则错误地将所有的变元i全部换成数字,产生"sin(x) --> s1n(x)"的bug。稳妥的做法依然是手工匹配,在Lexer类中写入对循环自变量的检测即可。
3 hw3
本来以为是一次可以摆了的作业,看一眼指导书,发现三角函数里面只能是"因子"……也就是说,如果里面是个表达式,还需要额外加一层括号把它包起来。
经过化简,三角函数的因子只可能是以下四类:Number,Power,Triangle和Expr,在toString前检测下里面到底是个什么东西就行了。我的做法是分别把里面当做前三类parse一下试试看,如果均产生异常,那么就是Expr了,给它加上括号。
这里我陷入了面向过程的误区,用了try...catch结构的嵌套来省时间,导致圈复杂度上去了,而且可能只有原作者能看懂在干什么,不利于团队开发及维护。如果用三个boolean值对三次独立try...catch的结果进行标记,再位运算,应该更“面向对象”一些。
4 基于度量的分析
Metrics
借助了idea插件MetricsReloaded。
由于三次作业架构保持了连续性,所以直接放最后一次的吧。
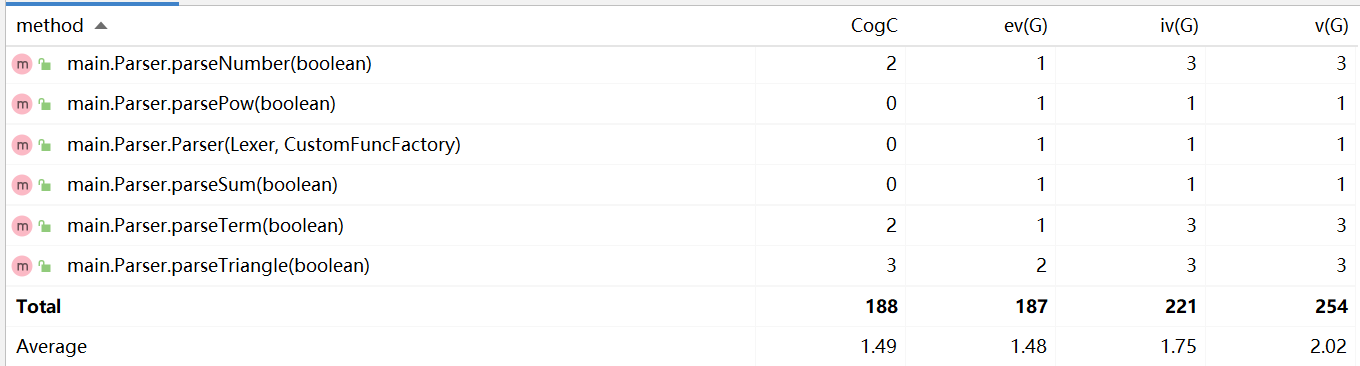
图1 method分析
方法的平均CogC、ev(G)、iv(G)、v(G)都比较低,体现了高内聚低耦合的设计思想。

图2 class的分析
Parser、Poly、SigmaFunctory类的OCavg(平均圈复杂度)和WMC(类总圈复杂度)较高,原因是这三个类中承载了解析、计算和展开的工作,特别是SigmaFuncotry还涉及到对展开的式子单独进行Parse,任务较重。
UML类图
以下分别是前三次作业UML类图。
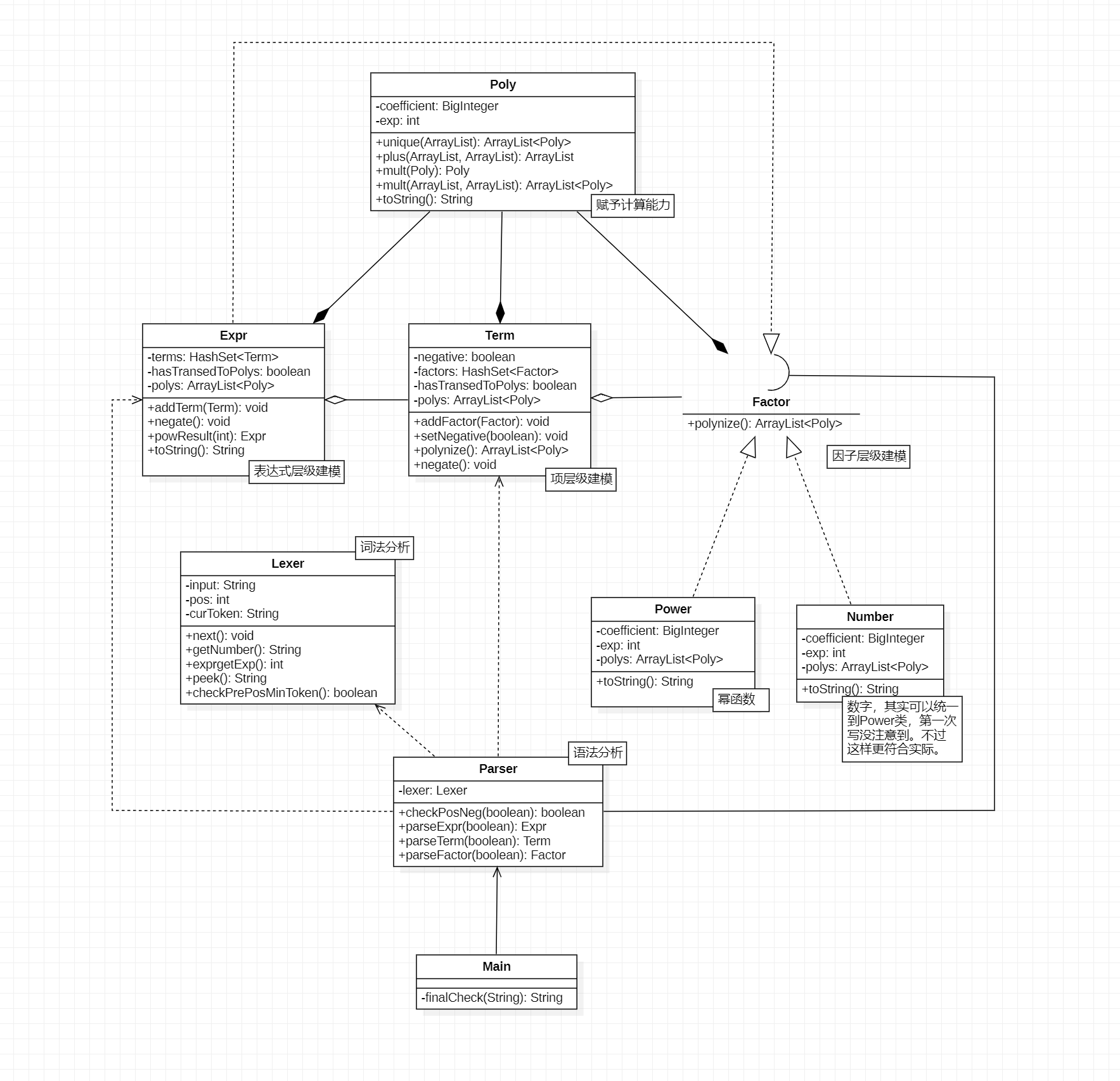
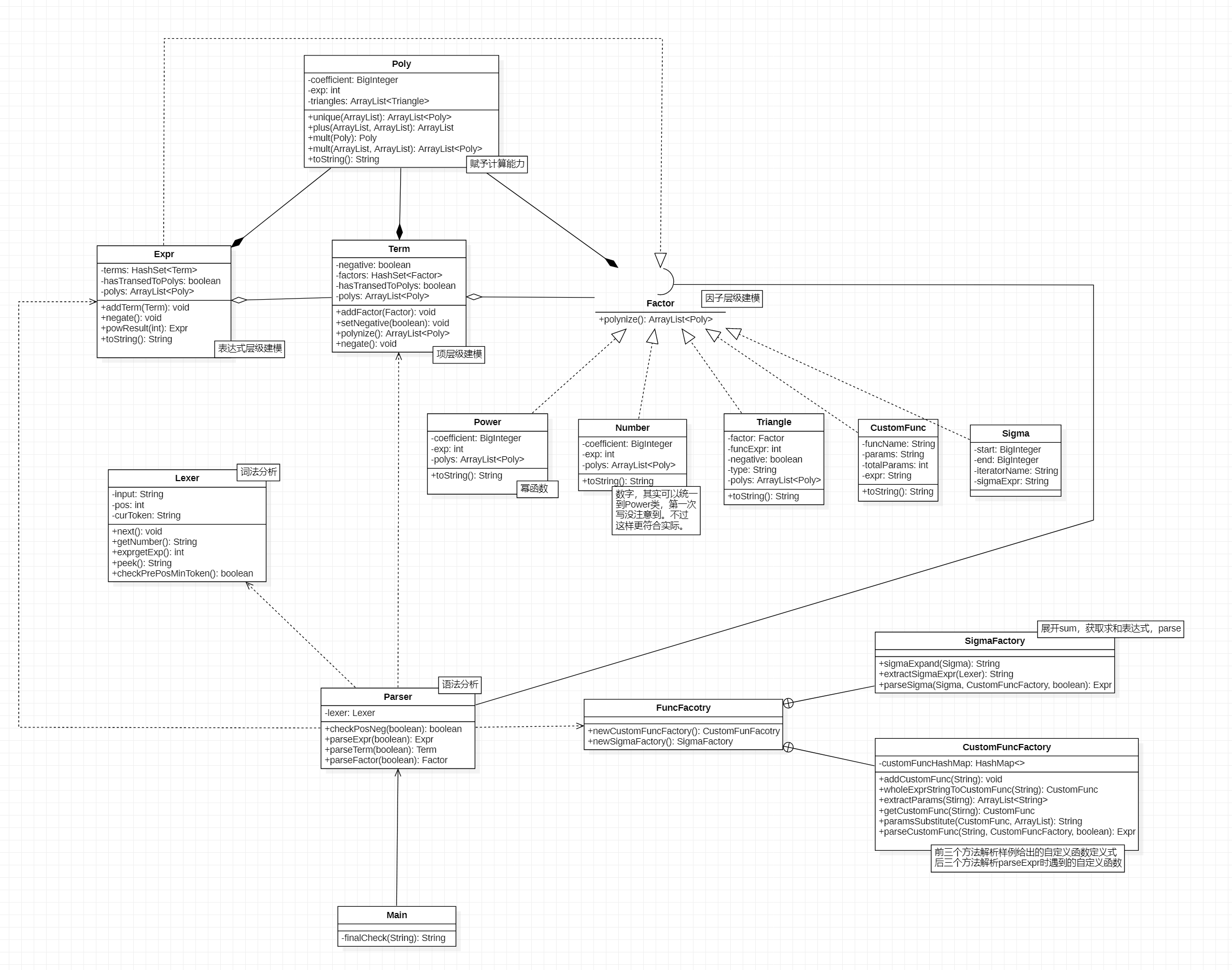
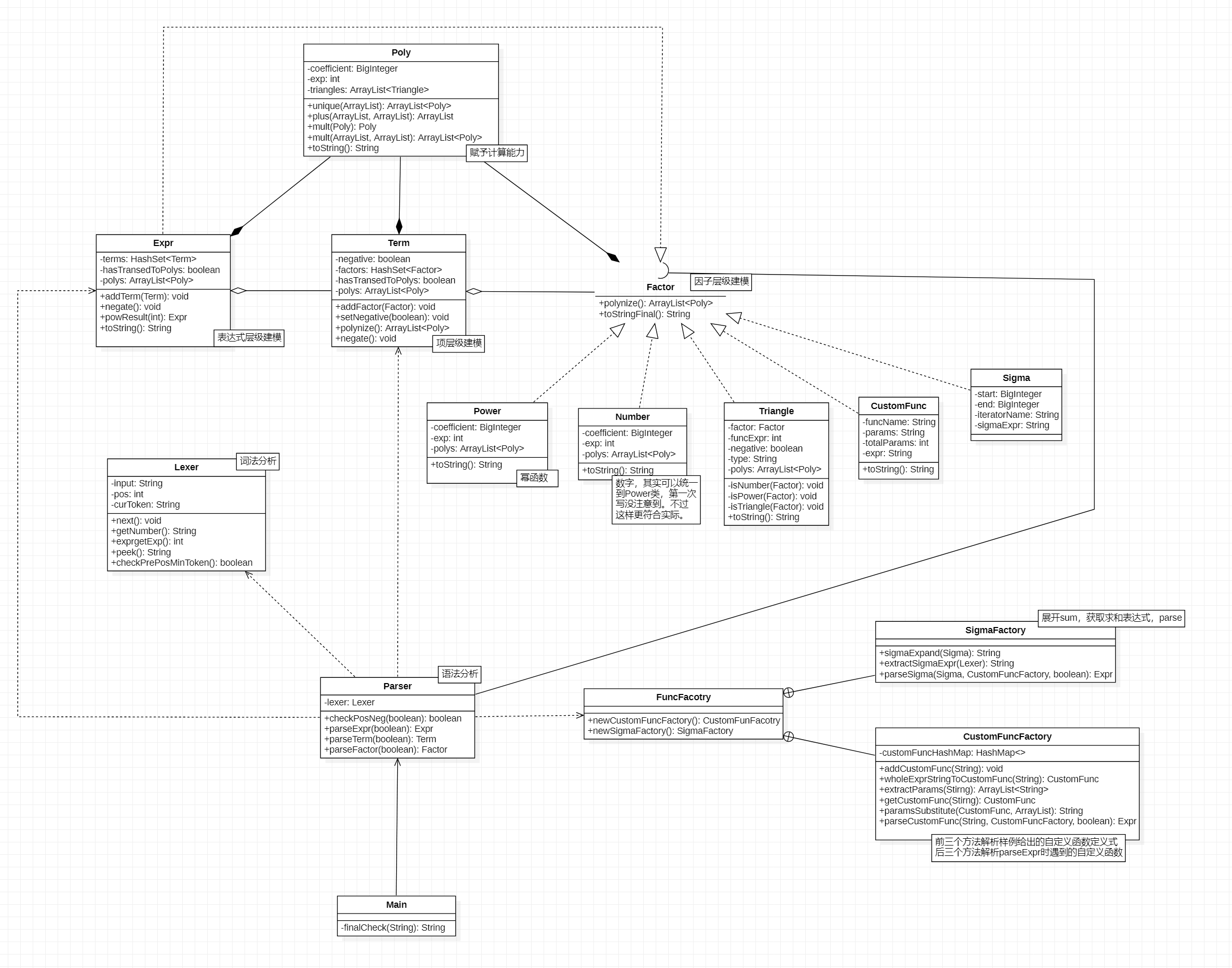
其中,对于每个类的解释以Text Box的形式附在了UML图中。在前三个小节也有对我认为比较重要的类或方法的说明,为节约版面不再复述。
优点:尽可能的根据数学语义解构表达式,直观,便于维护。
缺点:Factory承载了太多,导致圈复杂度略高,应该还可以继续拆解。
5 bug分析
hw1:交了一个半成品,强测爆零,很多功能在hw2中才得到了完善。
hw2:强测均过,互测未测出bug。
hw3:强测均过,互测测出两个bug,均为细节上的问题。侧面反映出细节决定成败方法要与需求同步迭代。
第三次作业sum中可以出现"i**2"的情况,直接代入数字无法解析,需要在数字两边加括号。
另一个bug是在isPower的判断中忘记-x也是表达式因子,程序出现sin(-x)的错误。
两个bug在4行内同时得到了修复。
6 hack策略
从个人经验来看,越小的数据越容易出问题。用常见的边界条件手造一些小数据效果还不错。
7 架构过渡
三次作业中架构保持了连续性,迭代开发很方便,没有经过重构。其中,第一个架构向第二个架构过渡中新增了Triangle、CustomFunc、Sigma因子,并在计算类Poly中新增了有关Triangle的处理。第二次向第三次过渡,只在Triangle类中加入了对因子的判断,及Factor中加入了输出前用到的toStringFinal方法。
第一次作业经历了一次不小的重构,直接导致时间不够,迫不得已交了个半成品上去,结果自然是G。后面看,重构不可避免,越早重构迭代越顺利。
提前为下次迭代留下接口,事半功倍。
8 心得体会
我们在上面向对象,到底什么是面向对象?没有人给我们准确的定义。只能自己体会。

