day19-Haddop
day19-Haddop
Haddop-HDFS
算法复杂度
- 算法复杂度分为时间复杂度和空间复杂度
- 时间复杂度是指执行这个算法所需要的计算工作量
- 空间复杂度是指执行这个算法所需要的内存空间
- 时间和空间都是计算机资源的重要体现,而算法的复杂性就是体现在运行该算法时的计算机所需的资源
空间复杂度
- 一个程序的空间复杂度是指运行完一个程序所需内存的大小
- 利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计
- 程序执行时所需存储空间包括以下两部分:
- 固定空间:主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间
- 可变空间:这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等
- 如何判断一个年份是平年还是闰年?
- 方法一:使用年份计算公式进行计算
- 方法二:创建一个长度4000的数组,以年份为下标,直接取值即可。
- 如果计算的年份超过1万年
时间复杂度
- 一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需要知道哪个算法花费的的时间多,哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句执行次数成正比,哪个算法中语句执行次数多,它花费的时间就多。
- 一个算法中的语句执行次数称为语句的频度或时间频度。记为:T(n)
T(n)=n^2+3n+4
T(n)=4n^2+2n+1
他们执行的频度是不同的,但是时间复杂度一样
- 为了描述时间频度变化引起的变化规律,引入时间复杂度的概念。记为O(n)
- 时间复杂度计算规则只需要遵循如下规则:
- 用常数1来取代运行时间中所有加法常数
- 只要高阶项,不要低级项
- 不要高阶项系数
- 时间频度不同,但时间复杂度可能相同
- T(n)=n^2+3n+4 -- n^2+3n -- n^2
- T(n)=4n^2+2n+1 -- 4n^2+2n -- 4n^2 -- n^2
- 他们的频度不同但时间复杂度相同,O(n^2)
- T(n)=log2n n+ 2n +10 -- log2n n+ 2n -- log2n*n -- logn^2
- 常见的时间复杂度场景
- O(1) -- 常数阶
- O(n) -- 线性阶
- O(logn) -- 对数阶
- O(n^2) -- 平方阶
- O(nlogn) -- 线性对数阶
- O(1)<O(logn)<O(n)<O(n2)<O(2n)<O(n!)<O(n^n)
- 时间复杂度去估算算法优的时候注重算法的潜力
- 有100条数据的时候算法a比算法b快
- 有10000条数据的时候算法b比a快
- 算法b的时间复杂度更优
时间与空间的取舍
- 日常操作中:我们都注重时间复杂度,有些特俗情况下,空间复杂度可能会更加重要
- 因为很多时候空间复杂度可以花钱解决
- 获取明天现在这个时刻?
- 请用代码获取明天这个时刻
- Thread().sleep(3600*24)
- Date() date=new Date();
- 以后时间复杂度的问题具体情况还要具体分析,两行代码执行一天
- 请用代码获取明天这个时刻
- 编程的精髓和美,并不在于一方的退让和妥协。而是在于两者之间取一个平衡点,完成华丽变身
- 但是将来工作中一切以时间复杂度为标准
十大排序算法
默认以升序排列(小--大)
冒泡
- 从位置0开始,当前位置数字与后面位置的数字进行比较
- 如果前面的数字大于后面的数字,数据交换
- 将位置向后移动一位,重复第一个过程,直到最后一个
- 重复刚才的过程
- 时间复杂度O(n^2)
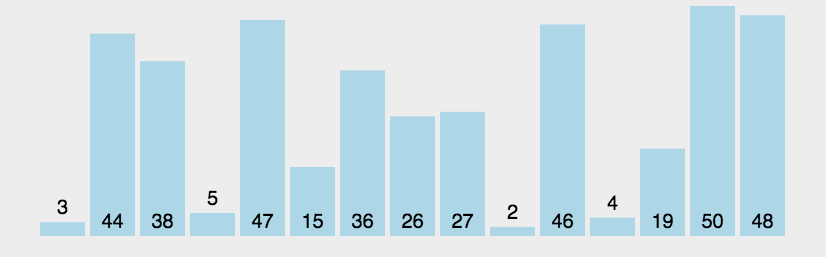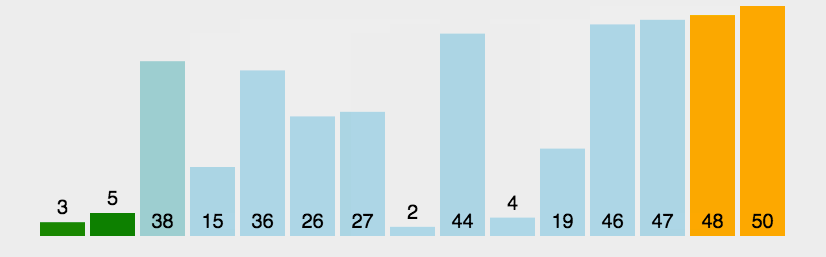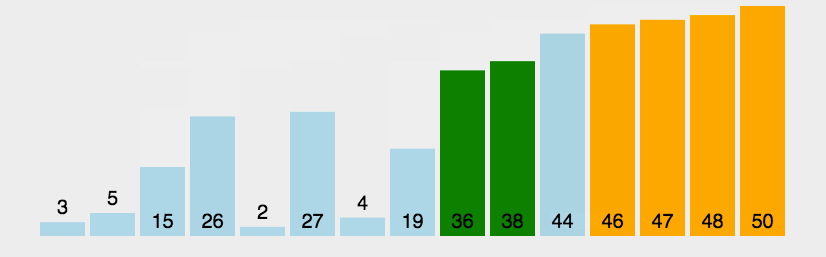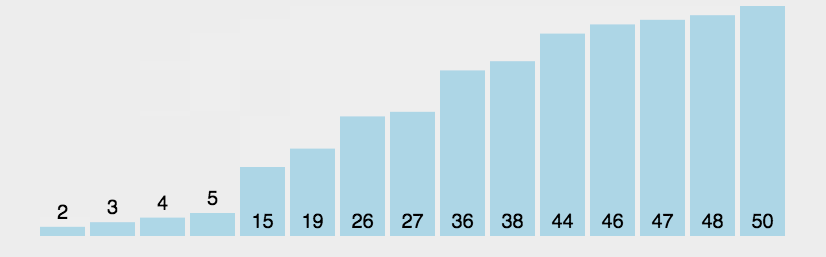
选择
- 假设第一个数字就是最大数字,记录他的索引
- 然后和后面的数字进行比较,如果后面的数字大于最大数字,重新记录新数字的索引
- 直到最后一个数字,然后将最大数字索引与最后一个数字进行交换
- 时间复杂度O(n^2)
插入
- 假设原始数据是有序的
- 每次向数列中插入一个数字,从右向左依次比较,找到合适的位置
- 数列重新变为有序数列
- 在向数列中插入一个数字
- 时间复杂度O(n^2)
希尔
- 红豆 绿豆 黄豆 黑豆 酱豆 混合一堆
- 方案1:手动捡出来
- 方案2:筛子 -- 红豆,绿豆 -- 然后手捡出来
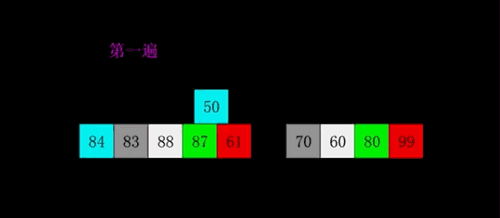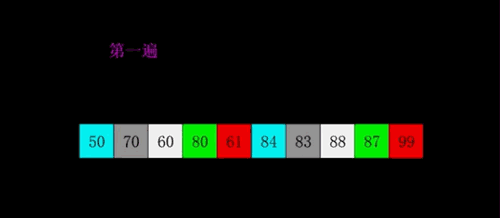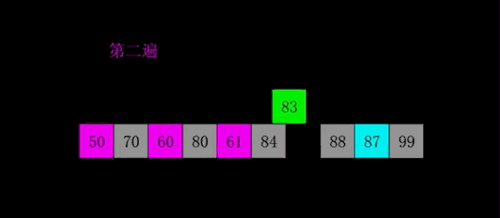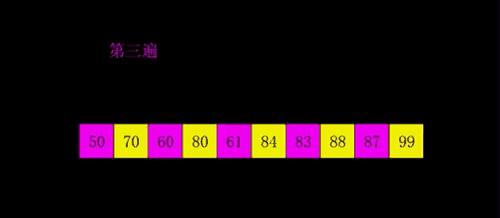
- 将数组递归分组,首先分为长度/2组
- 然后将第一个数字与1+组进行插入排序,经过第一次在整体排序后,小的数字很快会被移动到前面
- 重新将数组分组,原来组/2
- 小的数字很快就会被移动到前面
- 时间复杂度O(n^1.3)
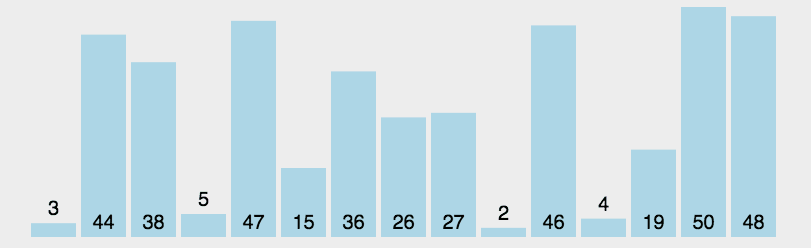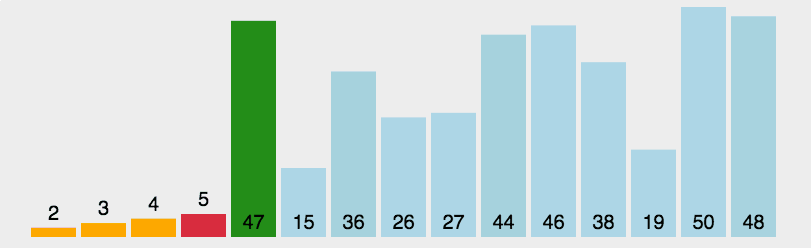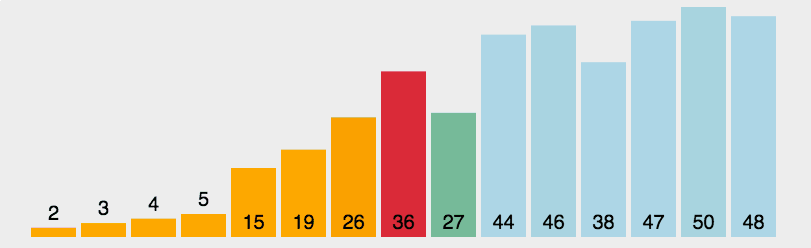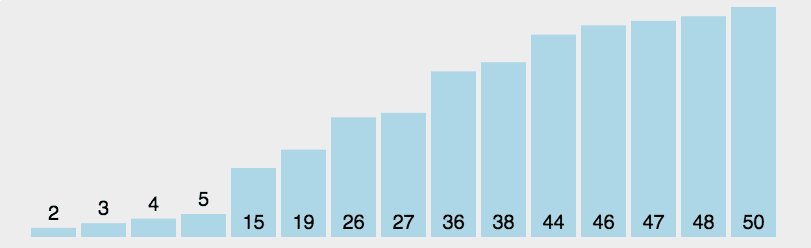
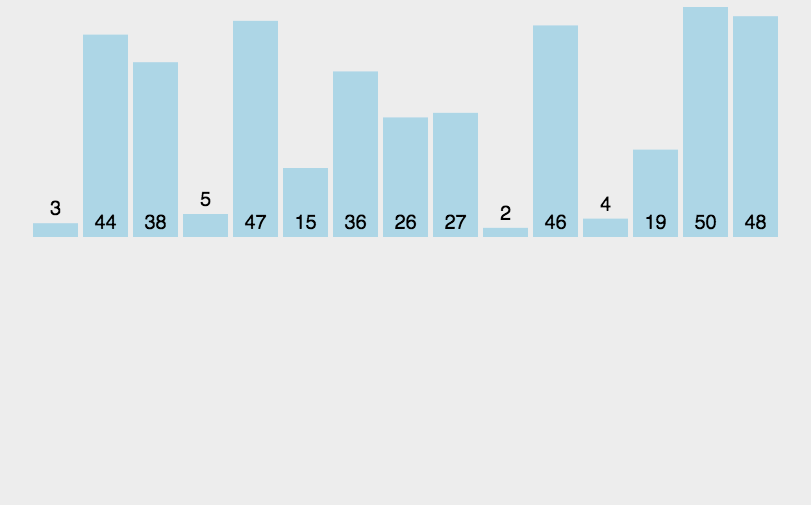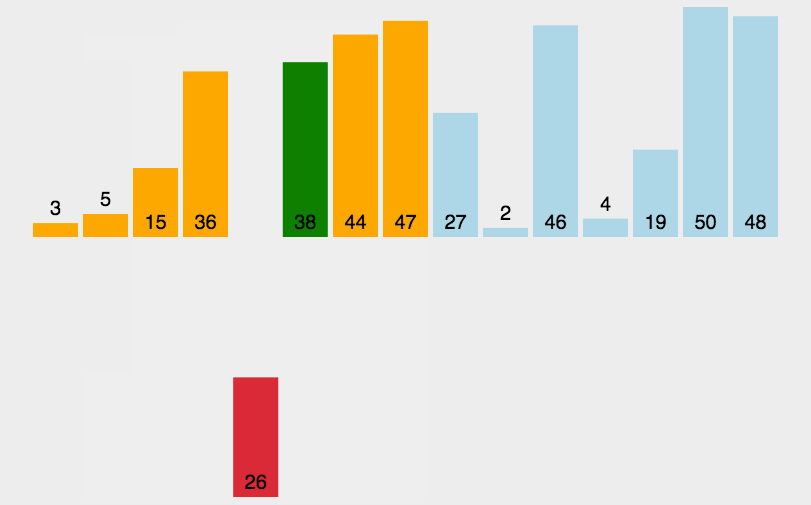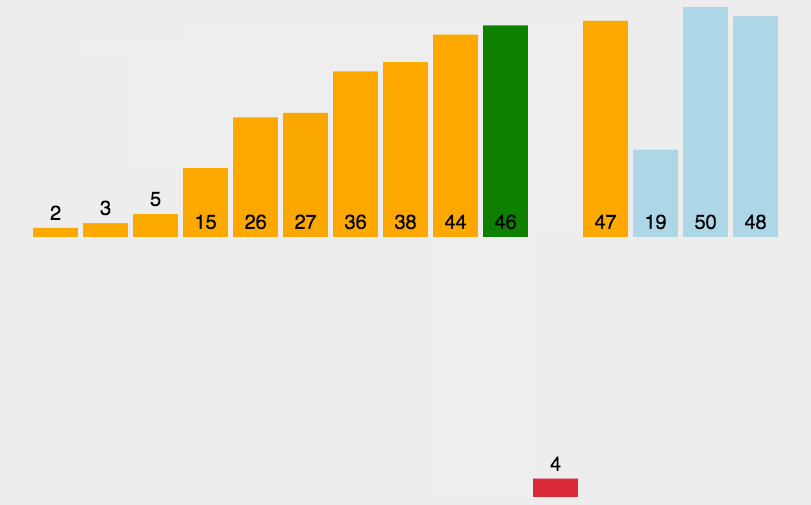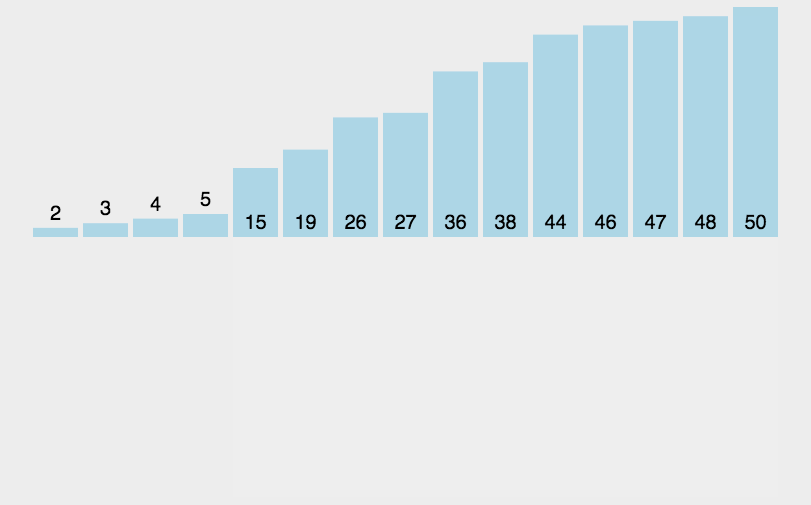
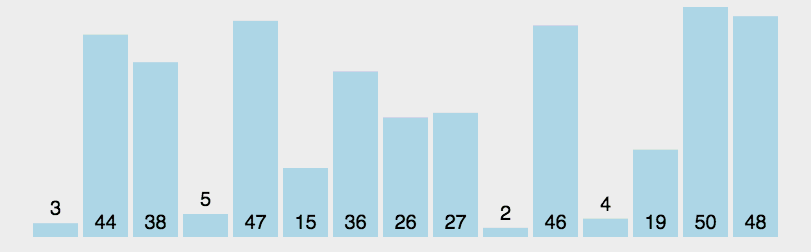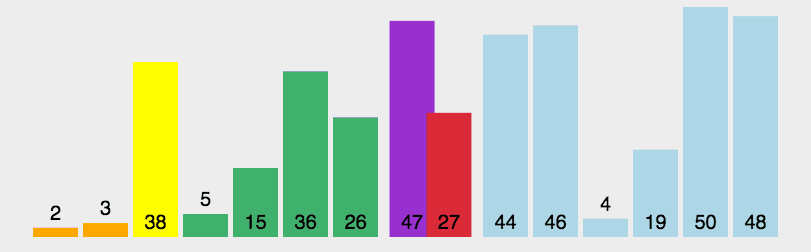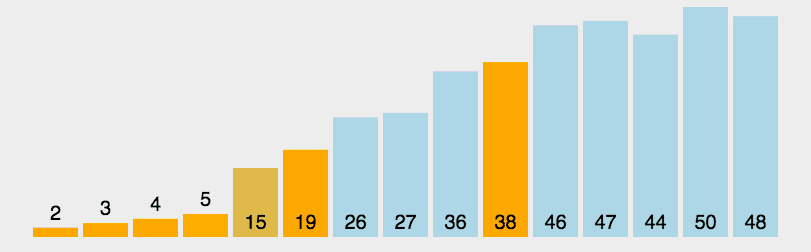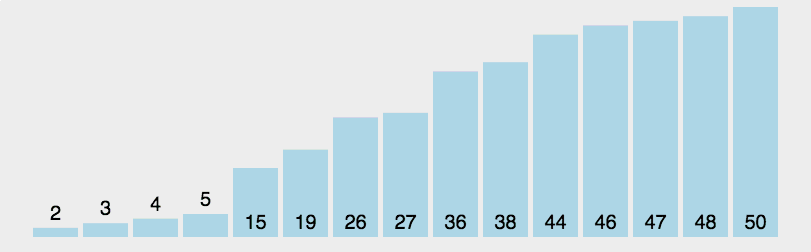
快速
- 三种(挖坑法 左右法 前后法)
- 操作:选择一个数字作为参照物(基准数字)5
- 思想:然后和另外一个的进行比较,如果是右边的小于5就交换,5左边的大于5就交换
- 整体排序之后,5的位置是正确的,左右两个是无序
- 将左右两个都当作一个新序列进行排序基准数
- 时间复杂度O(nlog2n)
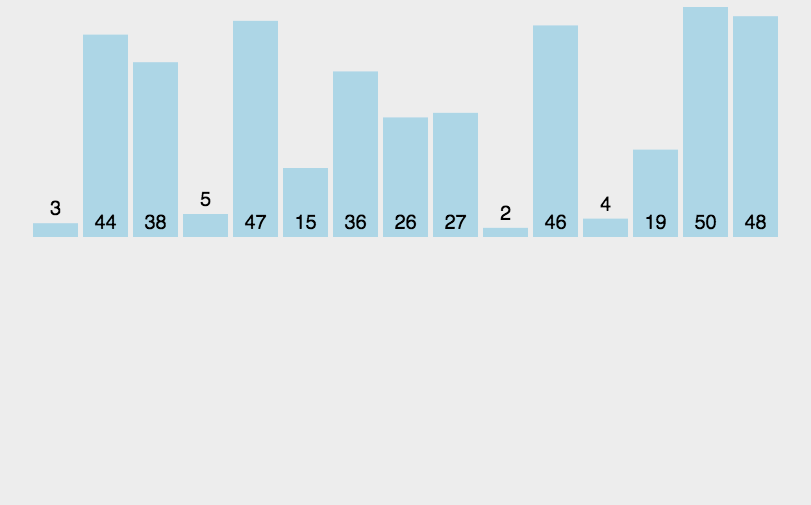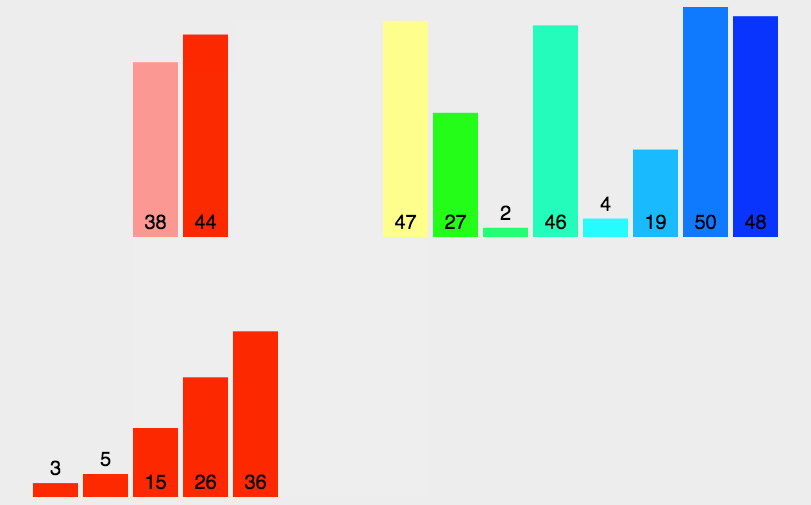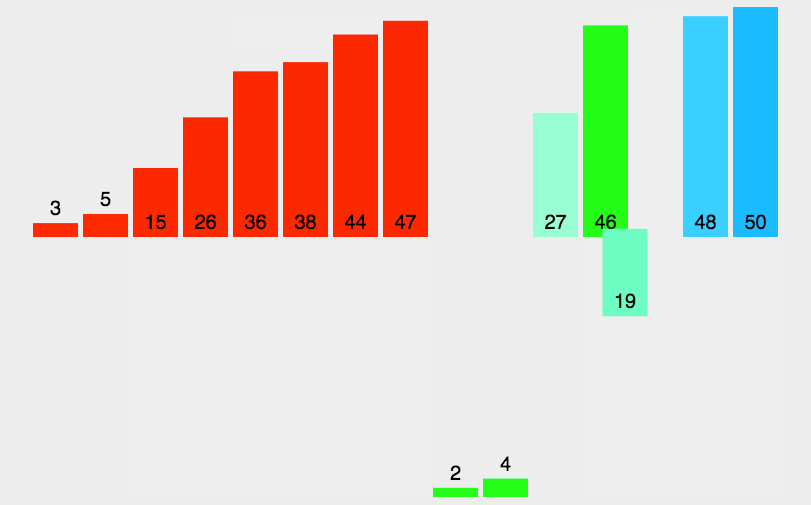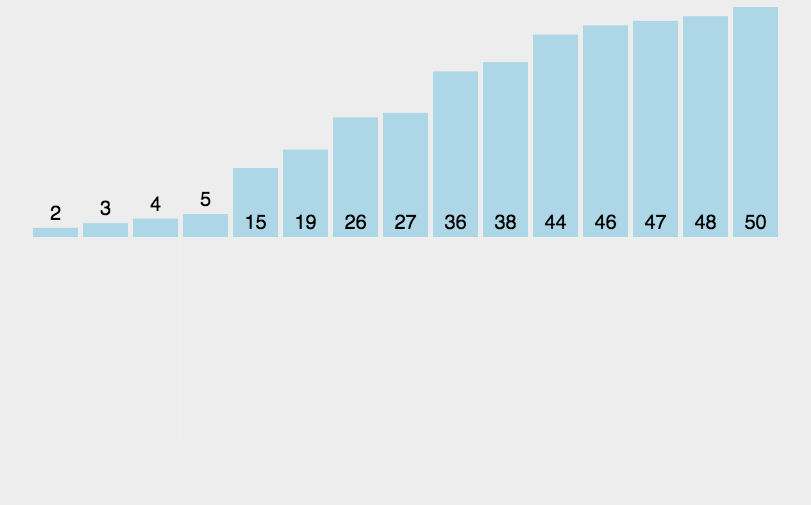
归并
- 让两个有序对列进行比较,然后每个队列依次取出1个数字比较,然后小的数字被去除
- 分割
- 依次将数列分割二等分,二等分之后的子序列继续二等分
- 直到每个子序列只有一个数字,停止分割
- 合并
堆
- 一种基于树的排序算法
- 二分查找树
- 任意节点
- 最多有两个节点
- 左面的节点都小于父节点
- 右边的节点都大于父节点

计数
- 一种很巧妙的排序算法
- 比较特殊的排序算法,只针对特殊数据的排序
- 将对应的数据让数组的索引值+1
- 最后遍历数组,索引对应的值是几就打印几
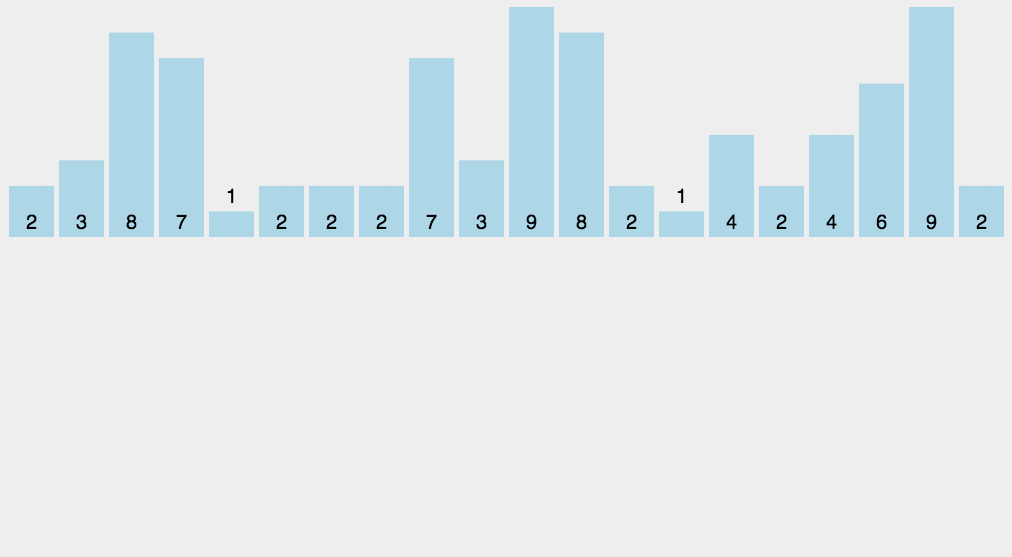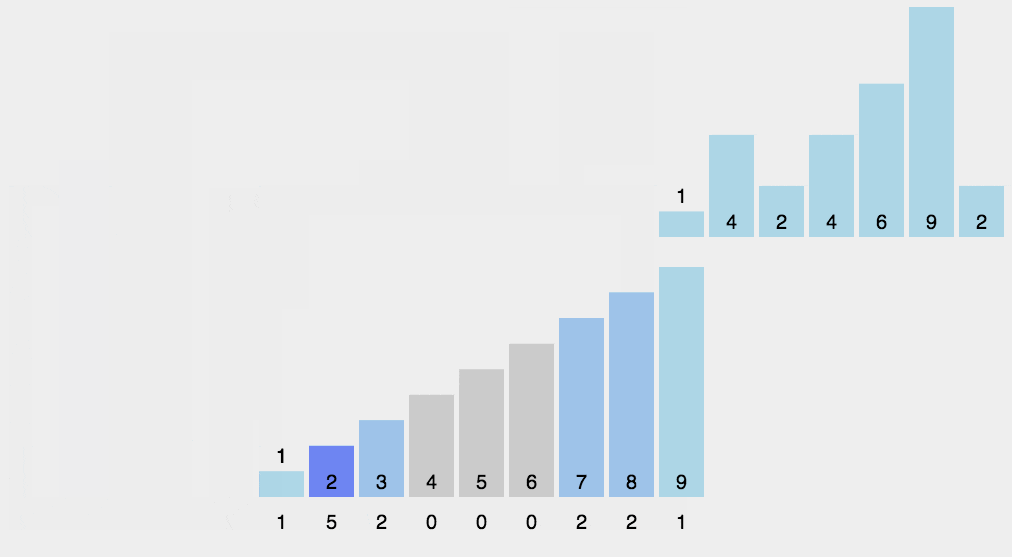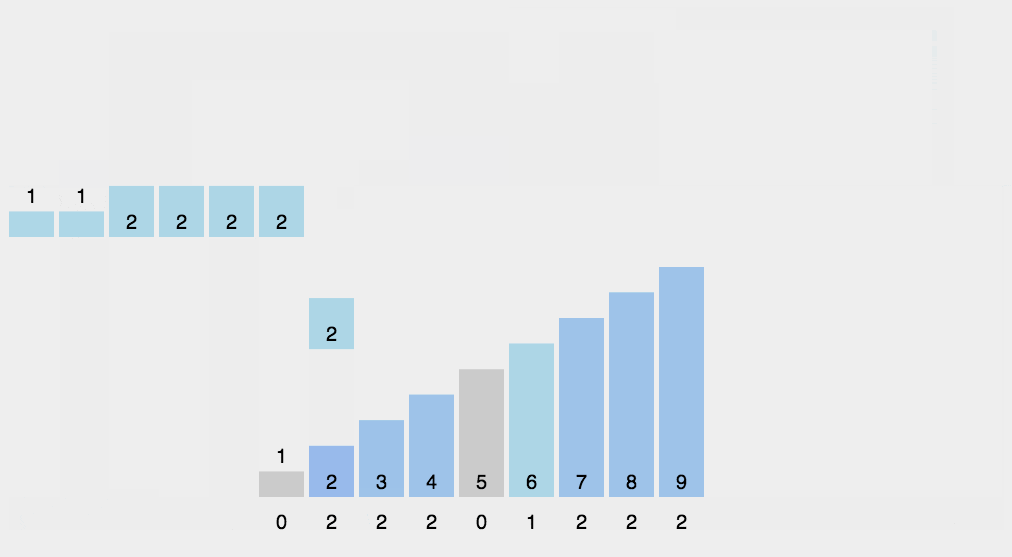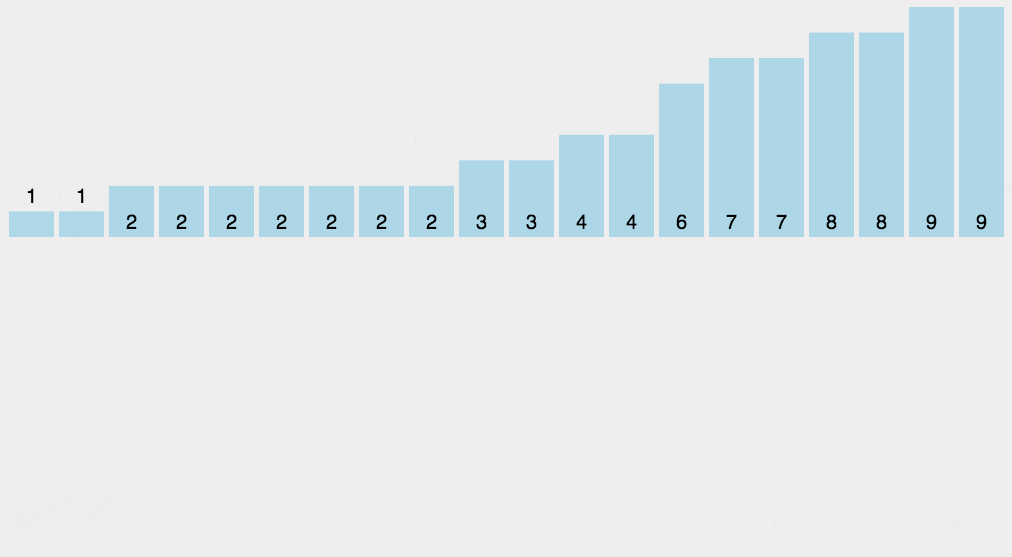
桶
- 将数字按照范围进行分割
- 然后对分割后的数据进行排序(继续分割)
- 将来数据分桶要特别注意数据倾斜的问题
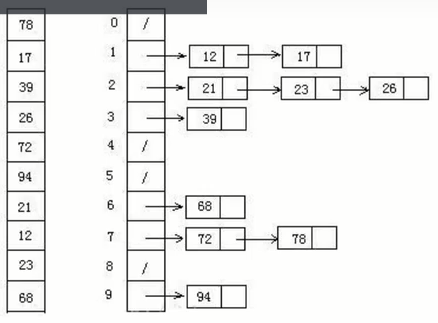
基数
- 基数排序是按照地位先排序,然后收集,再按照高位排序,然后再收集,依次类推,直到到最高位




 浙公网安备 33010602011771号
浙公网安备 33010602011771号