浅谈高斯消元
一.简介
高斯消元法,我们在线性代数里面的是学过的,它的主要用途是求解n元一次线性方程组。
举个例子,下面这个就是一个4元一次方程组
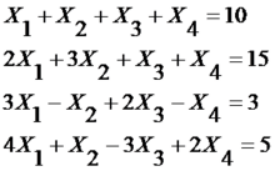
我们可以把它化成一个大小为4*5的矩阵

在求解之前,我们首先要了解一下几个线性方程组的基本性质
- 矩阵中任意两行交换位置,解不变。
- 同一行乘上同一个数,解不变。
- 同一行乘上同一个数再加上另一个方程,解不变
接下来,我们来讲解下具体过程,我们的目的就是完成消元后,对于左边的系数矩阵,每一行都有且只有一个数不为0。具体方法就是用上面的运用上面的原理。具体步骤如下
- 枚举每一行,一行一行的处理;
- 我们规定第i行存的是xi的解,因为精度问题,我们首先要找出i+1到n里xi最大系数的那一行交换到当前第i行。
- 接下来,我们要去消除其他行里的xi,具体做法就是将当前行的xi的系数乘上xj/xi,然后用第j行减去第i行。
- 枚举结束后直接输出结果即可。
二.代码实现
#define re register #define maxn 105 #define D double D a[maxn][maxn]; for(re int i = 1; i<=n; ++i) { for(re int j = 1; j<=n+1; ++j) scanf("%lf",&a[i][j]); } for(re int i = 1; i<=n; ++i) { re int max = i; for(re int j =i+1; j<=n; ++j) { if(fabs(a[j][i])>fabs(a[max][i])) max =j; } for(re int j =1 ; j<=n+1; ++j) swap(a[i][j],a[max][j]); if(!a[i][i])//如果有一项最大值都为0,则无解 { puts("No Solution"); return 0; } for(re int j =1; j<=n+1; ++j) { if(j!=i) { re D temp =a[j][i]/a[i][i]; for(re int k = i+1; k<=n+1; ++k) { a[j][k]-=temp*a[i][k]; } } } } for(re int i =1; i<=n; ++i) printf("%.2lf\n",a[i][n+1]/a[i][i]);
三.相关习题
过往不恋 未来不迎 当下不负


 浙公网安备 33010602011771号
浙公网安备 33010602011771号