202505 SD 二轮省集总结
题目和知识点的具体内容等我回去悟一悟再写吧。。。。。。
Day0
打热身赛。分数:\(0+0+0=0\)
T1 是某年某地 icpc 的原。T2、T3 都不会,后来也没订。
看 T1 一会之后感觉是树上选一些路径覆盖整棵树,然后想到可以是容斥,但是觉得这题正解肯定不是容斥,所以没写,想了半天别的解法,然后写了 T2 二十分暴力走了。后来发现正解就是容斥,当时其实已经想到对的状态设计了,甚至感觉前几天写过比较类似的。Day1 晚上把这题订了。
T1
给定一张无向连通图,无重边自环。求有多少种合法的加边方案,可以使加入这些边后,整张图无重边、自环,且边双连通。(\(n\le 5000\))
对原图边双缩点后得到一棵树,发现在树上两点间连边相当于在树上选择了一条路径,这条路径上所有的点都在一个边双里,然后问题就转化为树上有多少种选择路径的方式使得任意一个点都至少被一条路径包含。
考虑容斥,设 \(f_{i,j}\) 表示节点 \(i\) 的子树中,\(i\) 所在连通块大小为 \(j\) 所有可能的路径方案数。状态转移
第一个公式中 \(2^{jk-1}\) 是两边双间的连边方案数,减去 1 是因为其中恰好一条边在原图上。但是复杂度好像是 \(O(n^3)\),不过其实转移时只枚举到上界也就是子树大小,可以证明复杂度是 \(O(n^2)\) 的。最后答案是 \(\sum f_{1,i}\Pi 2^{cnt_j}\),其中 \(cnt_{j}\) 表示边双 \(j\) 中不在原图上的边数。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read()
{
int t=0;char h=getchar();
while(!isdigit(h))h=getchar();
while(isdigit(h))t=(t<<1)+(t<<3)+(h^48),h=getchar();
return t;
}
void write(int x)
{
if(x>9)write(x/10);putchar(x%10+'0');
}
const int mod=998244353;
const int N=5010;
const int M=1e6+10;
int dfn[N],low[N],now=0;
bool e[M*2];
ll p[N*N/2],g[N],f[N][N];
int num[N],siz[N];
int en[N];
int col[N],cnt=0;
ll ans=0,z=mod-1;
struct graph{
int lk[N],nxt[M*2],to[M*2],len=1;
inline void insert(int x,int y)
{
to[++len]=y;nxt[len]=lk[x];lk[x]=len;
}
void tarjan(int x,int las=0)
{
dfn[x]=low[x]=++now;
for(int i=lk[x];i;i=nxt[i])
{
int y=to[i];
if(!dfn[y])
{
tarjan(y,i^1);low[x]=min(low[x],low[y]);
if(low[y]>dfn[x])e[i]=e[i^1]=true;
}
else if(i!=las)low[x]=min(low[x],dfn[y]);
}
}
void dfs(int x)
{
col[x]=cnt;++num[cnt];
for(int i=lk[x],y;i;i=nxt[i])if(!col[y=to[i]]&&!e[i])dfs(y);
}
void dfs2(int x,int fa=0)
{
siz[x]=num[x];
f[x][num[x]]=1;
for(int i=lk[x],y;i;i=nxt[i])
{
if((y=to[i])==fa)continue;
dfs2(y,x);
for(int i=1;i<=siz[x]+siz[y]+1;i++)g[i]=0;
for(int i=0;i<=siz[x];i++)
for(int j=0;j<=siz[y];j++)
(g[i+j]+=f[x][i]*f[y][j]%mod*((p[i*j-1])%mod)%mod)%=mod,
(g[i]+=f[x][i]*z%mod*f[y][j]%mod)%=mod;
if(g[siz[x]+siz[y]+1])siz[x]+=siz[y]+1;
else siz[x]+=siz[y];
for(int i=0;i<=siz[x];i++)f[x][i]=g[i];
}
// if(siz[x]==1)f[x][1]=1;
}
}g1,g2;
int n,m;
int x,y;
int main()
{
// freopen("ex_a2.in","r",stdin);
n=read();m=read();p[0]=1;
for(int i=1;i<=n*n/2;i++)p[i]=(p[i-1]<<1)%mod;
for(int i=1;i<=m;i++)x=read(),y=read(),g1.insert(x,y),g1.insert(y,x);
g1.tarjan(1);
for(int i=1;i<=n;i++)if(!col[i])++cnt,g1.dfs(i);
for(int i=2;i<=g1.len;i+=2)
if((x=col[g1.to[i]])!=(y=col[g1.to[i^1]]))g2.insert(x,y),g2.insert(y,x);
else ++en[x];
g2.dfs2(1);
// for(int i=1;i<=n;i++)cout<<f[i][0]<<" "<<f[i][1]<<" "<<f[i][2]<<" "<<f[i][3]<<"\n";puts("");
for(int i=0;i<=n;i++)(ans+=f[1][i])%=mod;
for(int i=1;i<=cnt;i++)(ans*=p[num[i]*(num[i]-1)/2-en[i]])%=mod;// 相当于 cnt[i]
write(ans);
return 0;
}
Day1
tsx 出题 + 讲课。分数:\(50+16+0=66\)
上午模拟赛,T1 写了 50pts,一开始特别困,非常困,非常困,非常困,想也想不出来,感觉没有进行任何有效的思考,然后 30 分 \(n^3\) + 20 分性质。T2 16 分 \(n^3\)。T3 爆搜 0 分。
听完讲题感觉 T1 性质想得不够多,我当时太困了,而且一直想不出来非常有用的就想摆。刚刚发现后边两题题解都没看。
讲课的时候讲了一些有意思的树上题目,但是我一道都没写。跟着想了几道题发现又是之前见过的思路但是我想不到。
晚上订了一下前一天的那个容斥。代码写出来努力调了一下调不对然后就去翻别人提交记录,发现写得挺像的只有个别地方不一样吧,,改了一下就过了。
T1 花卉港湾
给定一棵树,建新图与原图点集相同,原图上距离 \(\ge k\) 的所有点对在新图上建边,每次询问给出两点,求两点在新图上的最短距离,或者输出 \(-1\) 表示不能到达。
\(n^3\) 显然直接建图跑 Floyd,链的情况简单分讨一下。
通过对链的情况的分讨发现答案其实只有 \(-1,1,2,3\) 四种情况。\(1\) 的情况只需要判断两点距离是否 \(\ge k\) 。然后,树的直径有一个性质,对于树上一点,到该点距离最远的点一定是直径端点。(但是我当时不知道然后证了半天)那么如果一个点不能到达任何一个直径端点,答案就是 \(-1\)。
那么重点在于判断 \(2,3\) 的情况。如果存在一点 \(k\) 使得新图上存在 \(x\rightarrow k\rightarrow y\) 显然答案就是 \(2\),否则为 \(3\)。设将随便一条直径 \(p_1,p_2,...,p_m\) 上所有边删掉,原图变成一个森林,令每棵树上在原直径中的点为树 \(i\) 的根,设每个点 \(s\) 在新图上在 \(p_{r_s}\) 为根的树上,\(h_i\) 表示树\(i\) 的高,\(d_s\) 表示 \(s\) 在新树上的深度。然后问题转化为求是否有 \(k\not =r_x,r_y\),使得 \(|k-r_x|+h_k+d_x\ge k\),且\(|k-r_y|+h_k+d_y\ge k\)。把绝对值拆开分讨一下,然后想办法维护一下需要维护的信息。
点击查看代码
#include<bits/stdc++.h>
#define mid ((lf+rt)>>1)
#define swap(x,y) (x^=y^=x^=y)
#define pii pair<int,int>
#define f first
#define s second
using namespace std;
inline int read()
{
int t=0;char h=getchar();
while(!isdigit(h))h=getchar();
while(isdigit(h))t=(t<<1)+(t<<3)+(h^48),h=getchar();
return t;
}
void write(int x)
{
if(x<0)putchar('-'),x=-x;if(x>9)write(x/10);putchar(x%10+'0');
}
const int N=1e5+10;
int lk[N],to[N*2],nxt[N*2],len=1;
inline void insert(int x,int y)
{
to[++len]=y;nxt[len]=lk[x];lk[x]=len;
}
int dep[N],s;
int f[N][50];
void dfs(int x,int fa=0)
{
if(dep[x]>dep[s])s=x;
for(int i=lk[x],y;i;i=nxt[i])
{
if((y=to[i])==fa)continue;
dep[y]=dep[x]+1;dfs(y,x);f[y][0]=x;
}
}
int lmt=32;
inline int lca(int x,int y)
{
if(x==y)return x;
if(dep[x]<dep[y])swap(x,y);
for(int i=lmt;i>=0;i--)if(dep[f[x][i]]>=dep[y])x=f[x][i];
// cout<<"x: "<<x<<endl;
if(x==y)return x;
for(int i=lmt;i>=0;i--)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
return f[x][0];
}
inline int dis(int x,int y)
{
// cout<<x<<" "<<y<<" =w=. "<<lca(x,y)<<endl;
return dep[x]+dep[y]-2*dep[lca(x,y)];
}
int n,q,k;
bool vis[N];
int p[N],r[N],h[N],d[N],cnt=0;
void dfs1(int x,int rt)
{
r[x]=rt;vis[x]=true;if(d[x]>h[rt])h[rt]=d[x];
for(int i=lk[x],y;i;i=nxt[i])
{
if(vis[y=to[i]])continue;
d[y]=d[x]+1;dfs1(y,rt);
}
}
struct node{
vector<pii>v;
}t1,t2,z;
inline node operator+(node a,node b)
{
node c=a;c.v.insert(c.v.end(),b.v.begin(),b.v.end());
sort(c.v.begin(),c.v.end(),greater<pii>());
if(c.v.size()>3)c.v.resize(3);return c;
}
node num[N*8];
inline void upd(int x,node k,int p,int lf,int rt)
{
num[p]=num[p]+k;
if(lf==rt)return;
if(x<=mid)upd(x,k,p<<1,lf,mid);
else upd(x,k,p<<1|1,mid+1,rt);
}
inline node que(int l,int r,int p,int lf,int rt)
{
if(l<=lf&&rt<=r)return num[p];
if(r<=mid)return que(l,r,p<<1,lf,mid);
if(l>mid)return que(l,r,p<<1|1,mid+1,rt);
return que(l,r,p<<1,lf,mid)+que(l,r,p<<1|1,mid+1,rt);
}
inline int solve(int x,int y)
{
// cout<<x<<" "<<y<<" "<<dis(x,y)<<endl;
if(dis(x,y)>=k)return 1;
for(pii s:t1.v)if(s.f+r[x]+d[x]>=k&&s.f+r[y]+d[y]>=k)return 2;
for(pii s:t2.v)if(s.f-r[x]+d[x]>=k&&s.f-r[y]+d[y]>=k)return 2;
node t=que(max(1,k+r[x]-d[x]),n<<1,1,1,n<<1);
for(pii s:t.v)if(s.f+r[y]+d[y]>=k)return 2;
if(dis(x,p[1])>=k&&dis(y,p[cnt])>=k||dis(x,p[cnt])>=k&&dis(y,p[1])>=k)return 3;
return -1;
}
int x,y;
int main()
{
// freopen("b.in","r",stdin);
n=read();q=read();k=read();
for(int i=1;i<n;i++)x=read(),y=read(),insert(x,y),insert(y,x);
dfs(1);dep[s]=0;for(int i=1;i<=n;i++)f[i][0]=0;
dfs(s);lmt=log2(n)+1;
for(int j=1;j<=lmt;j++)
for(int i=1;i<=n;i++)f[i][j]=f[f[i][j-1]][j-1];
for(int i=s;i;i=f[i][0])p[++cnt]=i,vis[i]=true;
for(int i=1;i<=cnt;i++)
{
d[p[i]]=0;dfs1(p[i],i);
node a=z;a.v.push_back({h[i]-i,i});t1=t1+a;
node b=z;b.v.push_back({h[i]+i,i});t2=t2+b;
upd(h[i]+i,a,1,1,n<<1);
}
while(q--)
{
x=read();y=read();if(r[x]>r[y])swap(x,y);write(solve(x,y));puts("");
}
return 0;
}
T2 礎石花冠
给出两个序列 \(a,b\),对于 \(i,j\) ,满足 \(i<j\),如果 \(a_i<b_j\) 则存在 \(i\rightarrow j\),否则存在 \(j\rightarrow i\)。再给出 \(m\) 对点,删除图上这两点的连边。设按照以上方法得到的图为图 \(G\),求出一个边数最少的 \(f(G)\),使得 \(G\) 与 \(f(G)\) 的传递闭包相同。
\(O(n^3)\) 做法,首先暴力建图求出强连通分量并缩点,得到新的 DAG,对于每条边 \((x,y)\) 枚举所有点,如果存在点 \(z\) 使得存在路径 \(x\rightarrow z\rightarrow y\),\((x,y)\) 这条边就是没有必要存在的。SCC 内部显然连成一个环比较优秀。
考虑用 Kosaraju 算法求SCC。用线段树维护未被访问节点 \(a,b\) 的最小/大值,对于每次寻找出边 \(O(\log n)\) 查询。总复杂度 \(O((n+m)\log n)\)。
对于得到的 DAG 求 \(f(G)\),考虑对于拓扑序倒序进行。对于已有 \([i+1,n]\) 节点的图,考虑加进去节点 \(i\) 的过程。复制一张已有的图,对于上面每个零入度的点,如果存在边 \(i\rightarrow x\) 就在图上连边,否则删掉 \(x\) 及其所有出边,继续寻找零入度点并重复上述过程。考虑优化,发现并不需要真的把整张图复制下来,只需要维护点的入度。可以证明时间复杂度为 \(O((n+m)\sqrt m)\)。
点击查看代码
#include<bits/stdc++.h>
#define pii pair<int,int>
#define mid ((lf+rt)>>1)
#define vi vector<int>
#define inf 0x3f3f3f3f
#define pb push_back
#define s second
#define f first
using namespace std;
inline int read()
{
int t=0;char h=getchar();
while(!isdigit(h))h=getchar();
while(isdigit(h))t=(t<<1)+(t<<3)+(h^48),h=getchar();
return t;
}
void write(int x)
{
if(x>9)write(x/10);putchar(x%10+'0');
}
const int N=1e5+10;
int n,m;
pii ax[N*4],bx[N*4],an[N*4],bn[N*4];
inline void psu(int p)
{
ax[p]=max(ax[p<<1],ax[p<<1|1]);bx[p]=max(bx[p<<1],bx[p<<1|1]);
an[p]=min(an[p<<1],an[p<<1|1]);bn[p]=min(bn[p<<1],bn[p<<1|1]);
}
int a[N],b[N];
void build(int p,int lf,int rt)
{
if(lf==rt)
{
ax[p]=an[p]={a[lf],lf};bx[p]=bn[p]={b[lf],lf};return;
}
build(p<<1,lf,mid);
build(p<<1|1,mid+1,rt);
psu(p);
}
void del(int x,int p,int lf,int rt)
{
if(lf==rt)
{
ax[p]=bx[p]={-inf,0};an[p]=bn[p]={inf,0};return;
}
if(x<=mid)del(x,p<<1,lf,mid);
else del(x,p<<1|1,mid+1,rt);
psu(p);
}
pii quex(int l,int r,int p,int lf,int rt,pii*mx)
{
if(l<=lf&&rt<=r)return mx[p];
if(l>mid)return quex(l,r,p<<1|1,mid+1,rt,mx);
if(r<=mid)return quex(l,r,p<<1,lf,mid,mx);
return max(quex(l,r,p<<1,lf,mid,mx),quex(l,r,p<<1|1,mid+1,rt,mx));
}
pii quen(int l,int r,int p,int lf,int rt,pii*mn)
{
if(l<=lf&&rt<=r)return mn[p];
if(l>mid)return quen(l,r,p<<1|1,mid+1,rt,mn);
if(r<=mid)return quen(l,r,p<<1,lf,mid,mn);
return min(quen(l,r,p<<1,lf,mid,mn),quen(l,r,p<<1|1,mid+1,rt,mn));
}
vector<pii>s[N];
bool vis[N];
int st[N],top=0;
void dfs1(int x)
{
// cout<<x<<"ddd"<<endl;if(x==3)cout<<s[x].size()<<"=w=.\n";
del(x,1,1,n);vis[x]=true;
for(pii t:s[x])
{
int l=t.f,r=t.s;
while(x<l)
{
pii t2=quex(l,r,1,1,n,bx);
if(a[x]<t2.f)dfs1(t2.s);else break;
}
while(x>r)
{
pii t2=quex(l,r,1,1,n,ax);
if(b[x]<t2.f)dfs1(t2.s);else break;
}
}
st[++top]=x;
}
int col[N],cnt,sum[N];
vi v[N];
void dfs2(int x)
{
del(x,1,1,n);vis[x]=false;col[x]=cnt;v[cnt].pb(x);
for(pii t:s[x])
{
int l=t.f,r=t.s;
while(x<l)
{
pii t2=quen(l,r,1,1,n,bn);
if(a[x]>t2.f)dfs2(t2.s);else break;
}
while(x>r)
{
pii t2=quen(l,r,1,1,n,an);
if(b[x]>t2.f)dfs2(t2.s);else break;
}
}
}
map<pii,int>num;
inline bool edge(int x,int y)
{
if(x>y)swap(x,y);return num[{x,y}]<1ll*v[x].size()*v[y].size();
}
int lk[N],nxt[N*4],to[N*4],len=0;
inline void insert(int x,int y)
{
to[++len]=y;nxt[len]=lk[x];lk[x]=len;
}
inline void add(int x,int y)
{
write(x),putchar(' '),write(y),puts("");
}
int ind[N],cur[N];
int x[N],y[N];
vi e[N],g,h;
int ans=0;
int main()
{
// freopen("b.in","r",stdin);
n=read();m=read();
for(int i=1;i<=n;i++)a[i]=read(),e[i].pb(i),e[i].pb(n+1);
for(int i=1;i<=n;i++)b[i]=read();
for(int i=1;i<=m;i++)
{
x[i]=read();y[i]=read();
e[x[i]].pb(y[i]);e[y[i]].pb(x[i]);
}
for(int i=1;i<=n;i++)
{
sort(e[i].begin(),e[i].end());
int las=0;
for(int x:e[i])
{
if(las+1<x)s[i].pb({las+1,x-1});las=x;
}
}
build(1,1,n);
for(int i=1;i<=n;i++)if(!vis[i])dfs1(i);
build(1,1,n);
while(top)
{
if(vis[st[top]])++cnt,dfs2(st[top]);--top;
}
for(int i=1;i<=m;i++)
{
x[i]=col[x[i]];y[i]=col[y[i]];if(x[i]>y[i])swap(x[i],y[i]);
++num[{x[i],y[i]}];
}
g.pb(cnt);
for(int i=cnt-1;i;i--)
{
// cout<<v[i][0]<<endl;
queue<int>q;
for(int x:g)if(!ind[x])q.push(x);
g.clear();
while(!q.empty())
{
int x=q.front();q.pop();g.pb(x);
if(edge(i,x))++ind[x],insert(i,x);
else
{
for(int j=lk[x],y;j;j=nxt[j])
{
if(!--cur[y=to[j]])q.push(y);
h.pb(y);
}
}
}
for(int x:g)cur[x]=ind[x];
for(int x:h)cur[x]=ind[x];
h.clear();g.pb(i);
}
ans=len;
for(int i=1;i<=cnt;i++)if(v[i].size()>1)ans+=v[i].size();
write(ans);puts("");
for(int i=1;i<=cnt;i++)
if(v[i].size()>1)for(int j=0;j<v[i].size();j++)add(v[i][j],v[i][(j+1)%v[i].size()]);
for(int x=1;x<=cnt;x++)
for(int i=lk[x];i;i=nxt[i])add(v[x][0],v[to[i]][0]);
return 0;
}
Day2
tsx 出题 + 讲课。分数:\(10+0+20=30\)
上午 T1 又是想了半天(但是很困所以其实没有想到什么很对的),然后感觉是容斥然后排除了容斥后来还是发现正解是容斥。写了 \(n^B\) 的暴力拿到了 10 分。后来用几分钟写了 T3 \(n^2\) 暴力,然后过了 \(10^5\) 没过 \(10^4\) 感觉好恶心(本题时限 10s)。T2 好像是因为我太懒了暴力都没写,算了算感觉有点难过。
听讲题,T1 果然是容斥 dp。T2 线性代数,基本上没学过。T3 有一个单次递归线段树的做法,tsx 讲的是转置原理,听到某个地方就开始掉线了,发现真没学过线性代数。后来是杂题选讲,好多没听懂的。
晚上努力写了一遍 T1 然后自己写的跟题解思路不是很一样然后寄了都不知道哪里寄了。
Day3
jsyoi 异地登录。分数:\(15+0+0=0\)
早上根本不困但是还是没写出来 T1,想了一堆但是感觉复杂度都太危险了,然后又感觉都不很正常没有写,其实我写的是 \(2^m\) 的做法但是交上去只过了第二个 sub,太诡异了,然后调了一万年,然后也没有写之前想的 \(n^3\) dp,最后获得了 15 的高分。T2 看了看想了一会然后觉得很困难,当时急着去想 T1,认为离胜利很近了,就没写也没继续想。T3 没写。
看榜,虽然每天都是被吊起来打,但是这天是特别被吊起来打,非常的难受。之前写题策略都是写着这个题看看后边的每个题都想想,但是恰好这天的 T1 不是太好想,看了眼 T2 觉得是我平时能想出来的脑筋急转弯题,但是还是认为太困难一个字都没有写。不知道为什么感觉这几天没有进行任何有效思考,特别是早上的时候。
看题解发现 T1 是逆天没有算法题。并不是之前想的逆天 dp。T2 是有意思的构造题。T3 根本没看也没想。
下午讲题,讲线性规划与网络流,刚讲两句就掉线了,昨天没看的转置就在这出现了。然后听两句听到一个没学过的就开始上网查,几乎没学什么,但是很累。
晚上写了一下 T2 的部分分。
Day4
jsyoi day2. 分数:\(10+0+15=25\)
种种原因早上略困。今天又发誓要过 T1 了,但是发现连 \(2^m\) 的暴力都想不出来我是不是完蛋了。又感觉是容斥,但是想了好多容斥相关的做法都觉得不对,非常久没有进展,只写了 \(10\) 分爆搜。T2 一眼非常麻烦的构造,先放下了。T3 获得了大众的爆搜 + 性质分。最后一个多小时乱胡了一个 T2 感觉能拿很多分的做法就开始写,写着写着发现写不完了开始瞎写。
没人过题但是依然稳定后 1/4。上午打一半心态非常崩。
下午听讲题,T1 我的思路跟正解相比非常的白痴,T3 没有想太多这题。后来讲了一些数据结构的题。
晚上写总结。
Day5
zzk 出题+讲课. 分数:\(0+0+0=0\)
保龄了,订题感觉暴力思路是如此简单。感觉考场上脑子真的有问题。
Day6
zzk 出题+讲课. 分数:\(15+0+28=43\)
获得了集训以来最高 rk。结果线下交的时候 T1 因为没复制上最后一半括号 ce 了。挂!
T1 构造题
一张无限大的网格,你可以选择上面不超过 \(X\) 个格子组成地图,共有 \(Q\) 次询问,每次在地图上选择不超过 \(Y\) 个格子,使得对于所有选中的格子,从 \((1,1)\) 走到它们的方案数之和恰好为给定的 \(k\),构造一种合法方案。(\(k\le 10^K,K\le 100\))
\(X=1000,Y=340,K=2\) (我写这一部分的时候题面上还是 \(K=2\)),这一部分是简单的,选择第一行 \([1,1000]\) 所有节点,然后每次询问选择 \(k\) 个格子,方案和显然是 \(k\)。
\(X=1000,Y=340,K=12\) ,发现 \(10^{12}\) 在二进制表示下只有(比较少)位,所以考虑弄一个这样 \(\downarrow\) 的地图(偷了题解里的图/bx/bx/bx):
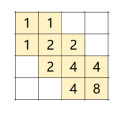
然后就可以拆分一下来做。这个做法也可以通过 sub3,但是我当时没算,以为写不了。
然后同理,转换一下进制是可以拿到更多的分的。
至于满分做法,有一个奇妙的结论,任意一个正整数都能拆分成若干个斐波那契数。然后就可以弄一个这样 \(\downarrow\) 的地图:

然后写个高精度从大到小拆一下就好了。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
ll t=0;char h=getchar();
while(!isdigit(h))h=getchar();
while(isdigit(h))t=(t<<1)+(t<<3)+(h^48),h=getchar();
return t;
}
void write(int x)
{
if(x>9)write(x/10);putchar(x%10+'0');
}
ll k;
int q,x,y,n;
struct big{
int a[110],num=0;
inline int&operator[](int i){return a[i];}
}z,K;
inline void div(big&a,int b)
{
big c=z;//cerr<<a.num<<" =w=. ";
for(int i=a.num-1;i>=0;i--)c.a[i]=a.a[i]/b,(i)&&(a.a[i-1]+=10*(a.a[i]%b));
c.num=(c.a[a.num-1]||a.num==0)?a.num:a.num-1;a=c;
}
inline big operator+(big a,big b)
{
a.num=max(a.num,b.num);
for(int i=0;i<a.num;i++)
if(a[i]+b[i]>=10)++a[i+1],a[i]+=b[i]-10;
else a[i]+=b[i];
if(a[a.num])++a.num;
return a;
}
inline big operator-(big a,big b)
{
for(int i=0;i<a.num;i++)
{
if(a[i]<b[i])--a[i+1],a[i]+=10;
a[i]-=b[i];
}
while(!a[a.num-1]&&a.num>0)--a.num;
return a;
}
char h[200];
inline void read(big&a)
{
a=z;scanf("%s",h+1);
a.num=strlen(h+1);
for(int i=0;i<a.num;i++)a.a[i]=h[a.num-i]-'0';
}
int tot=0;
inline void add(int x,int y)
{
write(x),putchar(' ');write(y);puts("");++tot;
}
void print(big x)
{
cerr<<(x.num)<<" ";
for(int i=x.num-1;i>=0;i--)cerr<<char(x.a[i]+'0');cerr<<endl;
}
inline bool operator>(big a,big b)
{
if(a.num!=b.num)return a.num>b.num;
for(int i=a.num-1;i>=0;i--)if(a[i]!=b[i])return a[i]>b[i];
return false;
}
big F[500];
struct node{
int id,x,y;
friend bool operator<(node a,node b)
{
return a.x==b.x?a.y<b.y:a.x<b.x;
}
}nd[1010];
int p[500];
bool v[1010];
int main()
{
// freopen("b.in","r",stdin);
// freopen("b.out","w",stdout);
k=read();q=read();x=read();y=read();
write(n=960);puts("");
F[1].num=1;F[1][0]=1;F[0].num=1;
p[1]=1;nd[++tot]={1,1,1};nd[++tot]={1,2,1};x=1;y=2;
for(int i=2;i<=480;i++)
{
nd[++tot]={i,x,y};if(i&1)++x;else ++y;
nd[++tot]={i,x,y};if(i&1)--x,++y;else --y,++x;
F[i]=F[i-1]+F[i-2];
}
sort(nd+1,nd+n+1);
for(int i=1;i<=n;i++)
{
p[nd[i].id]=i;add(nd[i].x,nd[i].y);
}
while(q--)
{
read(K);//print(K);
for(int i=480;i>=1;i--)
{
if(K.num==1&&K[0]==0)v[p[i]]=false;
else if(!(F[i]>K))v[p[i]]=true,K=K-F[i];
else v[p[i]]=false;
// if(v[p[i]])cerr<<"F: ",print(F[i]),cerr<<"K: ",print(K),cerr<<i<<endl;
}
for(int i=475;i>=1;i--)if(v[p[i]]&&v[p[i-1]]&&(!v[p[i+1]]))v[p[i]]=v[p[i-1]]=false,v[p[i+1]]=true;
for(int i=1;i<=n;i++)putchar(v[i]+'0');puts("");
}
return 0;
}
Day7
spx 出题+讲课. 分数:\(25+0+18=43\)
T1 只会大概 \(O(n^2)\) 预处理一下然后 \(O(1)\) 查询,后面不会了。T2 把枚举 \(m\) 条边中选 \(3\) 条的复杂度算成 \(O(3^m)\),于是一眼认定此题不可做,痛失 30 分暴力。T3 贪心获得 18 分。
下午听讲题,发现 T2 还是挺简单的,回去写了一遍暴力然后开始写正解(还没调完)。T1 是神奇的数据结构题,思维上有点太抽象了。T3 感觉也很抽象。后来讲了 FWT/FMT,努力听了一部分然后开始掉线了。
Day8
spx 出题+讲课. 分数:\(15+8+4=27\)
T1 括号序列问题一开始写了十五分暴力,然后想了一下 \(n=2000\) 的做法,差不多想完了但是后边还是有一点不会,然后去写 T2 了,后来反正还是打得很烂。
To do list
- 订题
- dp
- 脑筋急转弯(?)
- 线性代数
- 线性规划
- 多项式与生成函数
- 点分树(动态点分治)
- 单次递归线段树
- hall 定理
发现以后打模拟赛还是要注意策略,先把题都看一遍,能打的部分分先打了,然后再去想更多的分或者正解。然后就是很困的问题??


 浙公网安备 33010602011771号
浙公网安备 33010602011771号