浮点数定点表示(Q格式)

深度学习神经网络模型中的量化是指浮点数用定点数来表示，也就是在DSP技术中常说的Q格式。

Q格式

Q格式表示为：Qm.n，表示数据用m比特表示整数部分，n比特表示小数部分，共需要m+n+1位来表示这个数据，多余的一位用作符号位（不表示出来）。

例如Q15表示小数部分有15位，一个short型数据，占2个字节，最高位是符号位，后面15位是小数位，表示的范围是：-1<X<0.9999695 。

  • 浮点数据转化为Q15，将数据乘以2^15；
  • Q15数据转化为浮点数据，将数据除以2^15。

例如假设数据存储空间为2个字节，0.333×2^15=10911=0x2A9F，0.333的所有运算就可以用0x2A9F表示。

同理10911×2^(-15)=0.332977294921875，可以看出浮点数据通过Q格式转化后是有误差的。

Q格式的加减乘除基本运算

  • 加减法时须转换成相同的Q格式才能加减。
  • 不同Q格式的数据相乘，相当于Q值相加，要右移n位得到正确的值。
  • 不同Q格式的数据相除，相当于Q值相减，要左移n位得到正确的值。

这里举一个乘的例子：两个小数相乘:0.333*0.414=0.137862

// 0.333*2^15=10911=0x2A9F;
// 0.414*2^15=13565=0x34FD;
short a = 0x2A9F;
short b = 0x34FD;
short c = (a * b) >> 15; //( 十进制4516 ---> 4516/(2**15) = 0.13781)
// 两个Q15格式的数据相乘后为Q30格式数据，因此为了得到Q15的数据结果需要右移15位

这样c的结果是0x11A4=0001000110100100，这个数据同样是Q15格式的，它的小数点假设在第15位左边，即为0.001000110100100=0.1378173828125...和实际结果0.137862差距不大。或者0x11A4 / 2^15 = 0.1378173828125.

如何定标

下表是用8比特来量化的各种Q格式的值的取值范围：

Q 格式 值的取值范围
Q0.7（7 位全表示小数） [-1, 0.9921875]
Q1.6 [-2, 1.984375]
Q2.5 [-4, 3.96875]
Q3.4 [-8, 7.9375]
Q4.3 [-16, 15.875]
Q5.2 [-32, 31.75]
Q6.1 [-64, -63.5]
Q7.0 [-128, 127]

模型的量化可分为训练中量化和训练后量化，还可分为对称量化和非对称量化。

训练后对称量化为例，即先训练好用浮点表示的模型参数等，然后再去量化，量化某类值（比如weight）时看其绝对值的最大值，从而可以知道用什么定标的Q格式最合适。

模型的量化主要包括两方面的内容：各层参数的量化和各层输出的量化。

  1. 先看各层输出的量化：在评估时把测试集中各个文件每层的输出保存下来，然后看每层输出值的绝对值的最大值，比如绝对值最大值为3.6，可以从上面的8比特量化表看出用Q2.5 量化最为合适（也可以用公式 np.ceil(np.log2(max))算出整数的表示位数，然后确定小数的表示位数，从而确定定标）。
  2. 再来看各层参数的量化：参数主要包括weight和bias，这两种参数要分别量化，量化方法同上面的每层输出的量化方法一样。

Q 格式选择方法：通过 “统计最大值 + 查表 / 公式计算” 确定，两步即可落地：

  1. 统计目标数据（层输出 / 权重 / 偏置）的绝对值最大值（如某卷积层输出最大值为 3.6）；
  2. 匹配表格或用公式计算整数位：整数位数n = np.ceil(np.log2(max_val))，8bit 量化时再用 “7 - 整数位” 得到小数位（8 比特有符号数总有效位为 7，含符号位）。例如 max_val=3.6 时，log2(3.6)≈1.85，向上取整为 2 位整数，小数位 = 7-2=5，对应 Q2.5 格式，与表格中 “Q2.5 覆盖 [-4,3.96875]” 完全匹配，确保数据不溢出且精度损失最小。

关键总结

  • 8bit/16bit/32bit 的核心差异是 “有效数值位”（7/15/31），决定了小数位的上限和量化步长；
  • 相同整数位 n 下，比特数越高（如 32bit Q2.29 vs 16bit Q2.13），小数位 m 越大，量化步长越小，精度损失越低；
  • 实际选型时，优先用 “刚好覆盖 max_val 的最小整数位 n”，剩余有效位全部分配给 m（精度最大化）。
  • 若需自定义 Q 格式，按以下步骤计算范围：
  1. 确定总比特数→有效数值位 = 总比特数 - 1；
  2. 按 max_val 计算整数位 n = np.ceil (np.log2 (max_val))；
  3. 小数位 m = 有效数值位 - n；
  4. 代入公式：
    • 最小值 = -2ⁿ；
    • 最大值 = (2ⁿ - 1) + (2ᵐ - 1)/2ᵐ；
    • 量化步长 = 1/2ᵐ。

Q 格式能表示的浮点数范围和精度

举例 Q10.13 能表示的范围是多大？精度是多少?

要计算Q10.13的取值范围，需先明确其比特数属性再套用有符号定点数的通用公式推导：

第一步：确定 Q10.13 的比特数

Q10.13 的定义：n=10（整数位），m=13（小数位）

第二步：套用有符号定点数范围公式

对 Qn.m 格式的有符号定点数，取值范围公式为：

最小值 = -2ⁿ（整数位全 1、符号位为 1，小数位全 0）；

最大值 = (2ⁿ - 1) + (2ᵐ - 1)/2ᵐ（整数位全 1、符号位为 0，小数位全 1）；

量化步长 = 1/2ᵐ（最小可表示的小数单位）。

第三步：代入 Q10.13 计算具体数值

  1. 最小值

n=10 → 最小值 = -2¹⁰ = -1024。

  1. 最大值

n=10，m=13 →最大值 = (2¹⁰ - 1) + (2¹³ - 1)/2¹³= 1023 + 8191/8192= 1023 + 0.9998779296875= 1023.9998779296875。

  1. 量化步长

m=13 → 量化步长 = 1/2¹³ = 1/8192 ≈ 0.0001220703125。

最终结论

Q10.13（24bit 有符号定点数）的取值范围是：[-1024, 1023.9998779296875]，最小可分辨的小数单位约为 0.000122。

可以简记为值域为$ [-2^n, 2^n] \(**，精度为 **\) \frac {1}{2^m} $

卷积与 BN 的融合

需要注意的是如果当前层是卷积层或者全连接层，为了减少运算量，一般部署模型时都会将BatchNormal(BN)层参数融合到卷积层或者全连接层（只有当卷积层或者全连接层后面紧跟BN层时才可以融合参数，否则不可以）。

假设层的输入为X，不管是卷积层还是全连接层，运算均可以写成 $ W_{old}\times X + b_{old}
$ BN层执行了两个操作，一个是归一化，另一个是缩放，两个阶段的操作分别为：

$ \frac{X-mean}{\sqrt{var}} \
$

$ \gamma * X + \beta $

将上面三个式子合并（卷积层或者全连接层的输出就是BN层的输入, 原卷积层或者全连接层的参数为W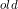和b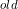），可以得到：

$ \gamma \times \frac{W_{old} \times X + b_{old} - mean}{\sqrt{var}} + \beta $

上式等于W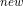 * X + b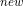，展开得到：

$ W_{new} = \frac{\gamma}{\sqrt{var}} \times W_{old} $

$ b_{new}=\frac{\gamma}{var} \times(b_{old} - mean) + \beta $

这样合并后的运算就成了：

$ W_{new}\times X + b_{new} $

在卷积层或者全连接层里用上面得到的新参数(Wnew 和 bnew)替代旧参数(Wold 和 bold)，inference时BN层就消失了。

卷积层的定标举例

卷积层或全连接层中，主要是乘累加运算，通常格式是$ output=\sum {input \times weight} + bias $。

  • 这里input是当前层的输入（即是上一层的输出）
  • weight是当前层的权值
  • bias是当前层的偏置
  • output是当前层的输出。

这四个值均已定标，在运算过程中要想得到正确的结果，需要做移位处理。怎么移位呢？下面举例说明。

假设input定标为Q5.2，weight定标为Q1.6 ，bias定标为Q4.3 ，output定标为Q2.5。假定只有一个input和一个weight。

  • input浮点值是28.4，用Q5.2 表示就是01110010 （28.4 *22 = 113.6，四舍五入就是114）；
  • weight浮点值是1.6，用Q1.6 表示就是01100110；
  • bias为12.8，用Q4.3 表示就是01100110；
  • Input * weight = 01110010 * 01100110 = 0010 1101 0110 1100 = 11628(十进制表示)。

八位数乘以八位数超出了8位数的表示范围，要用16位表示。28.4 * 1.6 = 45.44，要让11628表示45.44，所以11628用Q7.8 表示（11628 / 45.44 约为256 = 28 ）。从上面计算看出，两个八位数相乘是16位数，16位数的定标小数位数是两个8位数的定标小数位数相加。这里Q7.8 中的8是Q5.2 中的2加上Q1.6 中的6。定标小数位数知道了，整数位数就是（15 - 小数位数），这里小数位数是8，整数位数就是7（7 = 15 - 8）。

不同定标的数也不能直接相加，所以要把bias的Q4.3 表示的值转换成Q7.8 表示的值。Bias原始为12.8，用Q4.3 表示就是12.8 * 23，用Q7.8 表示就是12.8 * 28 。可以看出bias从Q4.3 转变为Q7.8 ，只要乘以 25 即可，即左移5位。

再来看上面的式子output = input*weight + bias，等式右边经过计算后变成了Q7.8 ，而等式左边是根据非常多的样本算出来的层的输出的绝对值的最大值得到的定标Q2.5 ，所以最后要把Q7.8 格式转换成Q2.5格式 。对于一个浮点数，假设为a，用Q7.8 表示就是a * 28 ， 用Q2.5 表示就是a * 25 ，可以看出要把Q7.8 格式转换成Q2.5格式 ，只需右移3位（3 = 8 - 5）即可。

所以再总结一遍每一层计算过程中移位的处理如下：

  • 假定input定标为Qa.b
  • weight定标为Qc.d
  • bias定标为Qe.f
  • output定标为Qm.n

这些值均为8比特表示，即a+b=7，c+d=7，e+f=7，m+n=7。

input * weight 为16比特Qu.v表示，其中v=b+d，u = 15 - v。

计算过程中要把bias从8位表示变成16位表示，若f<v，bias则要左移(v-f)位，若f>v，bias则要右移(f-v)位，若f=v，则不移位。

处理后input*weight + bias是一个16位表示的数，而output是一个8位表示的数，还要把16位表示的数转换成8位表示的数。若n<v，16位表示的数则要右移(v-n)位，若n>v，16位表示的数则要左移(n-v)位，若n=v，则不移位。

评估标准

按照上面的方法，各层的模型参数以及输出都量化好了。量化好后还要对量化进行评估，评估的指标是余弦相似度和欧几里得距离等。余弦相似度是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似。公式如下：

\[cos(\theta) = \frac {\sum^n_{i=1}(x_i \times y_i)}{\sqrt{ \sum^n_{i=1}(x_i)^2} \times \sqrt{ \sum^n_{i=1}(y_i)^2}} \]

欧几里得距离，又称欧氏距离，是最常见的距离度量，衡量的是多维空间中两个向量之间的绝对距离。欧氏距离越小，相似度越大；欧氏距离越大，相似度越小。公式如下：

\[d(x,y):=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2} = \sqrt{\sum^n_{i=1}(x_i-y_i)^2} \]

评估时要一层一层的评估，用余弦相似度和欧几里得距离等比较每层的量化前浮点的输出的向量和量化后的定点的输出向量（定点的输出向量算好后要根据定标转成浮点数才能比较）。余弦相似度要接近1和欧几里得距离要接近0，才是一个合格的量化。否则要找出量化中的问题，直到指标达标。

posted @ 2025-11-27 19:52  白柒  阅读(0)  评论(0)    收藏  举报