浮点数误差的原因
Ⅰ.引入
Python,C,都能得到一个反直觉的结果,0.1 + 0.2 == 0.3 返回的是 false。本文将从 0.1 + 0.2 展开,解释为什么浮点数的计算存在误差,并提供一种简单的估计误差的方法,期望在编码时,这个方法能帮我们提前考虑到计算误差的风险,并在设计时尽量规避这样的风险。
精度问题无法解决
浮点数表示这里有一个无法解决的问题,数学中任意小段连续的数轴中的小数就是无限的,这意味着我们需要无限个互不相同的零一序列(一对一的映射)才能表示。但是,现实的计算机中,我们没有无限的内存,有限的内存就意味着我们只能表示有限的数字。简单而言,从数学角度说,无论任何浮点数标准,都面临用有限的集合去映射无限的集合的问题,都一定会存在精度问题。
Ⅱ.误差产生原因
1.进位制编码造成的误差
与整数不同,因为浮点数在计算机中的存储方式(IEEE754),浮点数无法精确表示有效范围内的所有数值。有效范围内的数值是否可以被精确表示取决于有效数字fraction是否可以被完全存储。例如3.5可以被精确存储,3.6无法被精确存储。

其中,最高位一位是符号位sign,用于区分正负(0正1负),中间 exponent (8位)代表指数部分,低位 fraction/尾数存储有效数字。以十进制的$ 1.12 \times 10^2 $为例,可以形象地理解fraction(.12)决定了数字是哪个数字,exponent(2)决定了小数点在哪。我们可以用「有效位」代指 fraction 所占用的存储空间(23bit),用「浮点位」代指 exponent 所占用的存储空间(8bit)。
把十进制小数8.26转换成二进制,具体应该怎么操作?
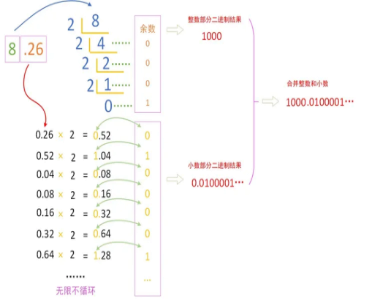
整数部分+小数部分得到二进制结果为1000.0100001 …
根据IEEE754标准,即符号位+尾数+阶码的计数方式,可以表示为$ 1.0000100001 × 2 ^3 $。其中
- 符号位:0
- 阶码部分:以float为例子,则为 127+(3)=130,所以二进制为:10000010
- 尾数部分:0.0000100001...,它本身无限不循环,以 float 为例,截取 23位,表示为00001000010100011110110
最终结果为(以二进制表示)
:::tips
01000001 00000100 00101000 11110110
:::
因此,对于这种无限位数的小数,用计算机去存储必然会导致精度的损失。
2.运算上的误差
在C语言中,float类型的数据范围是从[1.17549435e-38, 3.40282347e+38],如果超出了这个范围,就会发生溢出。系统会将数值设置为特殊值来表示溢出情况,通常是正无穷大或负无穷大。这个特殊值会被传递给相关计算,以避免无效的运算结果。浮点数溢出通常会触发一个异常或警告,表示计算结果已经不再可靠。
3.平台误差
不同平台处理浮点的算法不一致,会导致运算结果不一致。存在这几个方面:
- 编码规则,这个IEEE一般都是有颁布运算标准的,这个部分基本是已经标准化了
- 舍入方式:其实是规则的一部分,但是IEEE自己也保留了好几套舍入方式
- 硬件:具体的就是,浮点寄存器的位宽。比如IBM提供过一个拓展,可以将float拓展到80bit, 那么用了这个拓展和不用,就会导致精度的不同。
- 平台对float设置和优化不同:如微软的/fp指令。(https://docs.microsoft.com/en-us/cpp/build/reference/fp-specify-floating-point-behavior?view=msvc-170)
4.类型转换导致的误差
如果转换能将原有的信息完全保留(比如int转long,而long包含了所以int能表示的数和不能表示的数),这种隐式转换(implicit conversion)。而反过来显式转换(explicit conversion)可能会信息丢失造成误差,比如 int a = (int)10.0f。
Ⅲ.浮点数误差的应对
单精度浮点数(float)总共用32位来表示浮点数,其中尾数用23位存储,加上小数点前有一位隐藏的1(IEEE754规约数表示法),$ 2^{23+1} = 16777216 \(。因为\) 10^7 \lt 16777216 \lt 10^8 $ ,所以说单精度浮点数的有效位数是7位。考虑到第7位可能的四舍五入问题,所以单精度最少有6位有效数字(最小尺寸)。 通常认为单精度浮点数的有效数字是6~7位,绝对可以保证的是6位。
// float的有效数字是6或7位,第7位不一定有效,前6位一定有效。
float f = 3.123456;
printf("%f",f);// 可靠数据是前6位,即3.12345。
float f = 123456.789
printf("%.2f",f);//要求输出结果保留两位,但是这两位小数保留的毫无意义
float f = 1234560.991f;
printf("%f",f);//输出结果是1234561.000000
float f = 1.913757f;
printf("%.10f",f);//输出结果是1.9137569666,只有5位小数是精确的。
综上,所以精确度是6位,意思是前6位一定精确,6位以后的可能精确,可能不精确。
以想要保留小数点后两位有效数字为例,那么单精度浮点数整数部分可以使用的最大值是多少呢?要保证小数点后两位小数有效,即需要保证的精确度为0.01。frac共23位,第一位代表$ 2^{-1}=0.5 \(,第二位代表\) 2^{-2}=0.25 \(,依次类推,第六位代表\) 2^{-6}=0.015625 \(,第七位代表\) 2^{-7}=0.0078125 \(,即至少需要7位小数域才能精确表示0.01。规格化浮点数有效数字域共23位,加上1默认占有的1位,共24位表示有效数字。小数部分需要占有7位有效数字域,那么整数部分占有位数为\) 24-7=17 \(位。\) 2^{17}=131072 $,即保留小数点后两位,单精度浮点数整数部分最大可以使用131071,超过该数值后,小数点后两位就无法被精确表示。
| 精度 | 0.1 | 0.01 | 0.001 | 0.0001 | 0.00001 | 0.000001 | 0.0000001 |
|---|---|---|---|---|---|---|---|
| 整数最大值 | 1048576 | 131071 | 16384 | 1024 | 128 | 16 | 1 |
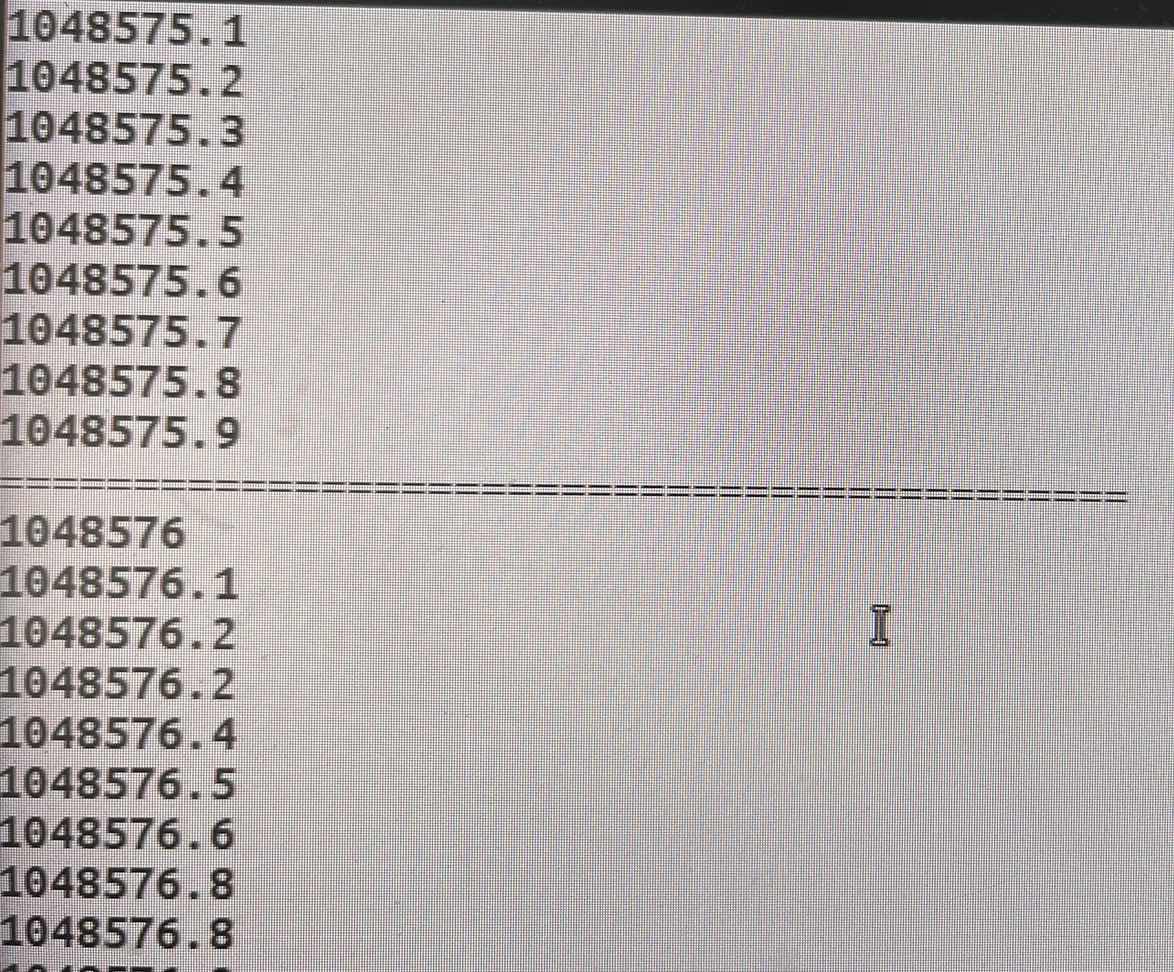
利用setprecision函数可以验证以上数值:
// setprecision(8) 会控制输出的有效数字为8位
cout<<setprecision(8)<<1048575.0f<<endl;
cout<<setprecision(8)<<1048575.1f<<endl;
cout<<setprecision(8)<<1048575.2f<<endl;
cout<<setprecision(8)<<1048575.3f<<endl;
cout<<setprecision(8)<<1048575.4f<<endl;
cout<<setprecision(8)<<1048575.5f<<endl;
cout<<setprecision(8)<<1048575.6f<<endl;
cout<<setprecision(8)<<1048575.7f<<endl;
cout<<setprecision(8)<<1048575.8f<<endl;
cout<<setprecision(8)<<1048575.9f<<endl;
printf("===========================================\n");
// 以下输出不能按预期打印
cout<<setprecision(8)<<1048576.0f<<endl;
cout<<setprecision(8)<<1048576.1f<<endl;
cout<<setprecision(8)<<1048576.2f<<endl;
cout<<setprecision(8)<<1048576.3f<<endl;
cout<<setprecision(8)<<1048576.4f<<endl;
cout<<setprecision(8)<<1048576.5f<<endl;
cout<<setprecision(8)<<1048576.6f<<endl;
cout<<setprecision(8)<<1048576.7f<<endl;
cout<<setprecision(8)<<1048576.8f<<endl;
cout<<setprecision(8)<<1048576.9f<<endl;
1.估计方法
为了估计系统面临的误差风险,我们需要估计如下三个量,然后结合浮点数有效位的限制,做出估计:
- a - 系统中可能涉及的最大整数数值
- b - 系统要求的精度(比如小数点后 6 位)
- c - 系统的运算规模
- n - 浮点数有效位的位数
然后通过下述公式计算,log以2为底
$ n+1 \leq log_2a + log_2b + log_2c $
我们可以简单体验一下这个公式,假设我们系统中可能涉及的最大整数不超过一亿,系统要求小数点后 6 位都是精确的,我们可以简单计算 loga + logb(10**6) 并向上取整得到 47,这表明我们需要 47 位都是精确的。假设我们使用 64 位双精度浮点数标准,此时 n = 52,根据上述公式我们,我们可以判断,在最坏的情况下,计算次数超过 64 次,便有可能导致最后一位(第 6 位)小数不精确。如果我们只要求 2 位小数精确,我们可以再次计算,此时精确位只需要 34 位,此时计算规模不超过 2^19 时,我们的系统都能保证精确。
如果上述不等式成立,则系统面临误差风险,右侧比左侧超出的越多,则出现不可接受范围的误差的可能性越大。
2.应对方法
在进行浮点数计算时,精度损失是不可避免的,但可以通过一些方法来尽可能地减少精度损失。
- 利用算术运算法则,将算式转换为更加稳定的计算方式。例如,可以将 A/B * C 转换为 A * (C/B),或者将 A/C * B 转换为 A * (B/C)(当已知B/C为整数时)。
- 使用高精度库(如 GMP、MPFR 或BigDecimal,Decimal等)或自定义实现高精度运算的数据结构,来代替原本的浮点数类型进行计算。double类型具有更高的精度,可以减少精度损失;使用BigDecimal类型可以获得更高的精度和更好的控制。
- 按照从小到大的顺序进行相加。这样可以保证较小的数字先被相加,减少误差的传递。
Ⅳ.实验
float arr[16];
int low = 3, high = 100;
for(int i=0; i<16;i++){
float n = low + static_cast<float>(rand()) * static_cast<float>(high-low) / RAND_MAX;
arr[i] = n;
}
v16f32 vinputs = _mx512_lao(vinputs, 0, arr, 0);
vinputs = _mx512_lao(vinputs, 1, arr, 1);
v16f32 vsum = _mx512_fxas8w(vinputs);
vsum = _mx512_fxas4w(vsum);
vsum = _mx512_fxas2w(vsum);
vsum = _mx512_fxas1w(vsum);
printf("vsum: %f\n", vsum[0]);//990.198242
float compare1_src(float *arr){
float sum = 0.0f;
for(int i=0; i<16; i++){
sum += arr[i];
}
return sum;
}
float compare2_src(float *arr){
float sum = 0.0f;
float sum0_8 = arr[0] + arr[8];
float sum1_9 = arr[1] + arr[9];
float sum2_10 = arr[2] + arr[10];
float sum3_11 = arr[3] + arr[11];
float sum4_12 = arr[4] + arr[12];
float sum5_13 = arr[5] + arr[13];
float sum6_14 = arr[6] + arr[14];
float sum7_15 = arr[7] + arr[15];
float sum08_412 = sum0_8 + sum4_12;
float sum19_513 = sum1_9 + sum5_13;
float sum210_614 = sum2_10 + sum6_14;
float sum311_715 = sum3_11 + sum7_15;
float sumA = sum08_412 + sum210_614;
float sumB = sum19_513 + sum311_715;
return sumA + sumB;
}
float sum_tmp;
_mx512_saw(vsum, 0, &sum_tmp, 0);
printf("vsum: %f 0x-> %x\n", vsum[0], *((uint32_t*)&sum_tmp));
float sum1 = compare1_src(arr);
printf("sum1: %f 0x-> %x\n", sum1, *((uint32_t*)&sum1));
float sum2 = compare2_src(arr);
printf("sum2: %f 0x-> %x\n", sum2, *((uint32_t*)&sum2));
printf("%d, %d\n", vsum[0] == sum1, vsum[0] == sum2);
/*
*vsum: 990.198242 0x-> 44778cb0
*sum1: 990.198181 0x-> 44778caf
*sum2: 990.198242 0x-> 44778cb0
*0, 1
*/
Ⅴ.附录
浮点数转换二进制工具: IEEE-754 Floating Point Converter


 浙公网安备 33010602011771号
浙公网安备 33010602011771号