一文搞懂补码

一文搞懂补码

前言

​ 在学习计算机组成原理时经常接触到补码，我们知道计算机使用补码来表示负数，并且负数的补码按位取反再加一是他对应的正数。但是我们往往知道的也就仅限于此，其原理和原因似乎不被重视。像这样对一些概念浮于表面的后果就是，当涉及到这个概念更深层次的问题时，我们原有的理解就会变得促膝见肘，一些现象无法从已有的知识解释。而当我们再次深层次的去挖掘原理时，就会发现，其背后往往是数学在施展魔法。

如何用加法代替减法

​ 首先，为什么计算机不直接计算减法？如果计算机在底层可以直接进行两个数的减法计算，那么就不需要补码什么事了。原因也很简单，纯粹的二进制减法实现起来相当复杂。而使用补码可以将减法通通转化成加法计算，CPU 对于执行加法运算非常快速且简单，而且如此一来计算机就可以透明的计算加减法。

表盘模型

​ 那么，怎么实现加法代替减法呢？我们可以参考时钟的表盘。

​ 假如我们有 0～9 共 10 个数，他们被均匀刻在一个表盘上：

我们可以在上面取到 0 ～ 9 共 10 个刻度（每个刻度表示某个范围内的每个整数，比如0~255，这里简便起见只考虑 0~9），表盘上的指针可以从一个刻度拨动到下一个刻度。从任意一个刻度朝固定方向连续移动 D = 10 次，指针将再次指向出发刻度。现在我们讨论如何在上面表示负数。假设在圆盘上从 0 刻度顺时针移动一次，有 a = 1 （a 指向刻度 1）如下图：

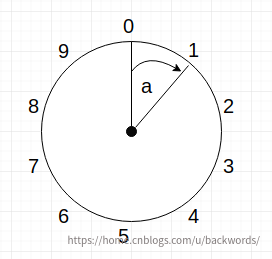
现在我们想知道，如何表示 \(-a\) （即 -1）？因为这里的指针移动是有方向的（顺时针、逆时针），所以你肯定会说，从 0 反方向移动一个刻度，即为 \(-a\) 。没错，不过我们暂时不这样考虑。我们先来想这样一件事，若有一个值属于 0 ～9 能代表 \(-a\) ，那么它与 a 的加和是为 0 的（注：加和为 0 在这里的体现是 a 再次移动某次后，指向 0 刻度），现在我们观察这个表盘，a 已经移动了一个刻度，如果想让它移动到 0 刻度，有两种方法，一是之前说过的反向移动一个刻度。另一种就是继续向前移动 9 个刻度，回到 0 刻度。两种方法都可以回到 0 ，不过我们不考虑第一种，因为它不方便表示。

示意图：

现在考虑如何表达第二种移动方法，很显然，我们可以将它表述为：\(a + （表盘总共可移动次数 - a) = 0\)(刻度) ；即 \(a + (D-a) = 0(刻度)\) ；可以看到，我特意强调了这里的 0 是刻度，如果你将 \(D = 10\) 带入上式，你会得到一个结果 10，但这却和上式矛盾。原因是上式计算的是最后指针指向的刻度，而不是移动的次数。如果将上式做一下化简，就会得到式：\(D = 0(刻度)\) 。可能看起来有些奇怪，再对其变型：\(0 + D = 0(刻度)\) ；该式含义为从 0 刻度移动 D 次（10次），将再次回到 0 刻度。虽然这种说法很合理，但是计算机可没有给我们提供关于刻度的计算，\(0 + D\) 从数值上就是等于 D，即为 10。所以为了让数值计算上满足我们的刻度计算的结果，我们可以使用 取模 运算来模拟这种在表盘上的刻度移动运算：$$[a + (D - a)] % D = (D) % D = 0$$ ；

注意到这里的 \(D-a\) 数值上等于 10 -1 = 9，带入上式后：\(a + (-a) = [a + (D-a)]\%D = (a + 9)\%D = (10)\%10 = 0\) ; 即规定了这种运算后，我们就可以用 9 来代表\(-1\)，用 \((D-a)\%D\) 来代表 \(-a\)。然后我们也可以惊喜的发现，由于我们使用一个正数表示某个数的负数，在我们规定的运算规则下，两个数的减法运算似乎被我们变成了两个数的加法运算OVO！。

注意，一旦我们使用 9 来代表 \(-1\) ，那么 9 便只能作为 \(-1\) 参与运算，我们无法再取得 9 ，因为他已经有其他用途了。所以，原取值范围将缩一半，0~9 的范围可能就变成了 0~4 的取值范围，剩下的数 5~9 用来表示 0~4 对应的负数 。 接下来计算在 0~9 范围内的每个数的负数表示：

对于这个表盘来说，当 a 取 0 时，0 无正负（补码 0 无符号），所以 0 仍代表 0；

当 a 取 1 时，\(-a = (D-a)\%D = (10-1)\%10 = 9；即 -1 = 9\) ;

当 a 取 2 时，\(-a = (D-a)\%D = (10-2)\%10 = 8；即 -2 = 8\) ;

当 a 取 3 时，\(-a = (D-a)\%D = (10-3)\%10 = 7；即 -3 = 7\) ;

当 a 取 4 时，\(-a = (D-a)\%D = (10-4)\%10 = 6；即 -4 = 6\) ;

当 a 取 5 时 ，\(-a = (D-a)\%D = (10-5)\%10 = 5；即 -5 = 5\) ; （5 使用 5 本身来表示自己的负数？先跳过）

a 无法再取更大的值，因为 6 已经被作为 \(-4\) 看待，我们的正数范围只能取到 5 。分配完正负角色后的表盘如下图所示（黑色 0 非正非负，红色为正数，蓝色为负数，绿色可正可负）：

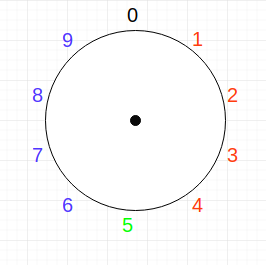
初始时我们可以在表盘上取到的值是 0~9，当使用一部分的值作为负数使用后，原来的值的绝对值范围将缩小，这里在分配完正负后，其范围为 \([0,5] \cup [-1,-4]\) ；\([0,4] \cup [-1,-5]\)。为表述方便，我们之后称这些用来表示另一个正数的负数的数 为对应正数的 补数。

现在我们来简单验证一下，在规定模运算下，减法运算到加法运算转换的正确性：

\(1-1=(1+9)\%10 = 0\);

\(2-2 = (2+8)\%10 = 0\)；

\(3-3=(3+7)\%10 = 0\);

\(...\)

\(3-2=(3+8)\%10=1\);

\(4-1=(4+9)\%10=3\)；

\(...\)

工作的很好:)。

二进制的情形

现在来考虑计算机中二进制数的情形，并考虑在此情形下如何将减法等效为加法。

现设有 8 位二进制数，它的取值个数有 \(2^8\) 个，所以取值范围为：即 \(0 ～ 255\) 。同我们之前讨论的一样，如果我们将这 256 个数均匀分布到一个表盘上，那么同样可以得到一个满是刻度的表盘：

这里 D 取 \(2^8=256\)，根据之前的讨论，我们可以很容易得出在这个范围上，可以使用 128 ~ 255 这 128 个数表示 0 ~ 127 对应的 128 个负数，并通过取模运算从而实现减法变为加法运算。你可能注意到，之前在我们的 0~9 表盘上，5 的位置是绿色的，我也提过，5 是可正可负的，因为它的正负并没有严格要求，因为我们 透明 的处理加法和减法，无论是加 5，还是减 5，作为加法取模运算后，结果都是正确的。\(5-5\) 和 \(5+5\) 最后都会变成 \((5+5)\%D\) 来计算。而现在我们的例子，128 被认为是代表一个负数（即一个正数的补数），至于为什么，稍后会解释。

接下来让我们考虑一下当这些数为二进制的形式时的情况。

通过之前的结论，我们可以如此举例： 45 的负数为 \(D-45 = 256 - 45 = 211\) ，将他们分别用二进制形式表示：

十进制	二进制
45	0010 1101
211	1101 0011

因为 \(45 - 45 = 0 = (45+211)\%D\) ；使用二进制形式表示（下面过程没有使用模运算）：

0010 1101 - 0010 1101 = 0000 0000 
= 0010 1101 + 1101 0011 = 
    0010 1101
  + 1101 0011
 -------------
   10000 0000

注意这个结果，它有 9 位，显然已经超出 8 为二进制数，所以得到溢出后的结果：0000 0000。没错，无需任何附加运算，只需要简单的将一个数与它的补数相加，CPU 将得到两个数的差值。这就是计算机中，实现负数的方式。而一旦有了负数的正数表示形式，那么减法自然可以转化为加法进行计算。

二进制补数计算

那么紧接着的另一个问题也就随之而来，怎么知道每个数的补数呢？我们之前是通过这种方式计算的：

\(-a = (D-a)\%D\) ；对于给定范围内的每个数都带入这个公式计算一次吗？从算法上来讲，是的。但是从实现上来讲，计算机有更高效的方法来实现这个操作。找到一个二进制数的补数，等价于找到一个数与原数加和后，最高位发生溢出，其余位为 0。那我们自然想到，一个二进制数，如果全为 1 的话，再将其加 1，那么最高位就自然溢出，并清零了所有的位。那么怎么获得全 1 的二进制数呢？考虑二进制数：

0010 1101；想要该数与一个数加和为全 1 ，那么该数必然将原数所有的 0 都变为 1，而原来的1 保持不变，所以我们得到一个二进制数：1101 0010；仔细一看，没错，原数的反码。此时将两数加和得到的全 1 二进制数加 1，即得到 8 位全 0 的结果。上述过程就是计算机求解一个二进制数__补码__ 的过程，而计算机使用补码来表示一个二进制正数的负数形式。

表示范围

接下来我们讨论 0~255 这个范围中，哪些作为正数，哪些作为补数存在。

毫无疑问，正数是要从 1 开始枚举的（0是正数），每次枚举一个数，我们相应的可以计算出他的一个补数，直到我们遇到了正负数形式相同的 128。（对应之前 0~9 范围的 5）

128 应该划分为正数还是负数（正数的补数）？之前我们直接给出了结论，现在来说明为什么。

如果你将 0 ～ 255 这 256 个数使用二进制形式全部枚举出来，你将得到两堆数，第一堆是最高位 0 开始的：0000 0000 ～ 0111 1111，表示范围 0~127，而另一堆是最高位以 1 开始：1000 0000 ～ 1111 1111，对应范围 128 ～ 255；计算机似乎发现了一个绝妙的方法用来辨识一个二进制数的正负，那就是查看最高位，如果一个（有符号）二进制数最高位为 1 ，那么就认为它代表一个负数，如果最高位为 0 ，那么它就为一个正数。这种规则简单且高效。唯一的问题就是，一旦应用这种规则，那么我们之前疑惑的 128 （1000 0000），就不得不成为一个补数了。不过这样也很优雅，将表数范围正好分为两个相等的部分，

0 和 正数共 128 个数，范围 \(0～127\) （0000 0000 ～ 0111 1111）；

补数（表示负数）128 个，范围 \(-128～-1\) （1000 0000 ～ 1111 1111）；

将他们分布到一个表盘上：

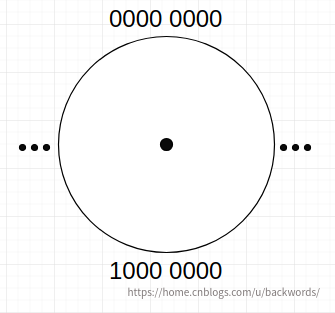
从 0000 0000 （表示 0） 顺时针旋转，正数取值不断变大，直到与 1000 0000 右侧紧邻的 0111 1111 （表示正数 127）。

从 1000 0000 （表示 -128）顺时针旋转，负数取值不断变大，直到 0000 0000 左侧紧邻的 1111 1111（表示负数 -1）。

后记

写这篇文章之前，我以为我真的懂了补码的概念，可当我真正想努力给别人阐述清楚我是怎样想的和事实应该是怎样的时候，我发现，我知道的与我以为我知道的，相差很多。我不能简洁明了的表达我所想的，可能是文笔不行，也有可能是我只是多知道了一点，却以为是一个飞跃，然后试图将这个飞跃真实的描绘出来。而实际呢，恐怕是一个残缺、粗糙的模型，在脑海中丰满无比，一旦将其一丝不苟的描述出来，就会发现竟是漏洞百出。可能我们总是喜欢乐观的高估自己吧（能力错觉）。当然完成这篇文章后，我也收获了比预期更多的东西。

去写作也许就是基于这样的目的，能真切的让人认清自己，与自己对话，沉淀自己，变得凝实，避免虚浮。

修修改改写了好几天，总觉得逻辑似乎有些问题。如果有什么问题，欢迎指正。

作者：Skipper
出处：https://www.cnblogs.com/backwords/p/10877323.html
本博客中未标明转载的文章归作者 Skipper 和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。