AT_arc191_d

可能更好的阅读体验

题意：给定一张简单无向图，一开始有两个棋子分别在 \(S,T\)，每次操作可以选择某个棋子并将其移动到相邻的点上，但是任意时刻两个棋子都不能相遇，求使棋子位置交换所需的最小操作次数，无解输出 -1。

下称答案为 \(ans\)，\(S,T\) 之间最短路长度为 \(d\)，次短路长度为 \(se\)，点 \(u\) 的度数为 \(deg_u\)。

容易想到 \(ans=d+se\)，但是次短路可能会直接在最短路的基础上选择一条边绕，得到 \(ans=2d+2\)，然而这样的方案是不合法的。换句话说，只有 \(se=d\) 或 \(se=d+1\) 时 \(ans=d+se\) 才合法且最优。

当 \(se\ge d+2\) 时，我们发现：在最短路（除 \(S,T\)）上选择点 \(u\)，那么只要 \(deg_u\ge 3\)，就一定存在与 \(u\) 相连且不在路径上的边，在这条边上绕一下就能得到 \(ans=2d+2\)。

如果找不到这样的点 \(u\)，则最短路一定是一条链。一个显然的想法是将这条链删掉后再求一次最短路并与 \(d\) 求和，但可能还有下图这种情况：

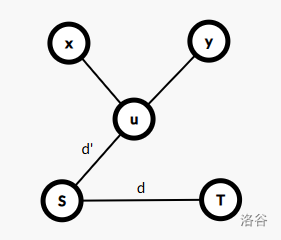
对应方案：

将 \(S\) 处的棋子移动到 \(x\)。

将 \(T\) 处的棋子移动到 \(y\)。

将 \(x\) 处的棋子移动到 \(T\)。

将 \(y\) 处的棋子移动到 \(S\)。

这也说明，我们可以不在最短路（除 \(S,T\)）上选择点 \(u\)，只要 \(deg_u\ge3\)，就存在如上图所示的方案。设 \(u\) 到 \(S\) 距离为 \(d'\)，则总操作次数为 \(2d+4d'+4\)，当然可以调换 \(S,T\) 的顺序。

于是就分讨完了，时间复杂度 \(O(n)\)，整理后的代码提交记录。