在单链表中寻找环路问题

问题1：

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。返回bool型

问题升级：

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。返回指向相交节点的指针型Listnode*

关于问题1和问题2存在用哈希表的思维解题，但可想而知，实现较为麻烦，所以寻找另一种可行的解题思路

引入快慢两个指针，每一次，其中一个指针走一步，另一个指针走两步，如果最终他们会在某一节点相遇，证明存在环，否则循环不下去的都为false；代码如下：

一定要注意不要用到空指针

bool hasCycle(ListNode *head) {
        ListNode* L1=head;
        ListNode* L2=head;
        if(head==NULL || head->next==NULL)
            return false;
        while(L1->next && L1->next->next && L2->next) //这里加上L1是怕出现空指针的情况
        {
            L1=L1->next->next;
            L2=L2->next;
            if(L1==L2)
                return true;
        }
        return false;
    }

对于问题的升级，我们不仅仅要判断其有没有环，还要判断该入环点的位置，并返会该入环点。

在没有环路存在的时候问题的处理思路一样，返回NULL即可，但是如果一经发现有环，那么接下来可以将L1和head指针一步一步向下遍历，直到相遇，即为结果

分析：假设在入环点前要走F步，环长为X。首先假设这个环非常大，远远大于F

辅助图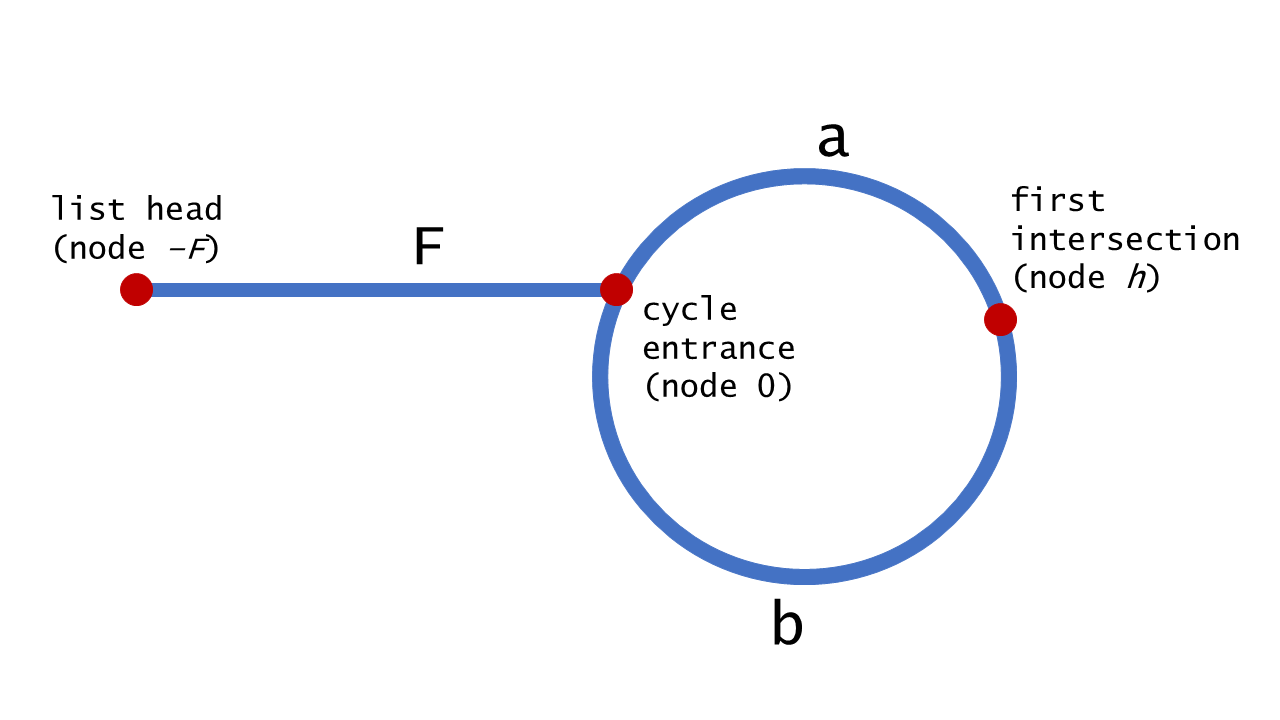：　图中a替换成F，b替换成X

 

 

 

两个快慢指针从开始到相遇要经历如下几个阶段

1.慢指针走F/2步，快指针走F步，快指针入环

2.慢指针再走F/2步，慢指针也走到了入环口，快指针走F步，快指针在入环后又走了F步，我们提前假设过，X远远大于F，所以快指针依旧在环中

3.令a=X-F，a即为快指针在入环后走了F步，还需走a步才能再次到达入环口；

4.慢指针从入环口走a步，快指针从F处走2*a步，即快指针走a步到达入环口后又走了a步与慢指针相遇。

5.我们知道a是X-F，那么走了a步的位置，不难想象相遇点离环的入口距离F步。出发点和相遇点都离该入口具有F步，遍历相遇即可。

好，现在这种环特别大的假设已经成立了，环如果特别小呢？在环很小的时候，可以知道快指针无限循环了非常多次该环才与慢指针相遇，这些小环完全可以拟看作一个大环，道理同上。

代码如下：

ListNode *detectCycle(ListNode *head) {
        ListNode *L1=head;
        ListNode *L2=head;
        if(head==NULL || head->next==NULL)
            return NULL;
        while(L1->next && L1->next->next && L2->next)
        {
            L1=L1->next->next;
            L2=L2->next;
            if(L1==L2)
            {
                ListNode *L=head;
                while(L1!=L)
                {
                    L=L->next;
                    L1=L1->next;
                }
                return L;
            }
        }
        return NULL;
    }