抛硬币直到连续若干次正面的概率

问题

 
 
  1. 假设有一个硬币，抛出字（背面）和花（正面）的概率都是0.5，而且每次抛硬币与前次结果无关。现在做一个游戏，连续地抛这个硬币，直到连续出现两次字为止，问平均要抛多少次才能结束游戏？注意，一旦连续抛出两个“字”向上游戏就结束了，不用继续抛。  

上面这个题目我第一次见到是在pongba的TopLanguage的一次讨论上，提出问题的人为Shuo Chen，当时我给出了一个解法，自认为已经相当简单了，先来考虑一下抛硬币的过程：首先先抛一枚硬币，如果是花，那么需要重头开始；如果是字，那么再抛一枚硬币，新抛的这枚如果也是字，则游戏结束，如果是花，那么又需要重头开始。根据这个过程，设抛硬币的期望次数为T，可以得到关系

　　T = 1 + 0.5T + 0.5( 1 + 0.5 * 0 + 0.5T)

解方程可得到 T = 6. 由于上面这个方法只能得到期望，而无法得到方差以及具体某个事件的概率，后来我又仔细分析了一下，推出了概率生成函数为（推导的过程暂时略过，后面你会看到一个更一般、更简单的推导）

　　

于是可以算出方差 V = G''(1) + G'(1) - G'(1)^2 = 22。将G(z)根据Rational Expansion Theorem [CMath 7.3]展开，可以得到需要抛n次硬币的概率为

　　

其中Fn是Fibonacci数列的第n项。到这里，我觉得这个问题似乎已经完全解决了，直到昨天看到Matrix67的牛B帖。在此帖中Matrix67大牛用他那神一般的数学直觉一下将需要连续抛出n个字的一般情形给解决了，而且得出的结果相当简洁：Tn = 2^(n+1) - 2，其中Tn为首次出现连续的n个字的期望投掷数。这也给了我一些启发，我试着将上面的过程进行推广，居然得到一个简单得出人意料的解法（甚至比上面n=2的推导过程还简单）。这个解法的关键在于下面这个递推关系

　　Tn = Tn-1 + 1 + 0.5 * Tn

也即是有 Tn = 2 * Tn-1 + 2。由于 T1 = 2，因此可以得到 Tn = 2^(n+1) – 2。上面的递推关系是怎么来的呢，一个直观的理解是这样的：首先先抛掷Tn-1次，得到连续的n-1个字，然后再抛一次，若是字，则游戏结束；否则需要重头开始，也就是说又需要 Tn 次。

期望投掷次数已经得出来了，但是我们还想知道方差、恰好需要投掷 m 次的概率等其它一些更具体的性质。为了方便理解概率的分布情况，我先用程序生成了一个概率表如下所示。在下表中，第n行、第m列的元素为 Pnm，表示首次出现连续n个字的投掷数为m的概率。

1/2 1/4 1/8 1/16 1/32 1/64 1/128 1/256 1/512 1/1024
0 1/4 1/8 2/16 3/32 5/64 8/128 13/256 21/512 34/1024
0 0 1/8 1/16 2/32 4/64 7/128 13/256 24/512 44/1024
0 0 0 1/16 1/32 2/64 4/128 8/256 15/512 29/1024
0 0 0 0 1/32 1/64 2/128 4/256 8/512 16/1024

仔细观察上表，你发现什么有趣的性质没？如果忽略掉分母的话，那么第n行恰好是一个n阶Fibonacci数列。例如可以考查各行的最后一列，有

第一行：1 = 1

第二行：34 = 21 + 13

第三行：44 = 24 + 13 + 7

第四行：29 = 15 + 8 + 4 + 2

第五行：16 = 8 + 4 + 2 + 1 + 1

怎么解释这个现象呢？我们再来仔细考虑一下掷硬币的过程，为方便在下文中用1表示字，用0表示花，于是我们的目标是要恰好使用m次投掷，得到连续的n个1.

若第一次的结果为 0，那么剩下的任务就是恰好使用m-1次投掷得到到连续的n个1.

若前两次的结果为 10, 那么剩下的任务就是恰好使用m-2次投掷得到到连续的n个1.

若前三次的结果为 110, 那么剩下的任务就是恰好使用m-3次投掷得到到连续的n个1.

若前四次的结果为 1110, 那么剩下的任务就是恰好使用m-4次投掷得到到连续的n个1.

…

若前n-1次的结果为 1…10(n-2个1), 那么剩下的任务就是恰好使用1次投掷得到到连续的n个1.

你或许已经看出来了，这里实际上是在枚举首次出现0的位置。由于首个0出现在位置i的概率为1/2^i，于是得到Pnm的递推公式

　　

于是根据初始条件：，，我们可以推出所有事件的概率。现在来推一下概率生成函数，设需要得到连续n个1的投掷数的概率生成函数为Gn(z)，于是有

　　

根据上面的递推公式和初始条件，可以得到

　　

于是可解得

　　

分别代入 n = 1 和 n = 2 可以得到

　　

　　

以我们前面得到的结果一致，这证明这个概率生成函数的确是正确的。有了生成函数后，我们又多了一种计算期望的方式

　　

而方差也可以非常容易的得到

　　

至此，这个抛硬币的问题终于应该算是被完全解决了，完。

 ————————————————————————————————————————————————

题目： 一个骰子，6面，1个面是 1， 2个面是2， 3个面是3， 问平均掷多少次能使1、2、3都至少出现一次。

方法： 面对面试概率题几乎屡试不爽的分叉树递归列方程法。

这是一个求数学期望的问题，最终是求1，2，3出现至少一次的最短长度的期望。

这样分叉树的每个节点是一个期望状态，而每个分叉是一次投掷结果。将后续期望出现1、2、3各至少一次的情形记作L123（即题目所求），将后续期望出现1、2各至少一次（3无关）情形记作L12，而1至少一次（2，3无关）情形L1，其余数值符号类推，则树结构如下（列出4级结构已经足够）：

第一级（树根） 第二级 第三级 第四级别
L123 掷1->L23 掷1->L23 同状态
    掷2->L3 根据投掷结果，或继续期待L3，或已经达到目标
    掷3->L2 根据投掷结果，或继续期待L2，或已经达到目标
  掷2->L13 掷1->L3 根据投掷结果，或继续期待L3，或已经达到目标
    掷2->L13 同状态
    掷3->L1 根据投掷结果，或继续期待L1，或已经达到目标
  掷3->L12 掷1->L2 根据投掷结果，或继续期待L2，或已经达到目标
    掷2->L1 根据投掷结果，或继续期待L1，或已经达到目标
    掷3->L12 同状态

接下来，就是要排出方程，因为一共7个未知数，如果排出7个线性方程就能解决问题。

这方程组里的未知数对应上述的状态，而其数值则是一个对长度（投掷次数）的数学期望。

根据这个树状结构和其中的递归关系，这个方程组就是：

L123 = p1 (L23+ 1) + p2 (L13+1) + p3 (L12 + 1) = p1 L23 +p2 L13+ p3 L12 + 1

（以这个L123为例，解释，投掷1的概率是p1而由此得到的结果是需要期待后续2和3各至少出现一次，于是长度期望是L23+ 1，加1是因为投掷了一次，亦即即增进一级）

L23 = p1 L23 +p2 L3+ p3 L2 + 1

L13 = p1 L3 +p2 L13+ p3 L1 + 1

L12 = p1 L2 +p2 L1+ p3 L12 + 1

L1 =p1 + p2 L1+ p3 L1 + 1

（这里实际上是 L1 =p1 ·1 + p2 (L1+1) + p3 (L1 +1) =p2 L1+ p3 L1 + 1，因为对L1情形，如果投了1就目的达到终止了）

L2 =p2 + p1 L2 +  p3 L2 + 1

L3 =p3 + p1 L3 +p2 L3+ 1

（以上一开始没注意，多加了悬空的概率项，故计算有误）

其中 p1，p2 和 p3分别是掷出1，2和3的概率，即1/6，1/3，1/2。

于是求解这个方程，得到：

L1 = 6， L2 = 3， L3 = 2

L12 = 7， L13 = 13/2， L23 = 19/56

L123 = 219/30 = 7.3 259/36 ~= 7.14

故以上如果没有计算错误，该题结果是，平均掷7.3 约7.14次可出现这些面值各至少一次。

 

 ——————————————————————————————————————————————

（转自：http://www.cnblogs.com/atyuwen/archive/2010/09/12/coin.html）

问题：

一个骰子，6面，1个面是 1， 2个面是2， 3个面是3， 问平均掷多少次能使1,2,3都至少出现一次？

一共有三种方法可以解此问题：概率公式、分叉树递归列方程法、指示器变量法。

1. 方法一：概率公式

化为概率的表示是：

1发生 的概率是1/6,  2发生的概率是2/6,  3发生的概率是3/6，求1,2,3至少出现一次的投掷次数的期望。

思路：

第一二次肯定不可能出现这种情况
第x(x > 2)次三个都出现的情况分三种（x ^ y 表示 x 的 y 次方）

1：第x次出现 1，那么前面出现的必然是 2 和 3 ，且至少出现一次   
   出现1的概率为 1 / 6，前面x-1次不出现1的概率为(1 - 1 / 6) ^ (x - 1)，但是其中包含全是 2 和全是 3 的情况，去掉全 2 的概率 (1 / 2) ^ (x - 1)，全部为3的概率(1 / 3) ^ (x - 1)，那么情况 1 的概率为 ((1 - 1 / 6) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1)) * (1 / 6)

2：第x次出现2，那么前面出现的必然是 1 和 3 ，且至少出现一次
   同样，概率为 ((1 - 1 / 3) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 3)

3：第x次出现3，那么前面出现的必然是 1 和 2 ，且至少出现一次
   同样，概率为 ((1 - 1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 2)

p(x)就为上面三种情况的和

那么，根据期望公式，平均值就等于从x = 3 到 n（无穷）求(x * p(x))的和

利用错位相减法计算极限值

 

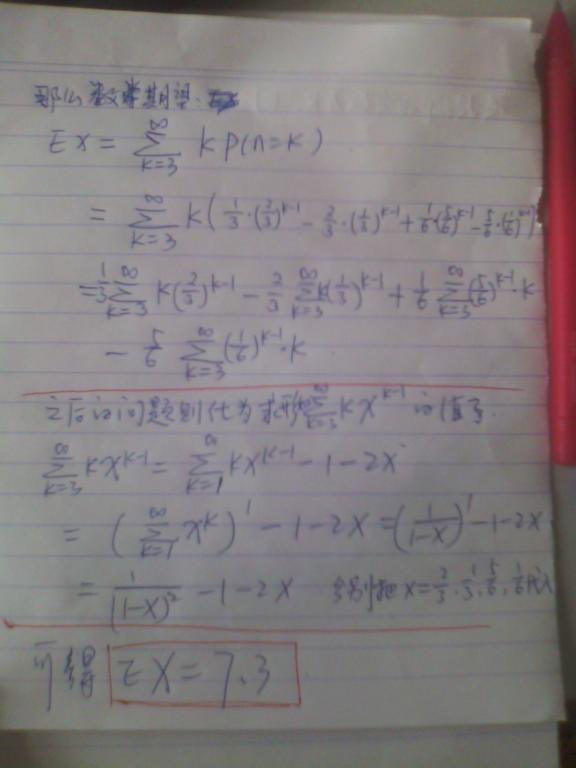
到此可以算出期望为7.3。

2. 方法二：分叉树递归列方程法

 

方法： 面对面试概率题几乎屡试不爽的分叉树递归列方程法。

这是一个求数学期望的问题，最终是求1，2，3出现至少一次的最短长度的期望。

这样分叉树的每个节点是一个期望状态，而每个分叉是一次投掷结果。将后续期望出现1、2、3各至少一次的情形记作L123（即题目所求），将后续期望出现1、2各至少一次（3无关）情形记作L12，而1至少一次（2，3无关）情形L1，其余数值符号类推，则树结构如下（列出4级结构已经足够）：

 

第一级（树根） 第二级 第三级 第四级别
L123 掷1->L23 掷1->L23 同状态
    掷2->L3 根据投掷结果，或继续期待L3，或已经达到目标
    掷3->L2 根据投掷结果，或继续期待L2，或已经达到目标
  掷2->L13 掷1->L3 根据投掷结果，或继续期待L3，或已经达到目标
    掷2->L13 同状态
    掷3->L1 根据投掷结果，或继续期待L1，或已经达到目标
  掷3->L12 掷1->L2 根据投掷结果，或继续期待L2，或已经达到目标
    掷2->L1 根据投掷结果，或继续期待L1，或已经达到目标
    掷3->L12 同状态

 

 

接下来，就是要排出方程，因为一共7个未知数，如果排出7个线性方程就能解决问题。

这方程组里的未知数对应上述的状态，而其数值则是一个对长度（投掷次数）的数学期望。

根据这个树状结构和其中的递归关系，这个方程组就是：

L123 = p1 (L23+ 1) + p2 (L13+1) + p3 (L12 + 1) = p1 L23 +p2 L13+ p3 L12 + 1

（以这个L123为例，解释，投掷1的概率是p1而由此得到的结果是需要期待后续2和3各至少出现一次，于是长度期望是L23+ 1，加1是因为投掷了一次，亦即即增进一级）

L23 = p1 L23 +p2 L3+ p3 L2 + 1

L13 = p1 L3 +p2 L13+ p3 L1 + 1

L12 = p1 L2 +p2 L1+ p3 L12 + 1

L1 =p2 L1+ p3 L1 + 1

（这里实际上是 L1 =p1 ·1 + p2 (L1+1) + p3 (L1 +1) =p2 L1+ p3 L1 + 1，因为对L1情形，如果投了1就目的达到终止了）

L2 = p1 L2 + p3 L2 + 1

L3 = p1 L3 +p2 L3+ 1

其中p1，p2和p3分别是掷出1，2和3的概率，即1/6，1/3，1/2。

于是求解这个方程，得到：

L1 = 6， L2 = 3， L3 = 2

L12 = 7， L13 = 13/2， L23 = 19/5

L123 = 219/30 = 7.3 

平均掷7.3 次可出现这些面值各至少一次。

3. 方法三：指示器变量法

【另一解法】感谢4楼aaaxingruiaaa同学提供的答案（指示器变量法），整理如下：

定义随机变量Xn，其可能值为0或1，其值为1表示“前n次掷骰子，1，2，3没能都至少出现一次”的事件，其值为0表示这个事件没有发生，即“前n次掷骰子，1，2，3各至少出现一次”。

令pn为“掷n次骰子，1，2，3没能都至少出现一次”的概率，所以显然pn = Pr{Xn=1}，于是pn = 1·Pr{Xn=1} + 0·Pr{Xn=1} = E[Xn]，即这个随机变量的数学期望。

令随机变量X表示1，2，3刚好全部出现过需要的投掷次数。可见题目要求的就是E[X]。

关键等式：X = Sigma(n=0 to Inf; Xn) （这里Sigma是求和号，求和范围是n从0到无穷大）

说明一下，等式两边都是随机变量，假设对于某个随机实例（例如，这里指一次具体的投掷序列），其对应事件是：“投了K次恰好1，2，3都出现了”，于是等式左边显然等于K；而等式右边，对于n < K，由于这些项的对应定义事件发生了（即1，2，3没能出现），所以他们的实例值是1，而对于n⩾K，则由于对应定义事件都没发生，实例值为0，可见这个和也是K。故两侧相等。（为了达到这个相等关系，可以看出需要把X0包含在内的必要性）

值得注意的是（但对于解这道题也可以不去注意，但注意一下有利于比较深入地理解），对n < 3，Xn显然恒为1。而对于n⩾3，这些随机变量不是独立的。他们的相关性是不容易求出的，唯一容易知道的是，当序列中一个项为0时，其后的项均为0。好在对于这题我们不需要担忧这个相关性。

由于数学期望的加性与随机变量的相关性无关（这是数学期望一个很令人高兴的性质），所以即便这样，E[X]也能容易求出：

E[X] = Sigma(n=0 to Inf; E[Xn]) = Sigma(n=0 to Inf; pn)

pn的比较直观的求法也由aaaxingruiaaa同学提供了，即所谓容斥原理。稍微解释一下，由于pn考虑的是n次投掷三者没有全部出现，于是就是其中两者出现或仅一者出现。假设单次投掷1，2和3出现的概率分别为：r1，r2和r3。于是(r1+r2)n表征n次投掷只出现1或2的概率，这其中包括了出现全1和全2的情形，于是求pn可由这样的项求和并剔除重复计算的单面值情形，于是：

pn = (r1+r2)n+ (r1+r3)n+ (r2+r3)n-r1n-r2n-r3n，当n > 0； 而p0 = 1 （由定义；同时也可以检验看出，这个pn在n为1和2的时候都是1）

于是由等比级数（等比数列求和）公式：

E[X] = 1 + Sigma(n=1 to Inf; (r1+r2)n+ (r1+r3)n+ (r2+r3)n-r1n-r2n-r3n= 1 + (1 - r3) / r3 + (1 - r2) / r2 + (1 - r1) / r1- r1 / (1 - r1) - r2 / (1 -r2) -r3 / (1 - r3) = 7.3

http://blog.csdn.net/quanben/article/details/6918209

 

假设有一个硬币，抛出字（背面）和花（正面）的概率都是0.5，而且每次抛硬币与前次结果无关。现在做一个游戏，连续地抛这个硬币，直到连续出现两次字为止，问平均要抛多少次才能结束游戏？注意，一旦连续抛出两个“字”向上游戏就结束了，不用继续抛。
上面这个题目我第一次见到是在pongba的TopLanguage的一次讨论上，提出问题的人为Shuo Chen，当时我给出了一个解法，自认为已经相当简单了，先来考虑一下抛硬币的过程：首先先抛一枚硬币，如果是花，那么需要重头开始；如果是字，那么再抛一枚硬币，新抛的这枚如果也是字，则游戏结束，如果是花，那么又需要重头开始。根据这个过程，设抛硬币的期望次数为T，可以得到关系：
　　T = 1 + 0.5T + 0.5( 1 + 0.5 * 0 + 0.5T) 
解方程可得到 T = 6。

或者根据公式，需要连续抛出n个字的一般情形，结果相当简洁：Tn = 2^(n+1) - 2，其中Tn为首次出现连续的n个字的期望投掷数。

公式证明如下：

方法一：

设出现连续k次正面的期望是a[k]
则出现连续k+1次正面的期望为a[k+1]
在出现连续k次正面后，有下面几种情况：
i)下一个是正面，概率1/2，总次数a[k]+1;
ii)下一个是反面，概率1/2，则接下来平均仍需a[k+1],总次数a[k]+1+a[k+1]。
因此a[k+1]=(a[k]+1)/2+(a[k]+1+a[k+1])/2
整理得(a[k+1]+2)/(a[k]+2)=2
a[n]=(a[1]+2)*2^(n-1)-2
显然a[1]=2;a[n]=2^(n+1)-2

方法二：

转自matrix67  http://www.matrix67.com/blog/archives/3638

 

设想有这么一家赌场，赌场里只有一个游戏：猜正反。游戏规则很简单，玩家下注 x 元钱，赌正面或者反面；然后庄家抛出硬币，如果玩家猜错了他就会输掉这 x 元，如果玩家猜对了他将得到 2x 元的回报（也就是净赚 x 元）。
让我们假设每一回合开始之前，都会有一个新的玩家加入游戏，与仍然在场的玩家们一同赌博。每个玩家最初都只有 1 元钱，并且他们的策略也都是相同的：每回都把当前身上的所有钱都押在正面上。运气好的话，从加入游戏开始，庄家抛掷出来的硬币一直是正面，这个玩家就会一直赢钱；如果连续 n 次硬币都是正面朝上，他将会赢得 2^n 元钱。这个 2^n 就是赌场老板的心理承受极限——一旦有人赢到了 2^n 元钱，赌场老板便会下令停止游戏，关闭赌场。让我们来看看，在这场游戏中存在哪些有趣的结论。

首先，连续 n 次正面朝上的概率虽然很小，但确实是有可能发生的，因此总有一个时候赌场将被关闭。赌场关闭之时，唯一赚到钱的人就是赌场关闭前最后进来的那 n 个人。每个人都只花费了 1 元钱，但他们却赢得了不同数量的钱。其中，最后进来的人赢回了 2 元，倒数第二进来的人赢回了 4 元，倒数第 n 进来的人则赢得了 2^n 元（他就是赌场关闭的原因），他们一共赚取了 2 + 4 + 8 + … + 2^n = 2^(n+1) - 2 元。其余所有人初始时的 1 元钱都打了水漂，因为没有人挺过了倒数第 n + 1 轮游戏。
另外，由于这个游戏是一个完全公平的游戏，因此赌场的盈亏应该是平衡的。换句话说，有多少钱流出了赌场，就该有多少的钱流进赌场。既然赌场的钱最终被赢走了 2^(n+1) - 2 元，因此赌场的期望收入也就是 2^(n+1) - 2 元。而赌场收入的唯一来源是每人 1 元的初始赌金，这就表明游戏者的期望数量是 2^(n+1) - 2 个。换句话说，游戏平均进行了 2^(n+1) - 2 次。再换句话说，平均抛掷 2^(n+1) - 2 次硬币才会出现 n 连正的情况。

——————————————————————————————————————————————————————

转自 http://www.cnblogs.com/aquastone/archive/2012/10/19/Prob_CoinContinuousNPositive.html

1. 问题描述

连续抛一枚硬币，连续出现若干次正面即停止，求所抛总次数的期望。

2. 求解期望

记硬币出现正面的概率为p，停止条件中连续出现正面的次数为n，所抛总次数的期望为μn。考虑如下情形：首次出现连续n−1次正面，此时所抛总次数的期望为μn−1。再抛一次，结果有且只有一下两种：

  • A. 出现正面，则满足停止条件，所抛总次数的期望为μn−1+1
  • B. 出现反面，则立即回到初始状态，相当于从0开始再抛出n次连续正面，因此总次数的期望为μn−1+1+μn。A、B两种情况的概率分别为p,1−p。因此有

 

μn=p(μn−1+1)+(1−p)(μn−1+1+μn)(1)

 

得

 

μn=1p(μn−1+1)(2)

 

展开，得通项公式

 

(3)

 

 

μn=s(1−sn)1−s,s=1p(4)

 

特别的，对于一枚均匀硬币，p=1/2，因此μn=2n+1−2。

3. 概率计算

进一步考虑该问题，尝试求解连续抛出n次正面时，所抛总次数为m的概率P(n,m)。显然，

 

P(n,m)=0m<nP(0,m)={10m=0m≥1

 

依然考虑第2节中的两种情况。

  • 对于A，在首次连续出现n−1次正面的情况下，再抛一次出现正面，满足停止条件，因此需要前面总共抛了m−1次，这一概率为P(n−1,m−1)。
  • 对于B，设首次连续出现n−1次正面时，已经抛了k次，再抛一次出现反面，立即回到初始状态，因此，要满足总次数为m，需要在后续的步骤里，恰好用m−k−1次抛出n次连续正面。因此B情况下的条件概率为∑kP(n−1,k)P(n,m−k−1)。

由全概率公式，得

 

P(n,m)=pP(n−1,m−1)+(1−p)∑kP(n−1,k)P(n,m−k−1)(5)

 

实际上，可以由P(n,m)的递推式(5)得出μn的递推式(2)。依据期望的定义

 

μn=∑mmP(n,m)=p∑mmP(n−1,m−1)+(1−p)∑m∑kmP(n−1,k)P(n,m−k−1)

 

第一项中的求和式可以写成

 

∑m−1(m−1+1)P(n−1,m−1)=∑m−1(m−1)P(n−1,m−1)+∑m−1P(n−1,m−1)=μn−1+1

 

第二项中的求和式可以写成

 

∑m∑k(k+1+m−k−1)P(n−1,k)P(n,m−k−1)=∑kkP(n−1,k)∑mP(n,m−k−1)+∑kP(n−1,k)∑mP(n,m−k−1)+∑k∑m(m−k−1)P(n−1,k)P(n,m−k−1)=μn−1+1+μn

 

可证。

4. 数值结果

根据P(n,m)的递推式(5)，写出对应的Matlab程序如下。

复制代码
N = 6;    % numbers of continuous positive in stop conditions
M = 3000; % total times when stop condition satisfied
p = 1/2;  % probability of positive

% Initial Conditions. P is a matrix in size of N+1,M+1 and the element 
% with index n+1,m+1 stands for P(n,m) because there are no index 0.
P = zeros(N+1,M+1);
P(1,1) = 1;
% Iteration
for nn = 1:N
    for mm = 1:M
        tmp = 0;
        for kk = nn-1:mm-nn-1
             tmp = tmp + P(nn-1+1,kk+1)*P(nn+1,mm-kk-1+1);
        end
        P(nn+1,mm+1) = P(nn-1+1,mm-1+1)*p + tmp*(1-p);
    end
end
P=P(2:end,2:end)';  % get rid of P(0,m) & P(n,0)
semilogy(P); % no plot of P(0,m)
disp(['Check the sum of probability:']);
disp(sum(P));
disp(['Compute the expectation of total times:']);
disp((1:M)*P);
复制代码

 为了产生直观的印象，对p=1/2的情况计算前面几项的结果。计算N=3,M=16，作出P(n,m)的半对数图如下。

 

为了验证∑mP(n,m)=1，以及根据此概率求期望∑mmP(n,m)，将N,M增大至6,5000。程序输出为

Check the sum of probability:
    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000

Compute the expectation of total times:
    2.0000    6.0000   14.0000   30.0000   62.0000  126.0000

显然，验证了概率之和为1。另外，容易验证所求出的期望与μn的通项公式(4)给出的结果是一致的。

5. 模拟验证

使用Mote Carlo模拟的方法对这一问题进行仿真，代码如下

复制代码
len = 2e8;   % length of random numbers
N = (1:6)';  % numbers of continuous positive in stop conditions

for pp = 1:length(N)
    res = rand(len,1)>0.5;    % uniform distribution, >0.5 stands for positive
    
    currTotalTime = 0; % total times when stop condition satisfied
    contPosCntr = 0;   % continuous positive appears
    numExper = 0;
    totalTimeRcd = nan(len,1);
    for ii = 1:len
        currTotalTime = currTotalTime+1;
        if (res(ii))
            contPosCntr = contPosCntr+1;
        else
            contPosCntr = 0;
        end

        if (contPosCntr>=N(pp))
            numExper = numExper+1;
            totalTimeRcd(numExper) = currTotalTime;
            contPosCntr = 0;
            currTotalTime = 0;
        end
    end

    meanT = mean(totalTimeRcd(1:numExper));
end
复制代码

结果如下：

N=1: 2.000015
N=2: 6.000249
N=3: 14.001627
N=4: 29.985933
N=5: 62.000438
N=6: 126.052749

与理论结果一致。

6. 附注

该问题还有其他表现形式，如：

  • 有一个通关游戏，设每关所需的时间固定为1，而通关概率为p。如果某关失败，则必须重新从第一关打起。问通关的平均时间。

这类问题本质上是一致的，都可以归结为在一系列连续实验中，首次连续出现n次成功的平均时间。

posted @ 2013-06-28 20:28  Avril  阅读(25822)  评论(0)  编辑  收藏  举报