CF1368G Shifting Dominoes
Shifting Dominoes
Bill likes to play with dominoes. He took an \(n \times m\) board divided into equal square cells, and covered it with dominoes. Each domino covers two adjacent cells of the board either horizontally or vertically, and each cell is covered exactly once with a half of one domino (that is, there are no uncovered cells, and no two dominoes cover the same cell twice).
After that Bill decided to play with the covered board and share some photos of it on social media. First, he removes exactly one domino from the board, freeing two of the cells. Next, he moves dominoes around. A domino can only be moved along the line parallel to its longer side. A move in the chosen direction is possible if the next cell in this direction is currently free. Bill doesn't want to lose track of what the original tiling looks like, so he makes sure that at any point each domino shares at least one cell with its original position.
After removing a domino and making several (possibly, zero) moves Bill takes a photo of the board and posts it. However, with the amount of filters Bill is using, domino borders are not visible, so only the two free cells of the board can be identified. When the photo is posted, Bill reverts the board to its original state and starts the process again.
Bill wants to post as many photos as possible, but he will not post any photo twice. How many distinct photos can he take? Recall that photos are different if the pairs of free cells in the photos are different.
\(nm \leq 2 \cdot 10^5\)
题解
Let's think of how a certain cell can be freed up. One way is to just lift the domino covering it from the start. If we didn't do it, then we must move the domino covering the cell, and there is exactly one way of doing so. But at this point the cell we've moved to should have been free. We can follow this chain of events, and we must eventually arrive to a cell that was covered by the initially removed domino.
This is more readily seen if we draw a graph with vertices being cells, and edges leading from the cell freed up by moving a domino to the cell becoming occupied by doing so. Note that some of the cells are impossible to free up with such a move.
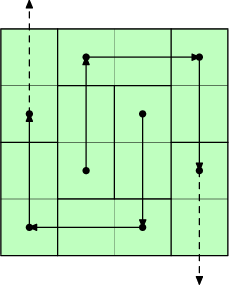
Let us study this graph a bit more. If we color the board like a chessboard, we can see that edges always connect cells of the same color, so the two subgraphs for white and black cells are independent. Further, since initially a white and a black cell are freed, the two free cells will always have different colors.
In this graph each vertex (= cell) has out-degree at most \(1\). In general directed graphs of this kind are called functional graphs, and look like a bunch of trees linked to directed cycles. However, it turns out that our graph can not have cycles! To prove this, let's look a how this cycle would look like:
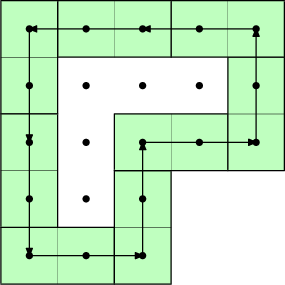
Centers of all the cells in a cycle form a lattice polygon. The area of such a polygon can be found with Pick's formula: \(S = I + B / 2 - 1\), where \(I\) and \(B\) is the number of lattice points inside and on the boundary respectively. However, we can observe that:
-
\(B\) is the length of the boundary. The boundary can be broken into segments of length \(2\). The length of upward and downward arrows is the same, therefore the length of vertical borders is divisible by \(4\), same for horizontal arrows. Thus \(B\) is divisible by \(4\), and \(B / 2\) must be even.
拐角处只需要把相邻两个拐角点一个分给横着的一个分给竖着的就行了。
-
Inside of the polygon can be broken down into \(2 \times 2\) squares, therefore \(S\) must be even.
注意这里的内部不是那些无色格子。
-
\(I = S - B / 2 + 1\) should therefore be odd. However, the inside of the cycle is isolated from the outside, and therefore should be independently tilable with dominoes. But the number of cells (= vertices) inside the cycle is odd, therefore it's impossible.
Since our directed graph has no cycles, it must be a directed forest, which makes it much easier to handle.
Now consider a pair of cells \(c_1, c_2\) of different colors, and look at the paths \(P_1\) and \(P_2\) starting at these cells. If these paths reach the boundary without visiting the same domino, then the pair \(c_1, c_2\) is impossible to free up, since we would have to remove at least two dominoes.
If the paths do visit at least one common domino, then we argue that the pair is possible to free up. Indeed, consider the first domino \(D\) on \(P_1\) that is also visited by \(P_2\). If we remove \(D\), then the parts of \(P_1\) and \(P_2\) until \(D\) can not intersect, thus it is possible to move dominoes to free \(c_1\) and \(c_2\) without trying to move any domino twice.
To figure out the answer, consider the two forests \(F_1\) and \(F_2\) built up by black and white cells of the board. If we label each cell of each forest with the index of the domino covering this cell, then the answer is equal to the number of pairs of cells \(c_1 \in F_1\), \(c_2 \in F_2\) such that the paths starting at \(c_1\) and \(c_2\) have common labels. To actually compute the answer we will instead count the cell pairs with label-disjoint paths.
This is now a fairly standard data structure problem. Construct Euler tours in both \(F_1\) and \(F_2\). Then, the subtree of each vertex is a segment in the Euler tour. For a cell \(c_1 \in F_1\) labeled with domino \(D\), suitable cells in \(F_2\) are the ones not in the subtree of a cell sharing the label with \(c_1\) or with any parent of \(c_1\).
Euler tours也就是DFS序。
Perform a DFS of \(F_1\), following edges in reverse. When we enter a cell labeled \(D\), locate the cell with this label in \(F_2\) and mark all vertices in its subtree. At this point, we should add the number of unmarked cells in \(F_2\) to the answer. When we leave the cell, revert to the previous configuration before marking the subtree. Implementation-wise, this can be done with a segment tree that supports adding on a segment (= subtree in the Euler tour), and finding the number of zeros (= unmarked cells).
其实没必要算反面。线段覆盖的总长度是扫描线经典问题。
Segment tree is the most demanding component of the solution, thus the complexity is \(O(nm \log (nm))\).
CO int N=2e5+10;
int tree[4*N],tag[4*N];
#define lc (x<<1)
#define rc (x<<1|1)
#define mid ((l+r)>>1)
void modify(int x,int l,int r,int ql,int qr,int v){
if(ql<=l and r<=qr){
tag[x]+=v;
tree[x]=tag[x]?r-l+1:tree[lc]+tree[rc];
return;
}
if(ql<=mid) modify(lc,l,mid,ql,qr,v);
if(qr>mid) modify(rc,mid+1,r,ql,qr,v);
tree[x]=tag[x]?r-l+1:tree[lc]+tree[rc];
}
#undef lc
#undef rc
#undef mid
char getUDLR(){
char c=getchar();
while(c!='U' and c!='D' and c!='L' and c!='R') c=getchar();
return c;
}
vector<int> cell[N],point[N];
vector<int> toa[N],tob[N];
bool visa[N],visb[N];
int pos[N],lst[N],tim;
void dfsa(int x){
pos[x]=++tim;
for(int y:toa[x]) dfsa(y);
lst[x]=tim;
}
int64 dfsb(int x){
modify(1,1,tim,pos[x],lst[x],1);
int64 ans=tree[1];
for(int y:tob[x]) ans+=dfsb(y);
modify(1,1,tim,pos[x],lst[x],-1);
return ans;
}
int main(){
int n=read<int>(),m=read<int>();
for(int i=0;i<=n+1;++i){
cell[i].resize(m+2);
point[i].resize(m+2);
}
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)
cell[i][j]=getUDLR();
int num=0;
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j){
if(cell[i][j]=='D') point[i][j]=point[i-1][j];
else if(cell[i][j]=='R') point[i][j]=point[i][j-1];
else point[i][j]=++num;
}
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j){
int x=0;
if(cell[i][j]=='U') x=point[i+2][j];
else if(cell[i][j]=='D') x=point[i-2][j];
else if(cell[i][j]=='L') x=point[i][j+2];
else x=point[i][j-2];
if(!x) continue;
if((i+j)%2==0) toa[x].push_back(point[i][j]),visa[point[i][j]]=1;
else tob[x].push_back(point[i][j]),visb[point[i][j]]=1;
}
for(int i=1;i<=num;++i)if(!visa[i]) dfsa(i);
int64 ans=0;
for(int i=1;i<=num;++i)if(!visb[i]) ans+=dfsb(i);
printf("%lld\n",ans);
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号