SNOI2020 生成树

生成树

给定无向连通图 \(G\)，已知 \(G\) 在删掉一条边后是一颗仙人掌（仙人掌：不存在两个拥有公共边的简单环的无向联通图），求 \(G\) 的生成树个数。结果对 \(998244353\) 取模。

对于所有数据，\(1\le n\le m\le 5\times 10^5\)。

题解

https://blog.csdn.net/C20181220_xiang_m_y/article/details/107006724

如果就是原图是仙人掌那么答案显然是所有环大小之积。

\(G\)删掉一条边后是仙人掌，那么\(G\)一定是这样的形式：

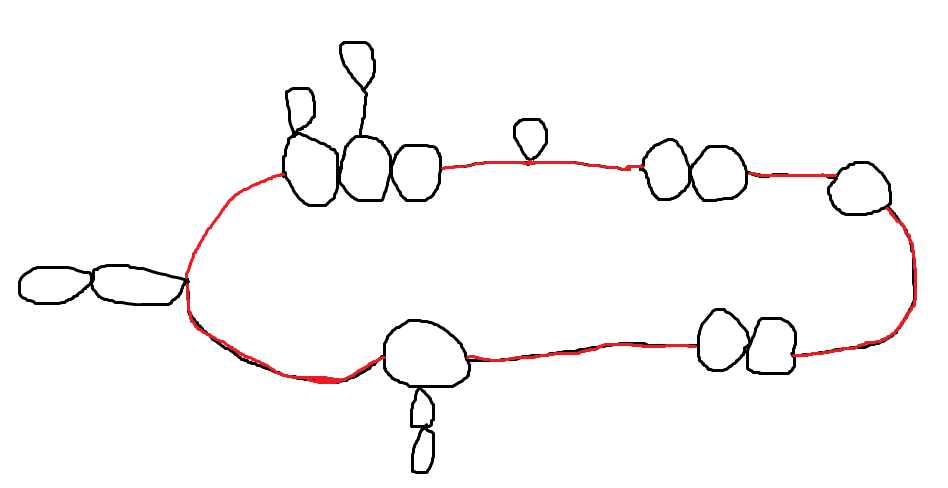
就是一个大环串起了一些仙人掌串，没有被大环串起的对答案的贡献就是乘上环大小。而且其中必然存在至少一条不在小环中的边（只有两个环贴在一起的情况特殊考虑，实现相同），就是上图中的红色边，记这样的边的条数为\(cnt\)，记小环的大小为\(siz_i\)，小环两半边大小分别为\(l_i,r_i\)，那么形成生成树要么是断一条红边，所有环断一条边，要么是断两条不在同一半的环边，其它环断一条边。答案为

\[cnt*(\prod siz_i)+(\sum {l_i*r_i\over siz_i})*(\prod siz_i) \]

那么问题就是要求出\(cnt\)和\(siz_i\)以及每个环某一半的大小。

先tarjan一遍求出这个大环对应的点双，将其拿出来建新图（除去不相关的点和边），这个大环一定满足 边数 > 点数，tarjan求点双的边数可以通过在栈中加入边解决。

然后断开一条红色边，使其形成一个仙人掌，观察可以发现度数为3的点一定有一条是红色边，所以枚举某个度数为3的点的所有边断开检验是否是仙人掌即可。

在得到仙人掌的过程中就可以记录得到的点双大小，某一半的大小可以通过记录dfs深度相减得到，因为环上只有进入和出去的点的度数>2，可以借此求解。

时间复杂度\(O(n)\)。

CO int N=5e5+10;
int inv[N];
pair<int,int> edge[N];
int head[N],to[2*N],nxt[2*N],tot=1;

IN void link(int x,int y){
	nxt[++tot]=head[x],head[x]=tot,to[tot]=y;
}

int pos[N],low[N],tim,stk[2*N],top;
int dep[N],deg[N],dis[N],num;
vector<int> scc[N],big;
int id,ban[N],onc[N];

void tarjan(int x,int fa){
	pos[x]=low[x]=++tim,stk[++top]=x;
	for(int i=head[x];i;i=nxt[i])if(!ban[i/2] and i!=(fa^1)){
		int y=to[i];
		if(!pos[y]){
			stk[++top]=-i,dep[y]=dep[x]+1;
			tarjan(y,i);
			low[x]=min(low[x],low[y]);
			if(low[y]==pos[x]){
				scc[++num]={x};
				int e=0;
				for(int t=0;t!=-i;){
					t=stk[top--];
					if(t<0) ++e;
					else{
						scc[num].push_back(t);
						if(deg[t]>2) dis[num]=dep[t]-dep[x];
					}
				}
				if(e>(int)scc[num].size()) id=num;
			}
			else if(low[y]>pos[x]) top-=2; // -i and y
		}
		else if(pos[y]<pos[x])
			stk[++top]=-i,low[x]=min(low[x],pos[y]);
	}
}

int main(){
	int n=read<int>(),m=read<int>();
	inv[0]=inv[1]=1;
	for(int i=2;i<=n;++i) inv[i]=mul(mod-mod/i,inv[mod%i]);
	for(int i=1;i<=m;++i){
		int x=read<int>(),y=read<int>();
		edge[i]={x,y},link(x,y),link(y,x);
	}
	tarjan(1,0);
	int prod=1;
	for(int i=1;i<=num;++i)if(i!=id) prod=mul(prod,scc[i].size());
	if(!id){
		printf("%d\n",prod);
		return 0;
	}
	big=scc[id];
	fill(head+1,head+n+1,0),tot=1;
	for(int x:big) onc[x]=1;
	int all=0;
	for(int i=1;i<=m;++i){
		int x=edge[i].first,y=edge[i].second;
		if(onc[x] and onc[y])
			++all,++deg[x],++deg[y],link(x,y),link(y,x);
	}
	for(int x:big)if(deg[x]==3){
		for(int i=head[x];i;i=nxt[i]){
			ban[i/2]=1;
			fill(pos+1,pos+n+1,0),dep[x]=0,top=tim=num=id=0;
			tarjan(x,0);
			if(id) {ban[i/2]=0; continue;}
			int cnt=0,pwr=1,sum=0;
			for(int j=1;j<=num;++j){
				pwr=mul(pwr,scc[j].size()),cnt+=scc[j].size();
				sum=add(sum,mul(dis[j],mul(scc[j].size()-dis[j],inv[scc[j].size()])));
			}
			printf("%d\n",mul(sum+all-cnt,mul(pwr,prod)));
			return 0;
		}
	}
	return 0;
}