HDU6585 Desert

Desert

Tom and Jerry got lost in a desert. But they are not bored or afraid at all, because they found a truly interesting thing to do: researching the varied kinds of kakti in the desert!

After careful observations, they found that a kaktus can be seen as a graph consisting of several nodes. To be precise, an \(n\)-node kaktus is an undirected connected graph that has only \(1\) node as the root, in which every edge belongs to exactly one simple cycle and all nodes are unlabelled. You can refer to sample case for a better understanding.

Finding something new is always exciting, but it brings them new doubts.

"How many different kinds of \(n\)-node kakti are there?" wondered Tom.

"Your problem is simpler than mine. I am wondering how many different kinds of \(1,2,3,..,n\)-node kakti there are." said Jerry.

\(n \leq 10^5\)。

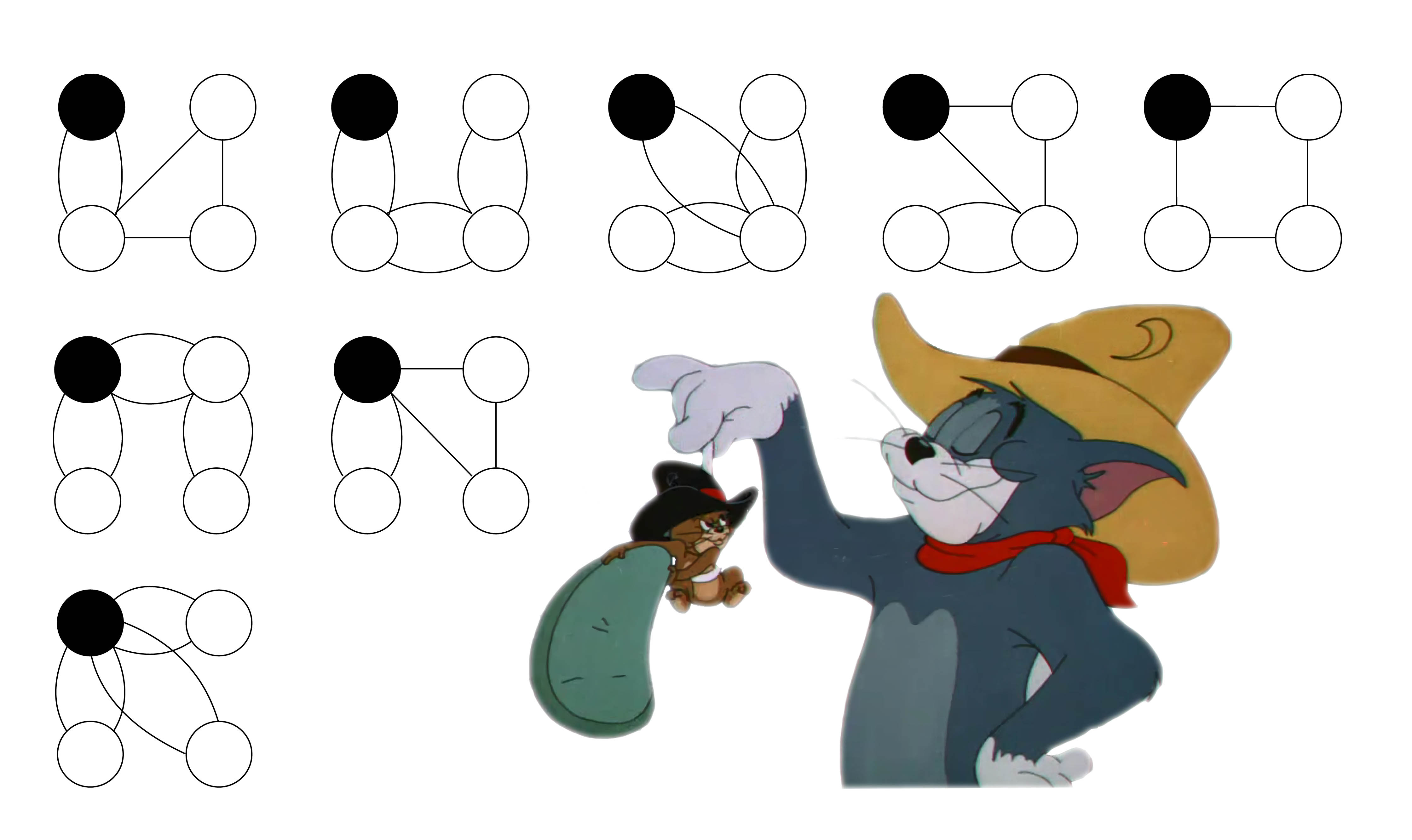
题解

题目中要求每条边都必须恰好在一个环中，样例解释的图给出了重边的情况。我们可以认为重边就是普通仙人掌的单边，那么问题就转化成了无标号有根仙人掌计数。

记 \(F(x)\) 为无标号有根仙人掌的生成函数。用有标号有根仙人掌计数和无标号有根树计数的老套路，先枚举根，然后再用欧拉变换。

枚举环的时候使用Burnside引理。由于根已经固定，所以环不能旋转，只能对称。所以我们就枚举不变和对称两种置换暴力计算。

\[F(x)=x\mathcal{E}\left(F(x)+\sum_{i=2}^\infty \frac{F(x^2)^{\lfloor i/2 \rfloor}F(x)^{i\bmod 2}+F(x)^i}{2}\right) \]

记括号里的式子

\[Q(x)=F(x)+\sum_{i=2}^\infty \frac{F(x^2)^{\lfloor i/2 \rfloor}F(x)^{i\bmod 2}+F(x)^i}{2}\\ =F(x)+\frac{1}{2}\sum_{i=2}^\infty F(x)^i+\frac{1}{2}(F(x)+1)\sum_{i=1}^\infty F(x^2)^i\\ \frac{1}{2}\sum_{i=0}^\infty F(x)^i-\frac{1}{2}+\frac{1}{2}(F(x)+1)\sum_{i=0}^\infty F(x^2)^i-\frac{1}{2}\\ =\frac{1}{2}\left(\frac{1}{1-F(x^2)}+\frac{1}{1-F(x)^2}\right)(F(x)+1)-1 \]

直接从最后这个结果入手也可以，意义还是很明显。由这个分数式我们知道，\(Q(x)\) 的常数项为 \(0\)，并且如果把 \(x\) 换成 \(x^k~(k>n)\) 的话，它在 \(\mod x^{n}\) 的意义下应该等于 \(0\)。

记

\[P(x)=\sum_{i=2}^\infty \frac{1}{i}Q(x^i) \]

显然 \(P(x)\) 在 \(\mod x^n\) 是可以看成常数来求导的。根据调和级数，\(P(x)\) 可以在 \(O(n \ln n)\) 的时间内完成计算。

有了这个形式就容易牛顿迭代了。

\[G(F(x))=F(x)-x\exp\left(\sum_{i=1}^\infty \frac{1}{i}Q(x^i)\right)\\ =F(x)-x\exp(P(x)+Q(x))\\ G'(F(x))=1-x\exp(P(x)+Q(x)) Q'(x) \]

通过WolframAlpha我们得到

\[Q'(x)=\frac{1}{2}\left(\frac{1}{1-F(x^2)}+\frac{1}{(-1+F(x))^2}\right) \]

那么所有问题就解决了。回顾牛顿迭代式

\[F(x)=F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))} \]

时间复杂度 \(O(n\log n)\)。

CO int N=262144;
int omg[2][N],rev[N];
int fac[N],inv[N],ifac[N];

void NTT(poly&a,int dir){
    int lim=a.size(),len=log2(lim);
    for(int i=0;i<lim;++i) rev[i]=rev[i>>1]>>1|(i&1)<<(len-1);
    for(int i=0;i<lim;++i)if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=1;i<lim;i<<=1)
        for(int j=0;j<lim;j+=i<<1)for(int k=0;k<i;++k){
            int t=mul(omg[dir][N/(i<<1)*k],a[j+i+k]);
            a[j+i+k]=add(a[j+k],mod-t),a[j+k]=add(a[j+k],t);
        }
    if(dir==1){
        int ilim=fpow(lim,mod-2);
        for(int i=0;i<lim;++i) a[i]=mul(a[i],ilim);
    }
}
poly operator~(poly a){
    int n=a.size();
    poly b={fpow(a[0],mod-2)};
    if(n==1) return b;
    a.resize(1<<(int)ceil(log2(n)));
    for(int lim=2;lim<2*n;lim<<=1){
        poly c(a.begin(),a.begin()+lim);
        c.resize(lim<<1),NTT(c,0);
        b.resize(lim<<1),NTT(b,0);
        for(int i=0;i<lim<<1;++i) b[i]=mul(2+mod-mul(c[i],b[i]),b[i]);
        NTT(b,1),b.resize(lim);
    }
    return b.resize(n),b;
}
poly log(poly a){
    int n=a.size();
    poly b=~a;
    for(int i=0;i<n-1;++i) a[i]=mul(a[i+1],i+1);
    a.resize(n-1);
    int lim=1<<(int)ceil(log2(2*n-2));
    a.resize(lim),NTT(a,0);
    b.resize(lim),NTT(b,0);
    for(int i=0;i<lim;++i) a[i]=mul(a[i],b[i]);
    NTT(a,1),a.resize(n);
    for(int i=n-1;i>=1;--i) a[i]=mul(a[i-1],inv[i]);
    return a[0]=0,a;
}
poly exp(poly a){
    int n=a.size();
    poly b={1}; // a[0]=0
    if(n==1) return b;
    a.resize(1<<(int)ceil(log2(n)));
    for(int lim=2;lim<2*n;lim<<=1){
        b.resize(lim);poly c=log(b);
        c[0]=add(1+a[0],mod-c[0]);
        for(int i=1;i<lim;++i) c[i]=add(a[i],mod-c[i]);
        c.resize(lim<<1),NTT(c,0);
        b.resize(lim<<1),NTT(b,0);
        for(int i=0;i<lim<<1;++i) b[i]=mul(c[i],b[i]);
        NTT(b,1),b.resize(lim);
    }
    return b.resize(n),b;
}
poly operator*(poly a,poly b){
    int n=a.size()+b.size()-1;
    int lim=1<<(int)ceil(log2(n));
    a.resize(lim),NTT(a,0);
    b.resize(lim),NTT(b,0);
    for(int i=0;i<lim;++i) a[i]=mul(a[i],b[i]);
    NTT(a,1),a.resize(n);
    return a;
}

poly calc_F2(CO poly&f){
	int n=f.size();
	poly f2(n);
	for(int i=0;i<n;i+=2) f2[i]=f[i/2];
	return f2;
}
poly calc_Q(poly f,poly f2){
	int n=f.size();
	poly q=f;++q[0];
	f=f*f,f.resize(n);
	f[0]=1+mod-f[0];
	for(int i=1;i<n;++i) f[i]=mod-f[i];
	f2[0]=1+mod-f2[0];
	for(int i=1;i<n;++i) f2[i]=mod-f2[i];
	f=~f,f2=~f2;
	for(int i=0;i<n;++i) f[i]=mul(add(f[i],f2[i]),inv[2]);
	q=f*q,q.resize(n),--q[0];
	return q;
}
poly calc_dQ(poly f,poly f2){
	int n=f.size();
	--f[0],f=f*f,f.resize(n);
	f2[0]=1+mod-f2[0];
	for(int i=1;i<n;++i) f2[i]=mod-f2[i];
	f=~f,f2=~f2;
	for(int i=0;i<n;++i) f[i]=mul(add(f[i],f2[i]),inv[2]);
	return f;
}
poly calc_P(CO poly&q){
	int n=q.size();
	poly p(n);
	for(int i=2;i<n;++i)for(int j=0;j<n;j+=i)
		p[j]=add(p[j],mul(q[j/i],inv[i]));
	return p;
}
poly calc_G(poly f,poly p,poly q){
	int n=f.size();
	for(int i=0;i<n;++i) p[i]=add(p[i],q[i]);
	p=exp(p);
	for(int i=n-1;i>=1;--i) p[i]=p[i-1];
	p[0]=0;
	for(int i=0;i<n;++i) f[i]=add(f[i],mod-p[i]);
	return f;
}
poly calc_dG(poly p,poly q,poly dq){
	int n=p.size();
	for(int i=0;i<n;++i) p[i]=add(p[i],q[i]);
	p=exp(p)*dq,p.resize(n);
	for(int i=n-1;i>=1;--i) p[i]=p[i-1];
	p[0]=1;
	for(int i=1;i<n;++i) p[i]=mod-p[i];
	return p;
}
poly calc_F(poly f,poly g,poly dg){
	int n=f.size();
	g=g*~dg,g.resize(n);
	for(int i=0;i<n;++i) f[i]=add(f[i],mod-g[i]);
	return f;
}

int main(){
	omg[0][0]=1,omg[0][1]=fpow(3,(mod-1)/N);
    omg[1][0]=1,omg[1][1]=fpow(omg[0][1],mod-2);
    fac[0]=fac[1]=1;
    inv[0]=inv[1]=1;
    ifac[0]=ifac[1]=1;
    for(int i=2;i<N;++i){
        omg[0][i]=mul(omg[0][i-1],omg[0][1]);
        omg[1][i]=mul(omg[1][i-1],omg[1][1]);
        fac[i]=mul(fac[i-1],i);
        inv[i]=mul(mod-mod/i,inv[mod%i]);
        ifac[i]=mul(ifac[i-1],inv[i]);
    }
	int n=read<int>()+1;
	poly f={0,1};
	for(int lim=4;lim<2*n;lim<<=1){
		f.resize(lim);
		poly f2=calc_F2(f);
		poly q=calc_Q(f,f2),dq=calc_dQ(f,f2);
		poly p=calc_P(q);
		poly g=calc_G(f,p,q),dg=calc_dG(p,q,dq);
		f=calc_F(f,g,dg);
	}
	f.resize(n);
	for(int i=1;i<n;++i) printf("%d\n",f[i]);
	return 0;
}