[NOI2002]贪吃的九头龙
[NOI2002]贪吃的九头龙
题目背景
传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”，但这只是 说它出生的时候有九个头，而在成长的过程中，它有时会长出很多的新头，头的 总数会远大于九，当然也会有旧头因衰老而自己脱落。
题目描述
有一天，有 M 个脑袋的九头龙看到一棵长有 N 个果子的果树，喜出望外， 恨不得一口把它全部吃掉。可是必须照顾到每个头，因此它需要把 N 个果子分成 M 组，每组至少有一个果子，让每个头吃一组。
这M个脑袋中有一个最大，称为“大头”，是众头之首，它要吃掉恰好 K 个 果子 ，而 且 K 个果子中理所当然地应该包括唯一的一个 最大的果子。 果子由 N-1 根树枝连接起来，由于果树是一个整体，因此可以从任意一个果子出发沿着树枝 “走到”任何一个其他的果子。
对于每段树枝，如果它所连接的两个果子需要由不同的头来吃掉，那么两个 头会共同把树枝弄断而把果子分开；如果这两个果子是由同一个头来吃掉，那么 这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然，吃树枝并不是很舒服的，因此每段树枝都有一个吃下去的“难受值”，而九头龙的难受值就是所 有头吃掉的树枝的“难受值”之和。
九头龙希望它的“难受值”尽量小，你能帮它算算吗？
例如图 1 所示的例子中，果树包含 8 个果子，7 段树枝，各段树枝的“难受 值”标记在了树枝的旁边。九头龙有两个脑袋，大头需要吃掉 4 个果子，其中必 须包含最大的果子。即 N=8，M=2，K=4：
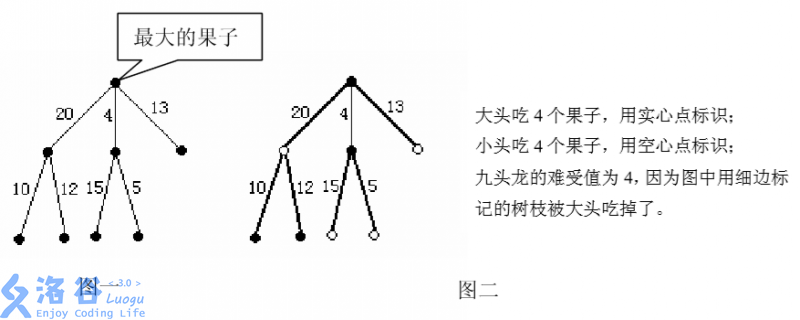
图一描述了果树的形态，图二描述了最优策略。
输入格式
输入文件 dragon.in 的第 1 行包含三个整数 N (1<=N<=300)，M (2<=M<=N)， K (1<=K<=N)。 N个果子依次编号 1,2,...,N，且 最大 的果子的 编 号 总 是 1。第 2 行到第 N 行描述了果树的形态，每行包含三个整数 a (1<=a<=N)，b (1<=b<=N)， c (0<=c<=)$10^5$，表示存在一段难受值为 c 的树枝连接果子 a 和果子 b。
输出格式
输出文件 dragon.out 仅有一行，包含一个整数，表示在满足“大头”的要求 的前提下，九头龙的难受值的最小值。如果无法满足要求，输出-1。
输入输出样例
8 2 4 1 2 20 1 3 4 1 4 13 2 5 10 2 6 12 3 7 15 3 8 5
4
说明/提示
该样例对应于题目描述中的例子。
题解
无解的情况很明显，当且仅当N-K<M-1时无解。
考虑用动态规划来解决。
首先通过观察我们发现这题的M只存在两种情况，M=2和M>2
如果M>2，那么通过交换必然有一种安排使得每个头都有至少一个果子吃且小头不会吃相邻的果子。
所以只需要考虑一个果子是否被大头吃，共两种状态。如果M=2，则必须算上小头吃的相邻果子的代价。
然后日常套路，设\(f[u][j]\)表示以\(u\)为子树有\(j\)个被大头吃最小代价，然后发现无法判断两个点之间是否都被大头吃，于是再加一维\(f[u][j][0/1]\)表示\(u\)号点是否被大头吃。
然后dp方程就是
然后惊奇的发现其实我们连样例都过不了(尴尬)
于是重新审视dp方程
我们需要每次dp前将之前的f数组备份下来，不然的话f值在dp中会越来越小(当然如果N也很小的话其实也没什么影响)
所以我们用tmp[j][0/1]来存f[u]数组的值，然后就能愉快的AC了
时间复杂度\(O(n^3)\)。
#include<bits/stdc++.h>
#define co const
#define il inline
template<class T>T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T>T read(T&x){
return x=read<T>();
}
using namespace std;
co int N=301;
int n,m,k;
int f[N][N][2],tmp[N][2];
vector<pair<int,int> > e[N];
void dfs(int x,int fa){
f[x][0][0]=f[x][1][1]=0;
for(unsigned i=0;i<e[x].size();++i){
int y=e[x][i].first,w=e[x][i].second;
if(y==fa) continue;
dfs(y,x);
memcpy(tmp,f[x],sizeof tmp),memset(f[x],0x3f,sizeof f[x]);
for(int j=0;j<=k;++j)
for(int t=0;t<=j;++t){
f[x][j][0]=min(f[x][j][0],min(f[y][t][0]+tmp[j-t][0]+(m==2)*w,f[y][t][1]+tmp[j-t][0]));
f[x][j][1]=min(f[x][j][1],min(f[y][t][1]+tmp[j-t][1]+w,f[y][t][0]+tmp[j-t][1]));
}
}
}
int main(){
read(n),read(m),read(k);
if(n-k<m-1) return puts("-1"),0;
for(int i=1,x,y,w;i<n;++i){
read(x),read(y),read(w);
e[x].push_back(make_pair(y,w)),e[y].push_back(make_pair(x,w));
}
memset(f,0x3f,sizeof f);
dfs(1,1);
printf("%d\n",f[1][k][1]);
return 0;
}
