SCOI2016 围棋

围棋

近日，谷歌研发的围棋 AI —— AlphaGo 以 4 : 1 的比分战胜了曾经的世界冠军李世石，这是人工智能领域的又一里程碑。与传统的搜索式 AI 不同，AlphaGo 使用了最近十分流行的卷积神经网络模型。在卷积神经网络模型中，棋盘上每一块特定大小的区域都被当做一个窗口。例如棋盘的大小为 \(5 \times 6\)，窗口大小为 \(2 \times 4\)，那么棋盘中共有 \(12\) 个窗口。此外，模型中预先设定了一些模板，模板的大小与窗口的大小是一样的。

对于一个模板，只要棋盘中有某个窗口与其完全匹配，我们称这个模板是被激活的，否则称这个模板没有被激活。我们要研究的问题是：对于给定的模板，有多少个棋盘可以激活它。为了简化问题，我们抛开所有围棋的基本规则，只考虑一个 $ n \times m $ 的棋盘，每个位置只能是黑子、白子或无子三种情况，换句话说，这样的棋盘共有 \(3^{nm}\) 种。此外，我们会给出 \(q\) 个 \(2 \times c\) 的模板。我们希望知道，对于每个模板，有多少种棋盘可以激活它。

强调：模板一定是两行的。

题解

考虑反面，用状压DP求出不合法的方案数，用\(3^{n*m}\)减去它就行了。

如果模板串只有一行，那么状态显然是\(f[i][j]\)，表示长度为\(i\)匹配到状态\(j\)未出现模板串的方案数。

考虑多了一行怎么做。显然不能两行都匹配上了，但是只有一行匹配上是可行的。那么就要记录二进制状态\(S\)表示上一行每个位置作为开头（或者结尾，一样的）是否完全匹配第一个串。为了方便转移\(S\)，还要记录二进制状态\(T\)表示这一行每个位置作为开头是否匹配第一个串，以及当前位置匹配到了第一个串的哪个位置。显然\(S\)和\(T\)不能有交集。

那么设\(f[i][j][S][T][x][y]\)表示填到了\((i,j)\)，上一行每个位置作为开头是否完全匹配第一个串的状态为\(S\)，这一行每个位置作为开头是否完全匹配第一个串的状态为\(T\)，与第一个串kmp匹配到了\(x\)，与第二个串kmp匹配到了\(y\)的方案数。然后直接加法转移即可。时空复杂度\(O(nm 2^{2(m-c+1)} c^2)\)，显然不可行。

比较显然的空间优化是滚动\((i,j)\)。然后我们发现\(S\)和\(T\)的有效状态位数之和一定是\(m-c+1\)，所以这两维状态可以合并成一个。考虑这个合并后的状态的实际意义，发现它就长成人们口口相传的轮廓线的模样。这个比方对程序实现来说形象准确，但是对初学者来说难于理解。最后的小优化是用kmp预处理出自动机，加速匹配。

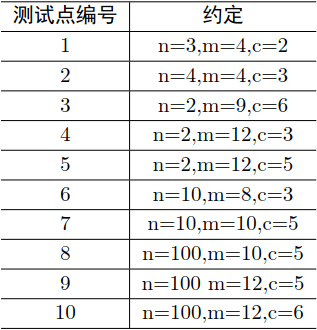
时间复杂度\(O(nm2^{m-c+1}c^2)\)，最后那个测试点是5e6.

co int mod=1e9+7;
int n,m,c,T,nxt[7],ta[6][3],tb[6][3],na,nb;
char a[8],b[8];
int id(char x) {return x=='B'?0:(x=='W'?1:2);}
int U,f[1024][6][6],g[1024][6][6],ans;
void up(int&x,int y) {x+=y;if(x>=mod)x-=mod;}
void clear() {for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)g[S][x][y]=0;}
void copy() {for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)f[S][x][y]=g[S][x][y];}
int main(){
	read(n),read(m),read(c),read(T);
	while(T--){
		scanf("%s%s",a+1,b+1);
		for(int i=1;i<=c;++i)a[i]=id(a[i]),b[i]=id(b[i]);
		for(int j=nxt[1]=0,i=2;i<=c;nxt[i++]=j){
			while(j&&a[j+1]!=a[i]) j=nxt[j];
			if(a[j+1]==a[i]) ++j;
		}
		na=nxt[c];
		for(int i=0;i<c;++i)for(int j=0,k;j<3;++j){
			for(k=i;k&&a[k+1]!=j;k=nxt[k]);
			if(a[k+1]==j) ++k;
			ta[i][j]=k;
		}
		for(int j=nxt[1]=0,i=2;i<=c;nxt[i++]=j){
			while(j&&b[j+1]!=b[i]) j=nxt[j];
			if(b[j+1]==b[i]) ++j;
		}
		nb=nxt[c];
		for(int i=0;i<c;++i)for(int j=0,k;j<3;++j){
			for(k=i;k&&b[k+1]!=j;k=nxt[k]);
			if(b[k+1]==j) ++k;
			tb[i][j]=k;
		}
		U=1<<(m-c+1);
		for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)f[S][x][y]=0;
		for(int i=f[0][0][0]=1;i<=n;++i){
			clear();
			for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)
				if(f[S][x][y]) up(g[S][0][0],f[S][x][y]);
			copy();
			for(int j=1;j<=m;++j){
				clear();
				for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)
					if(f[S][x][y]) for(int k=0,A,B,E;k<3;++k){
						E=S;
						if(j>=c) if(S>>(j-c)&1) E^=1<<(j-c); // init
						A=ta[x][k];
						if(A==c) E|=1<<(j-c),A=na;
						B=tb[y][k];
						if(B==c){
							if(S>>(j-c)&1) continue;
							B=nb;
						}
						up(g[E][A][B],f[S][x][y]);
					}
				copy();
			}
		}
		ans=1;
		for(int i=n*m;i;--i) ans=3LL*ans%mod;
		for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y) up(ans,mod-f[S][x][y]);
		printf("%d\n",ans);
	}
	return 0;
}

加强版

由于那个状态\(S\)跟棋子无关，所以可以增加棋子种类。另外可以规定某些位置不能填什么，某些位置必须填什么。