[中文翻译]JeffE Algo Ch6.6 线性时间求解强联通分量

本文原文见: https://jeffe.cs.illinois.edu/teaching/algorithms/#book
仅作为参考.

线性时间求解强联通分量

实际上, 有若干种算法可以让我们在\(O(V+E)\)的时间里面求解强连通分量. 关键就是看下面的这个观察:

引理6.2. 固定有向图\(G\)的深度优先遍历的顺序. 图\(G\)的每一个强联通分量\(C\)包含且仅包含一个在当前联通分量\(C\)里面没有父亲的节点. (这个节点的父亲可能在其他的强联通分量里面, 也可能根本没有父亲).

证明: 令\(C\)是\(G\)的任何一个强连通分量. 考虑属于同一个联通分量的两个点\(v,w\in C\)以及从\(u\)到\(v\)的路径. 在这条路径上, 每一个节点都可以到达\(w\), 因此也可以到达\(C\)中的每个节点; 根据对称性, 这个路径上面的每个节点同样可以到达\(v\), 因此也同样可以到达\(C\)中的每个节点. 因此我们说这条路径上面的每个节点也都在\(C\)里面.

我们把在联通分量\(C\)里面开始时间最早的节点记作\(v\). 如果\(v\)有父亲, 那么\(parent(v)\)就在\(v\)之前就开始了, 因此不可能在\(C\)里面.

现在, 令\(w\)是联通分量\(C\)中的另一个节点. 在DFS(v)被调用之前, 每一个\(C\)中的节点都是新的, 因此存在状态为新的节点组成的从\(v\)到\(w\)的路径. 根据引理6.1, 我们知道在深度优先遍历形成的森林中, \(w\)是\(v\)的子孙, 并且在树边\(u\to v\)上的每一个节点都会在\(C\)里面. 也就是, \(parent(w)\in C\). \(\square\)

刚刚的这个引理表明, 有向图\(G\)的形成的强联通分量中, 每一个强连通分量都是深度优先搜索形成的森林的一个联通的子树. 特别地, 对于每一个强连通分量, \(C\)中开始时间最早的顶点是\(C\)中所有顶点的最近公共祖先(lowest common ancestor). 我们称这个节点为联通分量\(C\)的根.

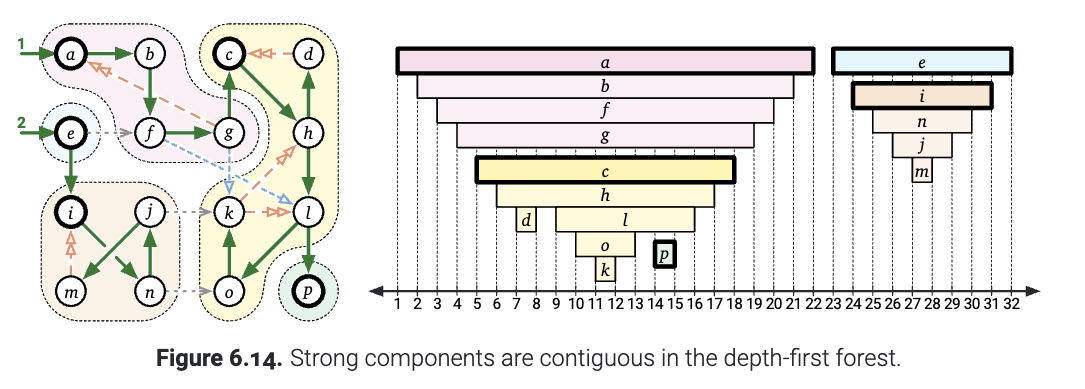
(图6.14 强联通分量在深度优先遍历的森林中是连续的)

接下来, 我会介绍两种算法. 它们都会为我们描绘一个直观的轮廓. 对于\(scc(G)\)的一个联通分量而言, 如果这个联通分量里面有汇点, 那么我们称它为汇分量(sink component). 等价地说, 如果 \(C\) 中任何顶点的到达范围恰好只有 \(C\), 则 \(C\) 是汇分量.我们可以按照下面的方式, 找到图中的强连通分量:

• 通过某种方式找到某些汇分量中的顶点 \(v\)(暂时还不知道怎么找, 后面会说)
• 找到从 \(v\) 可到达的顶点
• 从输入图中删除汇分量, 回到开始. 直到图中没有节点.
  虽然现在我们还没有明确如何得到汇分量, 但是我们已经可以知道算法的大致框架了!

Kosaraju和Sharir提出的算法

乍一看, 快速地找到一个图的汇分量有点困难. 但是, 如果我们先对它做一次DFS的话, 我们却很容易找到这个图的源分量(source component). 源分量代表\(G\)经过缩点之后形成的\(scc(G)\)中, 源点的那个分量.

引理6.3 在图\(G\)的任何一个后序遍历中, 最后遍历到的节点\(v\)在\(G\)的一个源分量中.

证明: 我们先任意取一个深度优先搜索的序列\(G\). 定义\(v\)是后序遍历的最后一个节点. 这样一来, 外围的DFSAll函数最后一次调用DFS一定是DFS(v). 此外, \(v\)是深度优先森林中一棵树的根. 因此\(v\)的子孙中任何一个节点\(x\), 一定满足\(x.post>v.pre\). 最后, \(v\)是这一部分强连通分量\(C\)的根.

为了证明方便, 考虑反证法. 假设有节点\(x\to y\)满足\(x\notin C, y\in C\). 并且, \(x\)可以到达\(y\), \(y\)可以到达\(v\). 这样一来, \(x\)就可以到达\(v\). 由于\(v\)是\(C\)的根, \(y\)是\(v\)的一个子孙. 因此\(v.pre<y.pre\). 这样的一条\(x\to y\)的边保证了\(y.pre<x.post\), 因此, \(v.pre<x.post\). 这就表明了\(x\)是\(v\)的子孙. 但是紧接着\(v\)可以通过树边到达\(x\), 就与我们的假设: \(x\notin C\)矛盾! \(\square\)

我们很容易验证对于任何一个有向图, \(rev(scc(G))=scc(rev(G))\). 因此, 在\(rev(G)\)中后序遍历的最后一个节点恰好在\(G\)的汇分量里面! 因此, 如果我们把图中的边反过来, 然后再按照后序遍历的逆序去调用DFS, 我们就每一次只会调用一个联通分量! (再次提醒: \(rev(G)\) 的后序遍历顺序与 \(G\) 的后序遍历不同.)

把上面的这些组合起来, 我们就有下图的算法. 这个算法在\(O(V+E)\)的时间内就可以计算, 标记图中的强连通分量. 这个算法在1978年被Rao Kosaraju发现, 但是他从来没有发表过它. 3年后, 这个算法又被Micha Sharir重新独立发现. (注: 有传言说, 相同的算法甚至在 Kosaraju 之前就出现在俄罗斯文献中, 但我还没有找到这种说法的可靠来源) Kosaraju-Sharir算法有两个阶段: 第一个阶段是在\(rev(G)\)上面进行深度优先搜索. 当一个节点结束了之后, 就会立即被放到栈上面. 在第二个阶段, 我们可以对原图按照栈上的顺序进行搜索(这时候无论是深度优先还是别的什么就不重要了). 搜索到的节点就会被标记在这个节点包含的联通分量里面.

下图显示了在例图上面运行的 Kosaraju-Sharir 算法. 只需对算法进行少量修改, 我们也可以在 \(O(V + E)\) 时间内计算出强分量图 \(scc(G)\).

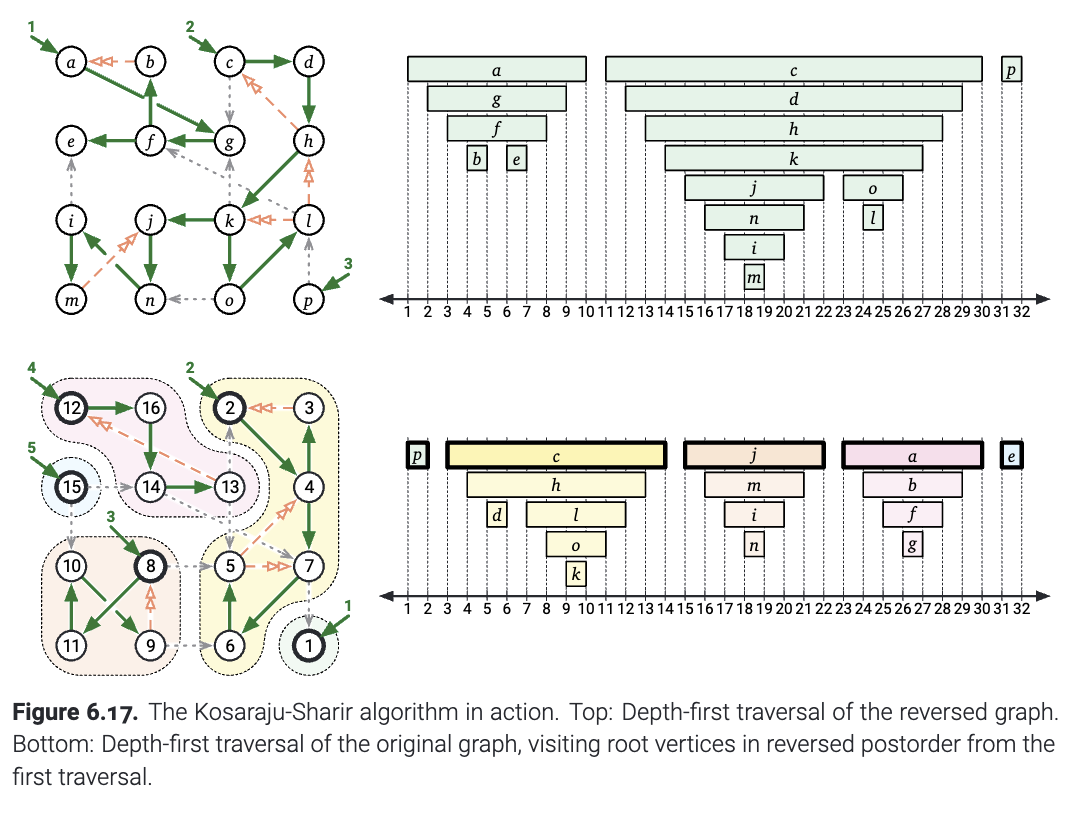
(图6.17 正在执行中的Kosaraju-Sharir算法, 上方: 反图的DFS; 下方: 原图上的DFS, 按照反图后序遍历的逆序访问节点)

❤️ Tarjan的算法

早在1972年, Bob Tarjan发表了一个线性时间计算强连通分量的算法.(注: 据传言, Kosaraju 显然是在一次算法课中发现了他的算法. 他本来应该讲解Tarjan的算法, 但他忘记了Tarjan算法是怎么做的了, 所以他不得不临时补一些东西. 这个故事唯一让我感到惊讶的是没有人提及 Sharir 或 Tarjan. ) 但是这个算法比上面介绍的更加微妙. 直观来看, Tarjan的算法会找到图\(G\)的一个源分量, 把它"删除", 然后递归继续寻找剩下的强连通分量. 不过, 整个计算过程在一次DFS就可以完成.

对于图\(G\)的一个给定的DFS顺序, 对于每个节点\(v\), 我们把\(low(v)\)定义为从\(v\)可以到达的最多经过一条非树边的路径. 我们很明显可以看出: \(low(v)\leq v.pre\), 因为\(v\)可以经过0条树边, 然后经过0条非树边. Tarjan注意到, 汇分量可以被\(low\)函数完全刻画.

引理6.4 一个节点\(v\)是图\(G\)的汇分量的一个根, 当且仅当\(low(v)=v.pre\)并且对于每个\(v\)的子孙\(u\), \(low(w)<w.pre\).

证明: 首先, 令\(v\)是满足\(low(v)=v.pre\)的一个节点. 对于\(v\)的一个节点的子孙\(w\), 一定没有\(w\to x\)并且\(x.pre<v.pre\). 另一方面, 节点\(v\)不可能到达所有满足\(y.pre>v.post\)的所有\(y\)节点. 特别的, \(v\)不能到达它的父亲(如果有的话), 因此\(v\)是强联通分量的根.

除此之外, 假设\(v\)的每个子孙\(w\)还满足\(low(w)<w.pre\), 那么子孙\(w\)就可以到达另一个节点\(x\)(节点\(x\)一定是\(v\)的另一个子孙), 满足\(x.pre<w.pre\). 因此, 根据归纳法, 每一个\(v\)的子孙可以到达\(v\). 由此可见，\(v\)的后代确实包含强联通分量\(C\), 其根为\(v\). 更进一步, 由于\(v\)不能到达\(C\)之外的节点, \(C\)一定是一个汇分量.

另一方面, 假设\(v\)是汇分量\(C\)的根, 那么只有在另一个节点\(w\in C\)的时候, \(v\)可以到达\(w\). 但 \(v\) 可以到达它的所有子孙, 并且 \(C\) 中的每个节点都是 \(v\) 的子孙. 因此 \(v\) 的子孙包含 \(C\). 如果对这个联通分量中的其他节点\(w\in C\), 如果\(low(w)=w.pre\), 那么\(w\)是\(C\)的另一个根. 这肯定是不可能的. \(\square\)

通过深度优先搜索计算每个顶点 \(v\) 的 \(low(v)\) 非常简单. 在DFS的过程中就可以完成. 见下图.

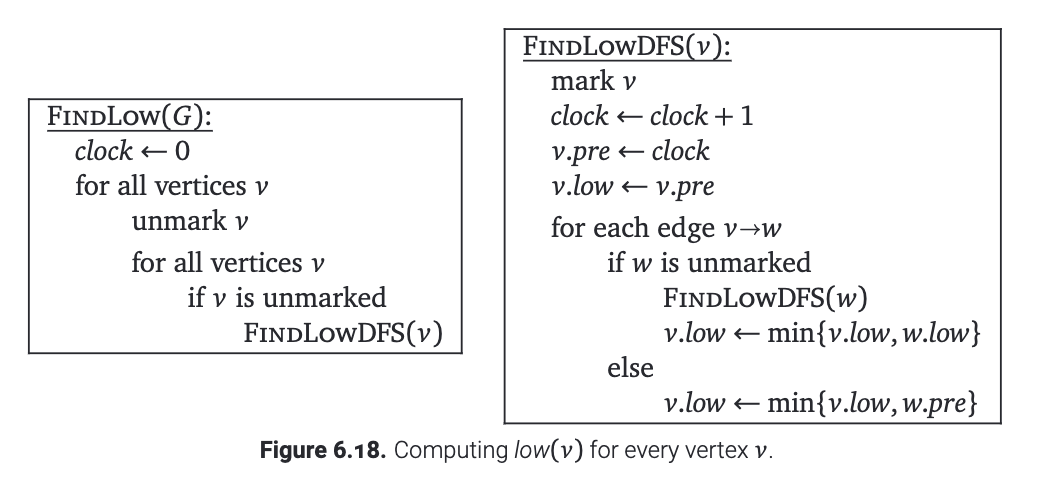
引理6.4说明了在运行FindLow之后, 我们可以在\(O(V+E)\)的时间内找出所有汇分量的根. (只要对整个图搜索一次就行了) 然后在 \(O(V + E)\) 额外时间内标记并删除这些汇分量(只要从每个汇分量的根考试搜索), 然后我们就可以递归求解别的节点了. 糟糕的事情是, 这个算法可能需要 \(V\) 次迭代, 每个只删除一个顶点，这样朴素的操作可能会让总运行时间变为\(O(VE)\).

为了加速这个算法, 除了递归的堆栈外, Tarjan 的算法还维护了一个辅助节点的栈. 每当开始访问一个新的顶点 \(v\) 时, 就把它压入堆栈. 每当我们访问完一个顶点 \(v\) 时, 我们都会将 \(v.low\) 与 \(v.pre\) 进行比较. 在我们第一次发现\(v.low=v.pre\)的时候, 就有下列的三个情况:

• 节点\(v\)是汇节点\(C\)的一个根.
• 所有\(C\)中的节点在这个辅助栈的排列是连续的.
• 在这个辅助栈中, 最深的节点是\(v\).

此时, 我们可以通过将 \(C\) 中的顶点一一弹出辅助堆栈来识别它们, 当弹出 \(v\) 时, 就可以停止继续弹出了. 我们这时候就得到了联通分量的所有内容.

现在, 我们可以把\(C\)中所有的节点都删除掉, 然后继续计算剩余图中的联通分量. 但是这就有点浪费了. 因为删除了之后, 再找的时候我们又要把访问\(v\)之前的那些信息一字不落的算回来. 相反, 我们标记 \(C\) 中的每个顶点，将 \(v\) 标记为这个强分量的根，然后在接下来的DFS中忽略被标记的顶点. 正是这样, 我们就将将 \(low(v)\) 的定义更改为 "与 \(v\) 相同的联通分量的所有顶点中, \(v\) 可以通过树边路径（后跟最多一个非树边）到达的最小起始时间". 但为了证明正确性，实际上忽略标记的节点并不会影响这个算法的正确性.

最后, 下图展示的是Tarjan的算法. 对于FindLow函数(见图6.18)的更改用加粗的红色标识. 我们要分析算法的运行时间, 可以分为两部分. 由于每个顶点被推入 \(S\) 一次, 并从 \(S\) 弹出一次. 所以维护辅助堆栈所花费的总时间(红色)是\(O(V)\). 如果我们忽略辅助堆栈维护, 这个算法的其余部分只是一个标准的深度优先搜索.因此我们得出结论, 该算法运行时间为 \(O(V + E)\).