校赛G题一个更朴素的做法

猫猫虫有一个定义如下的数列：

\( a_{n} = \begin{cases} 0 & n = 1 \\ a_{\left\lfloor \frac{n}{2} \right\rfloor} + (-1)^{\frac{n(n + 1)}{2}} & n \geq 2 \end{cases} \)
猫猫虫要求saki计算该数列前 \(n\) 项绝对值的和，即求：
\( \sum_{i=1}^{n} |a_{i}| \)
输出答案对 \(10^{9} + 7\) 取模后的结果。

对于 100% 的测试数据：

• \(1 \leq n \leq 10^{18}\)
• \(1 \leq T \leq 5 \times 10^5\)

（以上题面摘自刘队原创好题猫猫虫的序列）

观察递推式，不难发现

• \(a_{n/2}\)项：第2,3项由第1项决定，第4,5项由第2项决定，第6,7项由第3项决定……非常自然地，我们得到了一颗二叉树；
• ±1项：-1的指数为1到n的等差数列，奇偶性为奇，奇，偶，偶，奇，奇……显然，4位一循环。

我们将二叉树画出：

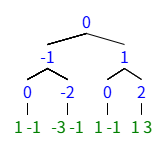
我们非常容易发现，如果维护的信息为“本层每种数的个数（正负不论）”，那么如果上一层给定，很容易唯一确定下一层。

如：第二层有两个1，由于每个数固定产生一个+1的儿子，一个-1的儿子，两个1就产生两个0和两个2.由此可继续推下一层。其中0稍显特殊，加一减一都为1。

于是，我们自然想到了一种\(O(T\log^2 n)\)的做法：

假如我们的n是12，先观察在树上的跑法

——\(12_{OCT}=1100_{BIN}\)，0往左，1往右。

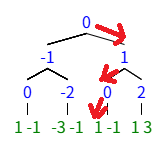
先用\(O(log^2 n)\)时间预处理出蓝色部分的满二叉树部分和。

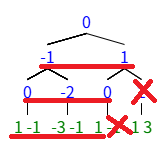
然后，对于绿色部分，由于我们只取划红线部分，可以在上述跑的过程中，把不要的部分及时删除。这，又是一次\(O(log^2 n)\)时间，但它是对于每一组数据的，故总复杂度\(O(Tlog^2 n)\)

然而，这个复杂度不能通过。难道这种做法真的不行吗？

我们继续优化，考虑：是否可以将每种树的答案预处理出来？

经过思考，这是可行的。我们设定\(a[root][ceng]\)为以\(root\)为根，\(ceng\)层树的答案。可以看到，它是唯一的。

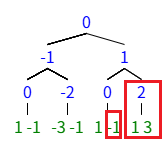
于是，我们的求解就变成了，在树上跑的过程中，每次扔掉东西的时候，直接减去其子树的树叶部分。对于\(12\)的情况，就是以\(a[0][4]\)的总体（图中所有点构成的满二叉树），先减掉\((a[2][2]-a[2][1])\)（大红框的叶子），再减掉\((a[1][1]-a[1][0])\)（小红框的叶子）。

这样，就得到正确结果。

代码如下。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1000000007;
int TR[200][200];
int a[200][200];
void init(int root)
{
	memset(TR,0,sizeof(TR));
	TR[1][root]=1;
	int sum=0;
	for(int ceng=1;ceng<=64;ceng++)
	{
		sum=0;
		TR[ceng][0]=(TR[ceng][0]+TR[ceng-1][1])%mod;
		TR[ceng][1]=(TR[ceng][1]+TR[ceng-1][0])%mod;
		for(int j=1;j<=128;j++)
		{
			TR[ceng][j]=(TR[ceng][j]+TR[ceng-1][j-1])%mod;
			TR[ceng][j]=(TR[ceng][j]+TR[ceng-1][j+1])%mod;
		}
		for(int j=0;j<=128;j++) sum=(sum+TR[ceng][j]*j)%mod;
		a[root][ceng]=(a[root][ceng-1]+sum)%mod;
	}
}
signed main()
{
	int T,n;
	for(int i=0;i<=64;i++) init(i);
	scanf("%lld",&T);
	while(T--)
	{
		scanf("%lld",&n);
		int t=0,n0=n;
		while(n)
		{
			t++;
			n>>=1;
		}
		int r=0,ceng=1,D=0; 
		for(int i=t-2;i>=0;i--)
		{
			ceng++;
			int N=n0>>i;
			int re=N%4;
			if(re==1||re==2) r++;
			else r--;
			if(!(N&1))
			{
				int del;
				if(re==1||re==2) del=abs(r-2);
				else del=abs(r+2);
				D=(D+a[del][i+1]-a[del][i]+mod)%mod;
			}
		}
		printf("%lld\n",(a[0][ceng]-D)%mod);
	}
	return 0;
}

刘队常言“给十个小时，算法竞赛的题都能做出来。”这诚然夸张，就这场来说，确实如此。事后观之，这场的题包括这题实际我都想到正确做法了，甚至有未正式出在比赛里的题也被我想出来了。