分层图简介
简介
分层图,可以理解为把原来的图拆成了多层图,层与层之间只能通过规定的路转移。
一般用于在一个点可以进行某种操作从而改变图的形态,或是点有着某种特殊属性导致相连的边不是随时随地都可以走的情况下,拆成多层便于转化某些操作。
明显的特点是因为空间限制,层数和点数的乘积不会特别大。
说起来抽象,还是从题目讲起。
AT_abc395_e [ABC395E] Flip Edge
注意不要读错题,花费 \(X\) 的代价是反转所有边,而非反转某条边,因为这个浪费 5 min。
分层最短路模板,发现图实际上只有原图和反图两种形态,我们考虑建一遍原图,再建一遍反图,这样一个点被我们拆成了两个点,一个属于原图,一个属于反图,而这两个点我们可以连一条双向边,边权为 \(X\),这样再跑 dij,最后在原图的点 \(n\) 和反图的点 \(n\) 取 min 即可。
利用这种方法,我们把反转图的操作转化为了从正图的这个点走向了反图的这个点,同时花费了 \(X\)。
具体实现时我们可以用 \(i+n\) 点表示 \(i\) 在反图上点的编号。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 2e5+30;
const int maxm = 2e5+30;
int n,m,x;
vector<int> e[maxn<<1],w[maxn<<1];
int dis[maxn<<1];
bool vis[maxn<<1];
struct node{
int p,w;
bool operator < (const node &y) const {
return w > y.w;
}
};
priority_queue<node> q;
inline void dij(int s) {
for (int i = 1; i <= 2*n; i++) dis[i] = 1e18;
memset(vis,0,sizeof(vis));
dis[s] = 0;
q.push({s,0});
while (q.size()) {
node t = q.top();
q.pop();
int u = t.p;
if (vis[u]) continue;
vis[u] = true;
for (int i = 0; i < e[u].size(); i++) {
int v = e[u][i],W = w[u][i];
if (dis[v]>dis[u]+W) {
dis[v]=dis[u]+W;
q.push({v,dis[v]});
}
}
}
cout << min(dis[n],dis[n+n]) << '\n';
}
signed main() {
#ifdef LOCAL
freopen("D:/codes/exe/a.in","r",stdin);
freopen("D:/codes/exe/a.out","w",stdout);
#endif
cin >> n >> m >> x;
for (int i = 1; i <= m; i++) {
int u,v;
cin >> u >> v;
e[u].push_back(v);
w[u].push_back(1);
e[v+n].push_back(u+n);
w[v+n].push_back(1);
}
for (int i = 1; i <= n; i++) {
e[i].push_back(i+n);
w[i].push_back(x);
e[i+n].push_back(i);
w[i+n].push_back(x);
}
dij(1);
return 0;
}
P4822 [BJWC2012] 冻结
我们直接建 \(0\sim k\) 共 \(k+1\) 层图,每一层的编号代表剩余几张 Spellcard。
然后连边。除了层内正常连边外,每条边 \((u,v)\) 还需要连 \(i+1\) 层的 \(u\) 和 \(i\) 层的 \(v\)。
最后跑最短路,检查每层 \(v\) 即可。
至于每条道路上最多用一张 Spellcard 的限制根本不用管。因为边权为正,最短路一定不可能走一条边两次。
利用分层图,我们把使用 Spellcard 转化为了花费 \(0\) 到了下一层这条边的终点。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e3+10;
const int maxm = 4e5+20;
int n,m,k;
struct edge{
int to,nxt,w;
}e[maxm];
int head[maxn],tot;
inline void add(int u,int v,int w) {
e[++tot].to = v;
e[tot].nxt = head[u];
e[tot].w = w;
head[u] = tot;
}
struct node{
int w,p;
bool operator < (const node &y) const{
return w > y.w;
}
};
priority_queue<node> q;
int dis[maxn];
bool vis[maxn];
inline void dij() {
memset(dis,0x3f,sizeof(dis));
dis[1] = 0;
q.push({0,1});
while (!q.empty()) {
node t = q.top();
q.pop();
if (vis[t.p]) continue;
vis[t.p] = true;
for (int i = head[t.p]; i; i = e[i].nxt) {
int v = e[i].to,w = e[i].w;
if (vis[v]) continue;
if (dis[v] > dis[t.p] + w) {
dis[v] = dis[t.p] + w;
q.push({dis[v],v});
}
}
}
int ans = 0x3f3f3f3f;
for (int j = 0; j <= k; j++) {
ans = min(ans,dis[n+j*n]);
}
cout << ans << '\n';
}
signed main() {
#ifdef LOCAL
freopen("E:/codes/exe/a.in","r",stdin);
freopen("E:/codes/exe/a.out","w",stdout);
#endif
cin >> n >> m >> k;
for (int i = 1; i <= m; i++) {
int u,v,w;
cin >> u >> v >> w;
for (int j = 0; j <= k; j++) {
add(u+j*n,v+j*n,w);
add(v+j*n,u+j*n,w);
}
for (int j = 0; j < k; j++) {
add(u+j*n,v+(j+1)*n,w/2);
add(v+j*n,u+(j+1)*n,w/2);
}
}
dij();
return 0;
}
P7297 [USACO21JAN] Telephone G
思路新奇的分层图最短路。
首先如果我们对品种开桶,然后把两种品种里的所有点两两连边,那么直接 \(O(n^2)\) 打飞。
发现 \(k\) 很小,只有 \(50\),考虑转化限制。
我们建立 \(k+1\) 层图,其中 \(1\sim k\) 层表示品种,每层的相邻两点之间连一条边权为 \(1\) 的双向边。第 \(k+1\) 层点之间不要连任何边,这一层的点的最短路数据才是从 \(1\) 传信息到这个点的最小花费。
然后最妙的就来了:
我们记 \(a_i\) 表示 \(i\) 的品种,从 \(a_i\) 层的 \(i\) 向 \(k+1\) 层的 \(i\) 连边权为 \(0\) 的单向边。然后记 \(a_i\) 能够交谈的品种有 \(b_j\),那么从 \(k+1\) 层的 \(i\) 向 \(b_j\) 层的 \(i\) 连一条边权为 \(0\) 的单向边。
这样有什么用呢?假如我们现在有点 \(1\) 品种为 \(1\),点 \(2\) 品种为 \(2\),点 \(3\) 品种为 \(3\),仅有品种 \(1\) 能向 \(3\) 传话。那么这个 \(1\to3\) 的更新过程就是从 \(k+1\) 层的 \(1\) 到 \(3\) 层的 \(1\),然后到 \(3\) 层的 \(2\),由于这一层的 \(2\) 没有向 \(k+1\) 层连边所以略过。再走到 \(3\) 层的 \(3\),再走向 \(k+1\) 层的 \(3\),更新答案。而其他的非法路径我们都不会去尝试。
样例图解:
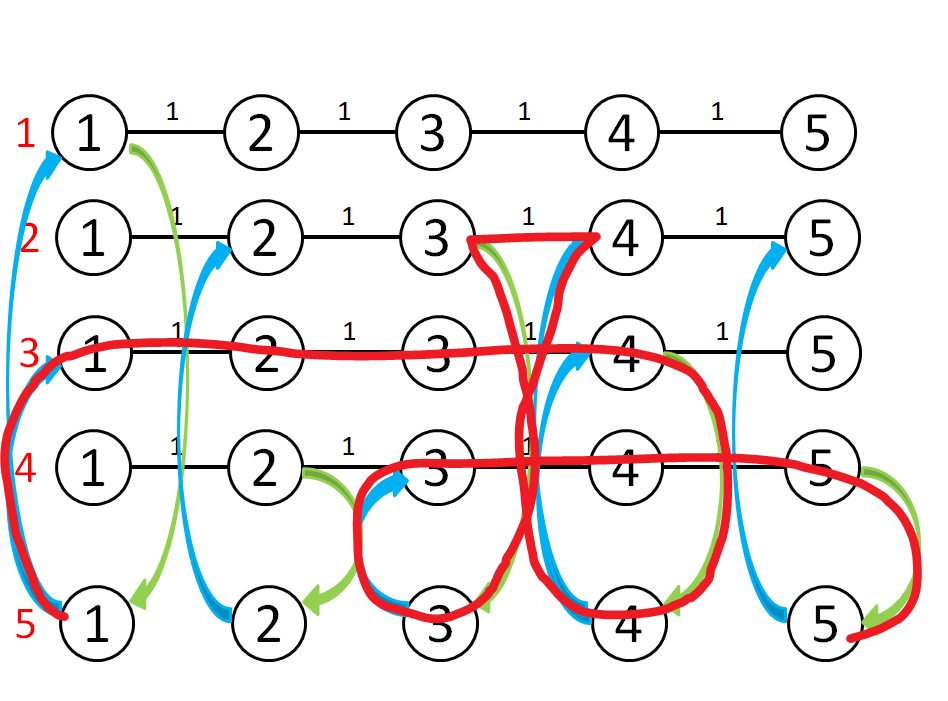
注意边权只有 \(0,1\),使用双端队列 bfs 比 dij 更快。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e6+10;
int n,k;
int b[maxn];
struct edge{
int v,w;
};
vector<edge> e[maxn];
vector<int> c[maxn];
int dis[maxn];
deque<int> q;
inline void bfs(int s) {
memset(dis,0x3f,sizeof(dis));
dis[s] = 0;
q.push_front(s);
while (!q.empty()) {
int u = q.front();
q.pop_front();
for (auto i : e[u]) {
int v = i.v,w = i.w;
if (dis[v] != 0x3f3f3f3f) continue;
if (w == 0) {
dis[v] = dis[u];
q.push_front(v);
}else if(w == 1) {
dis[v] = dis[u]+1;
q.push_back(v);
}
}
}
if (dis[k*n+n] != 0x3f3f3f3f) cout << dis[k*n+n] << '\n';
else cout << -1 << '\n';
}
int main() {
#ifdef LOCAL
freopen("D:/codes/exe/a.in","r",stdin);
freopen("D:/codes/exe/a.out","w",stdout);
#endif
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> b[i];
e[(b[i]-1)*n+i].push_back({k*n+i,0});
c[b[i]].push_back(i);
}
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= k; j++) {
char x;
cin >> x;
if (x == '1') {
for (auto v : c[i]) {
e[k*n+v].push_back({(j-1)*n+v,0});
}
}
}
}
for (int i = 0; i < k; i++) {
for (int j = 1; j < n; j++) {
e[i*n+j].push_back({i*n+j+1,1});
e[i*n+j+1].push_back({i*n+j,1});
}
}
bfs(k*n+1);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号