强化学习基础系列(一)：强化学习基本定义

0x1 强化学习简介

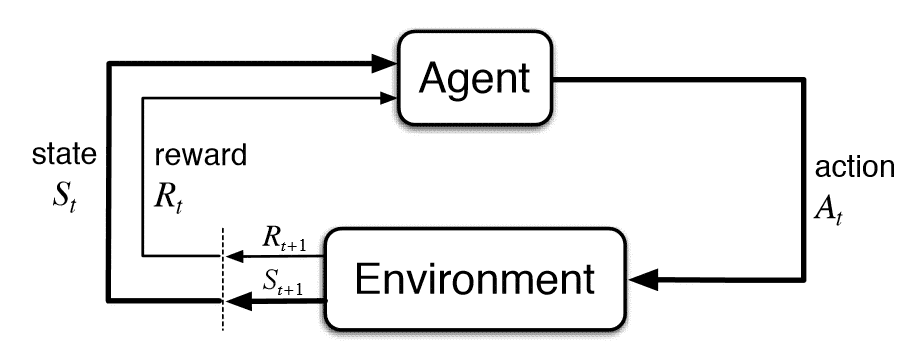
强化学习(Reinforcement Learning, RL)是机器学习(Machine Learning, ML)的三大分支之一。在一个强化学习问题中, 有一个决策者, 我们通常称之为智能体(agent), 它所交互的区域叫做环境(environment, env), 它所处的当前环境称为状态(state), agent观察到的这个环境状态称为(observation,obs), agent会根据observation, 根据自己的策略(policy)执行动作(action), 根据agent的action, 给agent相应的奖励(reward), 并同时进入到下一个state。就这样不断地重复, 直到env到达了一个终止状态(terminal state)(注：有的环境不存在终止状态)。agent在从开始到终止状态中所获得的reward之和。称之为回报(return)。agent的目的, 就是优化自己的policy,使得它的return最大。在没有特殊说明的情况下, 在本博客中提到的环境state等价于agent的observation，也就是env是完全可观察环境。如图, 是强化学习的状态转移图。强化学习具有以下特点：

• 以reward作为监督信号
• 反馈具有延后性(不是及时的)
• 处理的数据为序列数据而非独立同分布

0x2 MDP简介

RL是建立在​环境具有马尔科夫性的假设上的，即下一个状态的产生只取决于当前的状态，而与之前的状态无关。即

\[P[S_{t+1}|S_t] = \mathbb P[S_{t+1}|S_1,...,S_t] \]

​马尔可夫决策过程(Markov Decision Process, MDP)正式描述了强化学习的决策过程, MDP可以定义为<\(S,A,P,R,\gamma\)>, 分别表示state集合、action集合、状态转化概率、reward函数、衰减率。RL的policy有两种，确定性策略(deterministic policy)和随机性策略(stochastic policy)，前者表示对于一个策略\(\pi\),给定状态\(s\),策略会给出一个动作\(a\), 记为\(\pi(s)=a\)。而后者对于一个策略\(\pi\)， 给定状态\(s\), 会给出执行动作空间里的每个动作的概率分布, 记为\(\pi(a|s)=\mathbb P[A_t=a|S_t=s]\), 在此，我们同时也假设了策略\(\pi\)也符合马尔可夫假设，即此时采取动作\(a\)的概率只和当前的状态\(s\)有关，而与其他要素无关。我们可以定义出环境转移的概率为

\[P_{ss^{'}} = \mathbb P[S_{t+1} =s^{'}|S_t=s] \]

在状态\(s\)处执行\(a\)的转移概率，可以定义为

\[P_{ss^{'}}^a = \mathbb P[S_{t+1} =s^{'}|S_t=s,A_t=a] \]

使用策略\(\pi\)，在状态\(s\)处执行动作后的转移概率，可以定义为

\[P_{ss^{'}}^{\pi} = \sum_{a \in A} \pi(a|s)\mathbb P_{ss^{'}}^a \]

在状态\(s\)处执行\(a\)，能获得的\(r\)的期望，可以定义为

\[R_{s}^a = \mathbb E[R_{t+1} = r|S_t=s,A_t=a] \]

使用策略\(\pi\)，在状态\(s\)处执行动作后能获得的\(r\)的期望，可以定义为

\[R_{s}^{\pi} = \sum_{a \in A} \pi(a|s)R_{s}^a \]

我们使用状态价值函数(value function) \(V_{\pi}(s)\)来衡量一个状态s的好坏，其值为从状态\(s\)开始的执行策略\(\pi\)的return的期望，表示为

\[V_{\pi}(s) = \mathbb {E}_{\pi}[G_t|S_t=s] \]

我们使用动作状态价值函数(Q function) \(Q_{\pi}(s,a)\)来衡量一个状态\(s\)下采取特定\(a\)的好坏，其值为从状态\(s\)开始执行特定\(a\)(与策略\(\pi\)无关)后，执行策略\(\pi\)的return的期望，表示为

\[Q_{\pi}(s,a) = \mathbb {E}_{\pi}[R_{t+1} + \gamma(V_{\pi}(S_{t+1}))|S_t=s, A_t=a] \]

0x3 贝尔曼期望方程与最优方程

贝尔曼期望方程(Bellman Expectation Equations), 将状态值函数\(V(s)\)与动作值函数\(Q(s,a)\)、将当前的值函数\(V(s)\)与之后状态\(V(s^{’})\)、将当前的动作值函数\(Q(s,a)\)与之后的动作的值函数\(Q(s^{’},a^{’})\)联系起来。其整体过程可以用这张图表示。

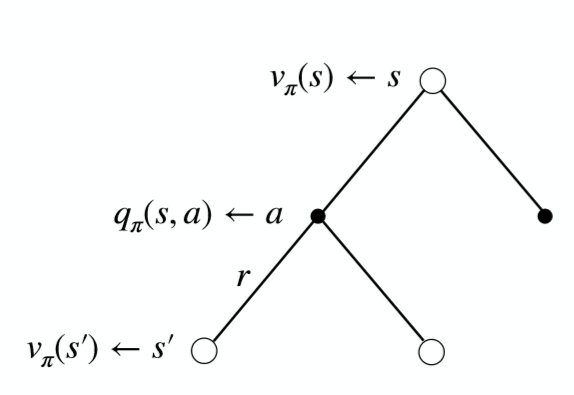
状态值函数\(V(s)\)与动作值函数\(Q(s,a)\)的关系

\[V_{\pi}(s)=\sum_{a \in A} \pi(a|s) Q_{\pi}(s,a) \]

\[Q_{\pi}(s,a)=R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a V_{\pi}(s^{'}) \]

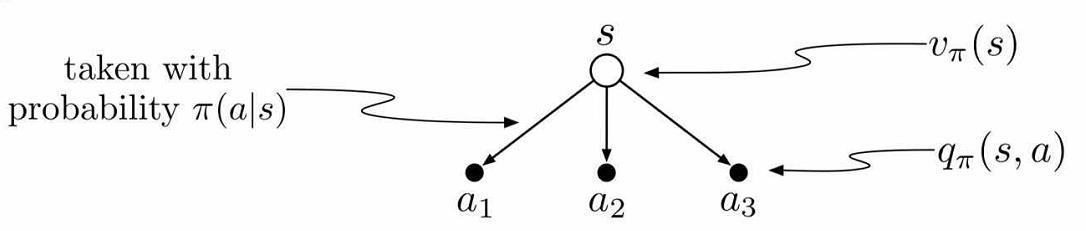
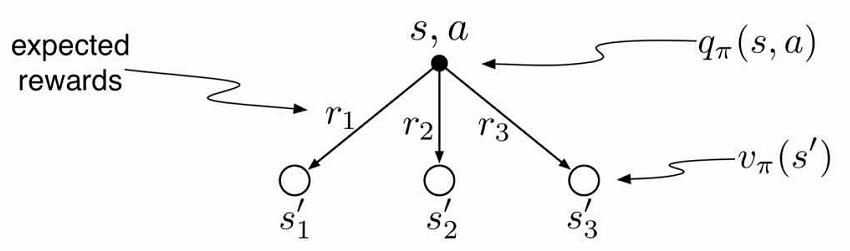
联系\(V(s)\)与\(V(s^{’})\)

将以上两式相结合，立刻得到

\[V_{\pi}=\sum_a \pi(a|s) (R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a V_{\pi}(s^{'})) \]

联系\(Q(s,a)\)与\(Q(s^{’},a^{’})\)

同理

\[Q_{\pi}(s,a)=R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a \sum_{a^{'} \in A} \pi(a^{'}|s^{'}) Q_{\pi}(s^{'},a^{'}) \]

最优价值函数

\[V^{*}(s)=\max_{\pi}V_{\pi}(s) \]

\[Q^{*}(s,a)=\max_{\pi}Q_{\pi}(s,a) \]

贝尔曼最优方程

贝尔曼最优方程是在贝尔曼期望方程的基础上推理得到的。在策略\(\pi\)达到最优时，状态价值函数V与动作价值函数Q取最大a是相等的

\[V^{*}(s)=\max_{a} Q^{*}(s,a) \]

\[Q^{*}(s,a)=R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a V^{*}(s^{'}) \]

\[V^{*}(s)=\max_{a}(R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a V^{*}(s^{'})) \]

\[Q^{*}(s,a)=R_{s}^a+\gamma \sum_{s^{'} \in S} P_{ss^{'}}^a \max_{a} Q^{*}(s^{'},a^{'}) \]

​如果我们完全直到环境信息，则问题可以转化为一个规划问题，通过动态规划求解，但大部分时候我们不知道转移概率、reward函数，不能直接通过贝尔曼方程求解。