DBSCAN算法（转）

一、什么是DBSCAN算法

DBSCAN算法指定一个半径ε和一个数量M,它将空间中的点分成3种:核心点指在半径范围ε内含有超过M个相邻点的点;边界点指非核心点，但在核心点半径ε范围内的点;其余的点称为噪声。DBSCAN遍历每个点,判断每个点是否为核心点,寻找每个核心点周围的所有点,并将周围的点和相应核心点标记为同一个类别。
在遍历整个样本集的过程中,首先根据一个点的半径ε范围内的点的数量判断其是否为核心点。若是核心点,就将半径ε范围内的点和该点标记为同一类,并对每个周围的点做相同操作,再次查看是否为核心点。持续该过程,直到每个点都被遍历过。此时,未被分类的点就是噪声。DBSCAN算法需要对半径ε和阀值M进行调参。

没有进行DBSCAN算法：

 

 

图中的epsilon指的是半径，minPoints指的是在半径为1的空间里有四个小球即可扩散

进行过DBSCAN算法：

 

 

二、DBSCAN算法的算法步骤：
（1）计算所有点的ε邻域： 对于数据集中的每一个点P，计算其ε邻域中有多少个邻居。这个邻居数量的阈值通常由一个参数MinPts定义。
（2）标记核心点： 如果一个点的ε邻域中的点的数量大于或等于MinPts，那么这个点就被标记为核心点。
（3）寻找密度相连的点： 对于每一个核心点，寻找所有与其密度相连的点。如果点P在点O的ε邻域中，并且O是一个核心点，那么P就是一个与O密度相连的点。
（4）标记噪声点和边界点： 没有被标记为核心点的点被标记为噪声点。与某个核心点密度相连但不是核心点的点被标记为边界点。
为每一个核心点或与其密度相连的点赋予一个独立的簇标签： 为每一个核心点或与其密度相连的点赋予一个独立的簇标签。如果一个点与多个核心点密度相连，那么它将被赋予第一个找到的核心点的簇标签。
（5）噪声点形成独立的簇： 所有的噪声点形成一个独立的簇。

三、DBSCAN算法的优缺点如下：

优点如下所示：
1. 不需要预设聚类数：DBSCAN不需要事先指定聚类的数量，这使得算法更加灵活。
2. 识别噪声点：DBSCAN能够识别并处理噪声点，这对于包含异常值的数据集来说非常有用。
3. 任意形状的聚类：DBSCAN可以发现任意形状的聚类，不仅限于球形或圆形。
4. 密度基础：聚类是基于密度的连通性，这使得算法能够识别出由密度变化定义的聚类。
5. 参数较少：只需要设置两个参数（ε和MinPts），相比其他算法，参数调整较为简单。
缺点如下所示：
1. 参数敏感性：ε和MinPts的选取对聚类结果有很大影响，不恰当的参数可能导致聚类效果不佳。
2. 对高维数据效率低：随着数据维度的增加，计算邻域点的复杂度增加，导致算法效率降低。
3. 对均匀密度的数据效果不佳：如果数据集中的聚类具有相似的密度，DBSCAN可能无法很好地区分它们。
4. 边界点处理：DBSCAN对边界点的处理可能不如其他一些算法，因为它可能将边界点归入最近的聚类，这可能不是最优的。
5. 计算复杂度：对于大数据集，DBSCAN可能需要较长的运行时间，尤其是在计算每个点的ε邻域时。
6. 空间复杂度：在存储邻域信息时，DBSCAN可能需要较高的空间复杂度。
7. 对密度变化敏感：如果数据集中的聚类密度差异较大，DBSCAN可能将它们识别为不同的聚类，即使它们在其他方面是相似的。
8. 不适合大规模数据集：对于非常大的数据集，DBSCAN可能不是最佳选择，因为它需要存储和处理大量的邻域信息。

四、代码

1、使用Matplotlib观察所有样本根据连续值age、bmi和charges绘制的图像,相关代码如下：

import matplotlib.pyplot as plt
# 定义一个函数用于绘制3D散点图
def graph3d(data, x, y, z):
# 创建一个新的图形，并添加一个3D子图
ax = plt.figure().add_subplot(111, projection='3d')
# 使用散点图绘制3D数据点
# s参数控制点的大小，c参数控制点的颜色，marker参数控制点的形状
ax.scatter(data[x], data[y], data[z], s=10, c='r', marker='.')
# 设置x轴的标签
ax.set_xlabel(x)
# 设置y轴的标签
ax.set_ylabel(y)
# 设置z轴的标签
ax.set_zlabel(z)
# 显示图形
plt.show()
# 假设train是一个包含年龄、体重指数和医疗费用数据的DataFrame
# 调用graph3d函数，绘制年龄、体重指数和医疗费用的3D散点图
# 这里假设'age', 'bmi', 'charges'是DataFrame train中的列名
graph3d(train, 'age', 'bmi', 'charges')

 

 

 

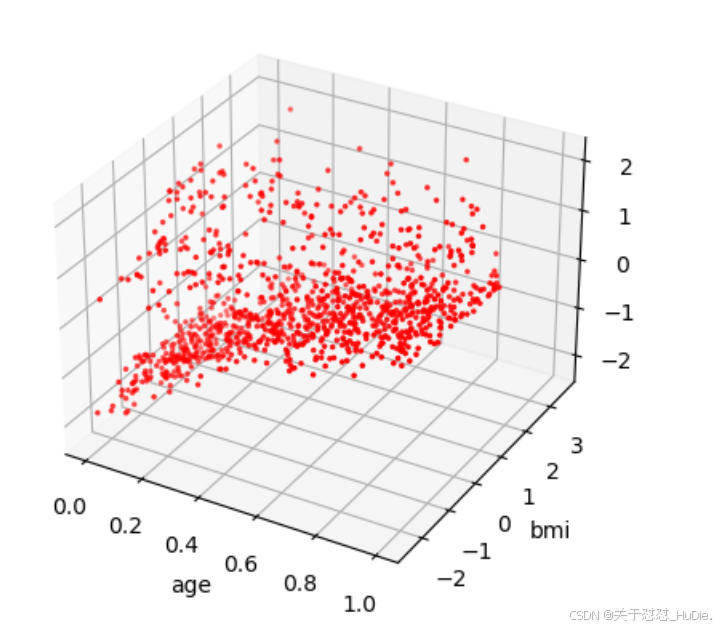
图6-4 空间中的分布

可以发现,数据大致分布于三个曲面。当数据具有明显的分层时,适合使用DBSCAN聚类方法对数据进行分类，从而对不同类别的样本分别进行分析。

2、DBSCAN算法需要对半径ε和阀值M进行调参。在本例中,由于需要将样本分为3类,因此调整ε=0.45,M=10,相关代码如下所示

import sklearn.cluster as cluster
# 定义一个DBSCAN聚类函数，用于对数据进行聚类分析
def dbscan(data, features=None):
# 创建DBSCAN聚类对象，eps是邻域的半径，min_samples是形成密集区的最小样本点数
clusterer = cluster.DBSCAN(eps=0.45, min_samples=10)
# 如果指定了特征，则只使用这些特征进行聚类
x = data
if (features):
x = data[features]
# 对数据进行聚类，并返回每个样本的聚类标签
y = clusterer.fit_predict(x.values)
# 将聚类标签添加到原始数据中
data["type"] = y
# 返回包含聚类标签的数据
return data

# 从原始训练数据train中选择特定的列进行DBSCAN聚类分析
# 这里选择了'age', 'bmi', 'charges'这三列
train1 = train[['age', 'bmi', 'charges']].copy(deep=True)

# 调用dbscan函数进行聚类，并将聚类结果的'type'列返回到原始训练数据train中
train["type"] = dbscan(train1)["type"]

# 打印唯一的聚类标签，以查看数据被分为几个不同的聚类
print(train["type"].unique())

 

运行结果：

 

 

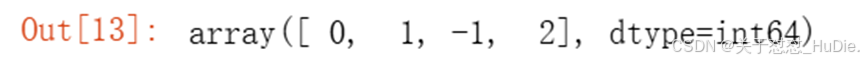
3、聚类的结果可以使用Matplotlib进行观察,相关代码如下所示：

import matplotlib.pyplot as plt
import sklearn.cluster as cluster

# 定义一个函数用于绘制3D散点图，展示聚类结果
def graph3dc(train, x, y, z, type_name='type'):
# 创建一个新的图形，并添加一个3D子图
ax = plt.figure().add_subplot(111, projection='3d')

# 根据聚类标签绘制不同颜色的散点图
# 假设聚类标签为0，绘制红色散点图
data = train[train[type_name] == 0]
ax.scatter(data[x], data[y], data[z], s=10, c='r', marker='.')

# 假设聚类标签为1，绘制绿色散点图
data = train[train[type_name] == 1]
ax.scatter(data[x], data[y], data[z], s=10, c='g', marker='.')

# 假设聚类标签为2，绘制蓝色散点图
data = train[train[type_name] == 2]
ax.scatter(data[x], data[y], data[z], s=10, c='b', marker='.')

# 设置x轴的标签
ax.set_xlabel(x)
# 设置y轴的标签
ax.set_ylabel(y)
# 设置z轴的标签
ax.set_zlabel(z)

# 显示图形
plt.show()

# 调用graph3dc函数，绘制年龄、体重指数和医疗费用的3D散点图，展示聚类结果
# 这里假设'age', 'bmi', 'charges'是DataFrame train中的列名，且'type'是聚类标签列
graph3dc(train, 'age', 'bmi', 'charges')

 

 

 

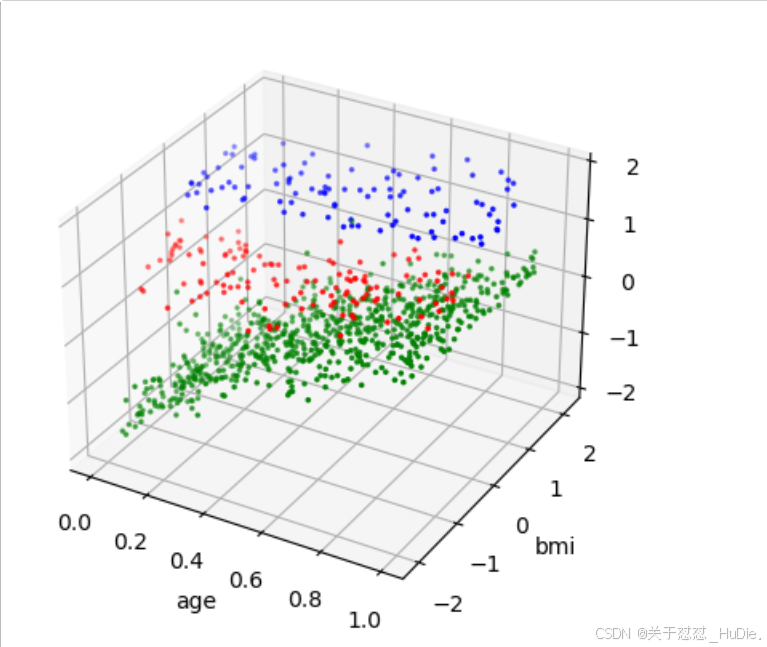
图6-5 聚类的结果

五、应用场景

DBSCAN算法的应用领域广泛，包括但不限于以下方面：

1. 地理信息系统（GIS）：在地理信息系统中，DBSCAN可以用来识别城市中的不同区域，比如根据人口密度识别住宅区、商业区等。

2. 图像处理：在图像分割中，DBSCAN可以基于像素点的密度将图像中的不同区域分离开来，用于目标检测和图像分割。

3. 生物信息学：在基因表达数据分析中，DBSCAN可以用来识别基因表达模式的聚类，帮助研究者发现基因之间的相似性。

4. 客户细分：在市场分析中，DBSCAN可以用于客户细分，根据购买行为和偏好将客户分为不同的群体。

5. 网络安全：在网络安全领域，DBSCAN可以用于异常检测，比如识别网络流量中的异常模式或潜在的恶意活动。

6. 天文学：在天文学中，DBSCAN用于星系的聚类分析，帮助天文学家根据星系的分布和密度发现星系团。

7. 传感器网络：在传感器网络中，DBSCAN可以用于数据融合和异常检测，比如根据传感器读数识别异常的环境变化。 DBSCAN算法的优势在于它不需要预先指定簇的数量，能够处理噪声数据，并且能够发现任意形状的簇。然而，DBSCAN算法对参数选择较为敏感，特别是邻域半径（eps）和最小点数（minPts）的选择，这需要根据具体应用场景进行调整。

六、拓展部分

DBSCAN、分层聚类和K均值聚类比较：

分层聚类（Hierarchical Clustering）：

原理：采用自底向上的方法，开始时将每个样本视为一个簇，然后逐步合并相近的簇，直到满足终止条件（如达到预设的簇数量或簇间的距离超过某个阈值）。
优点：能够生成一个具有层次结构的聚类树，便于观察和理解数据的聚类过程。同时，可以通过设置不同的终止条件来控制簇的数量和大小。
缺点：合并操作一旦完成就无法撤销，因此可能导致某些错误的合并。此外，当数据量较大时，计算复杂度较高，可能导致算法运行时间较长。

K均值聚类（K-Means Clustering）：

原理：通过迭代的方式将数据划分为K个簇，使得每个样本点与其所属簇的中心点之间的距离之和最小。算法的核心是不断更新簇的中心点，直到达到收敛条件。
优点：原理简单易懂，计算效率高，尤其适用于大规模数据集。同时，K均值聚类能够发现球状簇，对于某些特定形状的数据集具有较好的聚类效果。
缺点：需要提前设定簇的数量K，不同的K值可能导致不同的聚类结果。此外，K均值聚类对初始簇中心的选择敏感，可能导致局部最优解而非全局最优解。同时，对于非凸形状的簇或噪声数据，K均值聚类的效果可能不佳。

4. 与K-means算法的对比：
与K-means算法的对比：K-means算法需要预定义聚类数量，且不能处理噪声数据或非凸形状的聚类，而DBSCAN算法则可以处理这些问题。

 

 

对噪声的敏感度：

DBSCAN：能够识别并处理噪声（图中未分配到任何簇的点）。它通过设置邻域的大小（eps）和最小样本点数（min_samples）来定义一个簇。如果一个点的邻域内没有足够的点，它将被标记为噪声。
k-means：没有明确的噪声处理机制。每个点都会被分配到最近的簇中心，即使这个点可能是一个异常值。
簇的形状：

DBSCAN：可以识别任意形状的簇，因为它是基于密度的。这意味着即使簇的形状不规则，DBSCAN也能够识别出来。
k-means：倾向于识别大小相似的球状簇。这是因为k-means通过最小化每个点到簇中心的距离（通常是欧几里得距离）来形成簇。
簇的数量：

DBSCAN：不需要预先指定簇的数量。算法会根据数据的密度自动确定簇的数量。
k-means：需要预先指定簇的数量（k值）。这可能会导致对数据的误解，如果选择的k值与数据的实际簇数量不匹配。
对初始条件的敏感度：

DBSCAN：对初始条件（如选择的邻域大小和最小样本点数）敏感，但对初始簇中心的选择不敏感。
k-means：对初始簇中心的选择非常敏感，不同的初始条件可能导致不同的聚类结果。
计算复杂度：

DBSCAN：计算复杂度较高，尤其是在处理大规模数据集时，因为它需要计算数据集中每一对点的距离。
k-means：计算复杂度相对较低，因为它主要涉及距离计算和簇中心的更新。
总结来说，这三种聚类算法各有优缺点，适用于不同的数据集和场景。在选择聚类算法时，需要根据数据的特性、聚类的目的以及算法的性能要求进行综合考虑。例如，当数据集中存在噪声或异常值时，DBSCAN可能是一个更好的选择；当需要观察数据的层次结构时，分层聚类可能更合适；而当数据量较大且需要快速得到聚类结果时，K均值聚类可能是一个更高效的选择。
————————————————

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/2201_75552078/article/details/144334352