数据结构——有序向量的查找与改进

有序向量的查找

查找

• 接口：tempalte static Rank search(T* a,T const& e, Rank lo, Rank hi)
• 语义规定：在有序向量的区间[lo, hi)内，确定不大于e的最后一个节点的秩
• 复杂度：若采用最朴素的二分策略，那么每次都将问题规模缩小一半左右，这样经过至多\(log_2(hi-lo)\)次迭代，复杂度不超过\(O(logn)\)，而改进基本上是线性因子。
• 查找长度：查找算法执行元素大小比较操作的次数

虽然我们定义了一个通常会使用的语义，但是这里我们还是先分析几个安利，方便我们理解改进的方法
在前3个查找方法中，我们规定查找的语义为：在有序向量的区间[lo, hi)内，返回e的秩，若有多个相同值则返回最大的秩，若查询失败则返回-1

二分查找

原理：每次取lo与hi的终点，不停调整区间，经过至多两次比较可以完成一次迭代。
直到最后lo>=hi时(其实就是lo=hi)，此时的区间宽度为0，表示查询失败了。

// 二分查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( lo < hi ) { //每步迭代可能要做两次比较判断，有三个分支
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      if      ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
      else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
      else                  return mi; //在mi处命中
   } //成功查找可以提前终止
   return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

查询长度分析：
为了评定各个查询的细微差距，我们考察查询长度，同样有最好最坏和平均。
这里我们依旧考察平均查询长度:\(C_{average}(k)\)
设在长度为\(n=2^k-1\)的有序向量中进行查询

1、成功查询长度
递推基：
\(C_{average}(k)=C(1)=2\)
递推分析：对于成功查询，总共有三种情况
1.经过1次比较，问题转化为2^{k-1}-1的新问题;
2.经过2次比较，问题转化为2^{k-1}-1的新问题;
3.经过2次比较，在mid处命中，查询成功.
那么则有递推公式

\[C(k) = [C(k-1)+(2^{k-1}-1)] + 2 +[C(k-1)+2*(2^{k-1}-1)]=2*C(k-1)+3*2^{k+1}-1 \]

令

\[F(k)=C(k)-3k*2^{k-1}-1 \]

则有

\[F(1)=2;F(k)=2F(k-1)=2^2F(k-2)=\dots=2^{k-1}F(1)=-2^k \]

于是

\[C(k) = F(k)+3k*2^{k-1}+1=(\frac{3}{2}k-1)*(2^k-1)+ \frac{3}{2}k \]

进而得到

\[C_{average}=\frac{C(k)}{2^k-1}=\frac{3}{2}k-1+\frac{3}{2}k*\frac{1}{2^k-1}=\frac{3}{2}k-1+O(\varepsilon) \]

n趋于无穷时忽略末尾收敛的无穷小量平均查找长度为：

\[O(1.5k)=O(1.5\cdot log_{2}n) \]

2、失败查询长度
当查询失败时，则一定会在\(lo \ge hi\)时结束运行，那么运行时一定每次都经历了2次比较，与上方证明成功查询类似可证：查询失败的查找长度也为\(O(1.5\cdot log_{2}n)\)

Fibonacci查找

虽然上一节的二分查找已经把平均查找长度降到了\(O(1.5\cdot log_{2}n)\)，比遍历查询的方式快不少，但是仍有改进空间。

我们刚刚设计的二分查找算法看似是将数组平均分成两半，这看似是一种平衡的分割方式，但实际上由于进入两侧所需要的比较次数不同，因此其中蕴含着不平衡的因素。

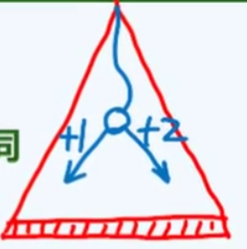
如图所示，在查找过程中，实际是向左侧查找成本更低，而右侧更高，因此我们得到了一个改进思路：将分割点向右侧移动，这样可以让低成本的操作执行次数更多，这对查找转向成本不平衡起到补偿作用。

在这里我们正好可以选择斐波那契数作为切分点，在这种策略下，这样切分的效率是最高的，这又一次展现出了黄金分割点的神奇。
假设向量长度为\(n=fib(k)-1\)，则令切分点为\(fib(k-1)-1\)

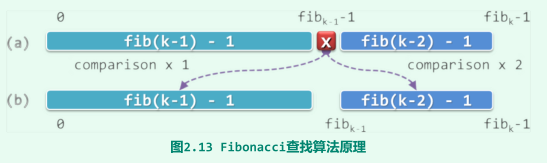
下面给出其查找长度的推导：
向量长度为\(n=fib(k)-1\)，假设平均成功查找长度为\(C_{average}(k)\)

可以有两条边界条件式

\[C_{average}(2)=C(2)=0;C_{average}(3)=C(3)=2 \]

递推公式为：

\[C(k)=[C(k-1)+(fib(k-1)-1)]+2+[C(k-2)+2*(fib(k-2)-1)] \]

令

\[F(k)=-C(k)+k*fib(k)+1 \]

化简得

\[C(k)=k*fib(k)-fib(k+2)+1=(k-\Phi^2)*fib(k)+1+O(\varepsilon) \]

其中，\(\Phi=\frac{\sqrt{5}+1}{2}=1.618\)
于是

\[C_{average}(k)=C(k)/(fib(k)-1)=k-\Phi^2+1+O(\varepsilon) \]

忽略末尾收敛的波动项，平均查找长度为：

\[O(k)=O(log_{\Phi}n)=O(1.44\cdot log_{2}n) \]

这个相比于朴素的二分查找，效率略有提高。

#include "fibonacci/Fib.h" //引入Fib数列类
// Fibonacci查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch ( T* S, T const& e, Rank lo, Rank hi ) {
    //用O(log_phi(n = hi - lo)时间创建Fib数列
   for ( Fib fib ( hi - lo ); lo < hi; ) {  //Fib数列制表备查；此后每步迭代仅一次比较、两个分支
      while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找（分摊O(1)）
      Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点
      if      ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
      else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
      else                  return mi; //在mi处命中
   } //成功查找可以提前终止
   return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；失败时，简单地返回-1，而不能指示失败的位置

class Fib { //Fibonacci数列类
private:
   int f, g; //f = fib(k - 1), g = fib(k)。均为int型，很快就会数值溢出
public:
   Fib ( int n ) //初始化为不小于n的最小Fibonacci项
   { f = 1; g = 0; while ( g < n ) next(); } //fib(-1), fib(0)，O(log_phi(n))时间
   int get()  { return g; } //获取当前Fibonacci项，O(1)时间
   int next() { g += f; f = g - f; return g; } //转至下一Fibonacci项，O(1)时间
   int prev() { f = g - f; g -= f; return g; } //转至上一Fibonacci项，O(1)时间
};

二分查找·改

在朴素的二分查找中，切分均等，但转向代价不均等；fibonacci查找用不均等切分补偿了转向代价的不均等。
那么我们可以换一种思路，也很容易想到，可以不可以使用一种专项条件均等的判断方式，使无论向左或向右，都只经历一次比较？答案是可以的。

我们现在采用这种转换策略：只进行一次判断
1）\(e<x\):则e必然存在左侧区间\(S[lo,mi)\)中
2）\(x<=e\):则e必然存在左侧区间\(S[mi,high)\)中
这个策略的正确性是显而易见的

我们分析这个策略可以发现，他对于每一次查找，都必须深入到最深处，也就是说无论是最好情况还是最坏情况，他的查找长度都是一样的。
相对于朴素的二分查找，这种查找的最坏情况会更好(从\(O(1.5log_2n)\)变为\(O(log_{2}n)\))，但最好情况会更坏（从\(O(1)\)变为\(O(log_{2}n)\)）。
假设\(n=2^k-1\)

\[C(k)=C(k-1)+2^{k}-1+1+C(k-1)=2*C(k-1)+2^k \]

解得通项公式为

\[C(k)=k2^k \implies C_{average}=C(k)/(2^k-1)=k+O(\varepsilon)=log_{2}(n+1)+O(\varepsilon) \]

n趋于无穷时去掉末尾收敛项

\[O(n)=log_{2}n \]

可以看到，前面的系数已经变为1了，这个策略的平均查找长度有了一些提升。

// 二分查找算法（版本B）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo < hi <= _size
template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断，有两个分支；成功查找不能提前终止
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      ( e < S[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)
   } //出口时hi = lo + 1，查找区间仅含一个元素A[lo]
   return e < S[lo] ? lo - 1 : lo; //返回位置，总是不超过e的最大者
} //有多个命中元素时，返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

 

二分查找·改二（符合原语语义）

刚才为了改进这个算法，我们研究了几种修改过语义的查找方法，而现在我们要实现最初所说的一个查找方法，但是这其实只需要对判断条件作出一点点修改，整体的策略是不变的，具体可以直接查看代码。

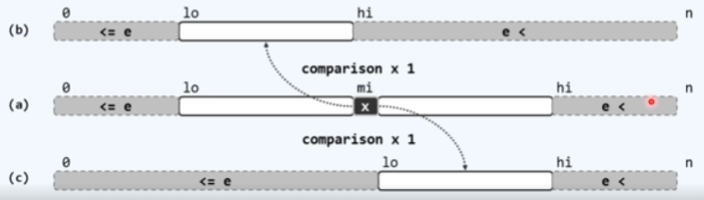
在如下代码中可以发现，我们查找的两个子区间分别是[lo, mi)和(mi, hi)，这中间的元素mi并未被包含入子区间，但这并不是一个纰漏，而是一个巧妙的设计，下面证明他的正确性：

不变性：A[0,lo) <= e < A[hi,n)
初始时：lo=0 & hi=n, A[0,lo) = A[hi,n) = \(\varnothing\) 自然成立
单调性：在这个策略中，深入的子区间分别是[lo, mi)和(mi, hi)，在各自区间内，仍严格满足不变性。

在算法执行的末尾，查询区间会被严格分割为两个部分（如下图所示），此时lo恰好指向<e的部分的头部，而lo-1则为我们要找的元素的秩。

template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( lo < hi ) { //每步迭代仅需做一次比较判断，有两个分支
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      ( e < S[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)
   } //成功查找不能提前终止
   return lo - 1; //循环结束时，lo为大于e的元素的最小秩，故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时，返回秩最大者；查找失败时，能够返回失败的位置

Fibonacci查找·改（符合原语语义）

#include "fibonacci/Fib.h" //引入Fib数列类
// Fibonacci查找算法（版本B）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   for( Fib fib ( hi - lo ); lo < hi;  ) { //Fib数列制表备查
      while( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找（分摊O(1)）
      Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点
      ( e < S[mi] ) ? hi = mi : lo = mi + 1; //比较后确定深入前半段[lo, mi)或后半段(mi, hi)
   } //成功查找不能提前终止
   return --lo; //循环结束时，lo为大于e的元素的最小秩，故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时，总能保证返回最秩最大者；查找失败时，能够返回失败的位置

参考资料

学堂在线——数据结构（上）2021秋（清华大学.邓俊辉）
课本、源码以及MOOC课程