数据结构——向量的扩充（分摊复杂度分析）

向量的扩充

不可扩充向量遇到的问题

在原本的向量中，由于采用静态空间管理策略：
开辟内部数组_elem[]并使用一段连续的物理空间
_capacity:总容量
_size:当前实际规模

 

这个管理策略显然存在不足，会发生上溢或者下溢
1、上溢（overflow）：_elem[]不足以存放所有元素
2、下溢（underflow）：_elem[]中元素寥寥无几
装填因子（load factor）：$ \lambda = _size/_capacity << 50% $

 

因此需要引入可扩充向量

可扩充向量

在可扩充向量中，我们可以对向量进行扩充（extendable vector）

 
我们采用如下的策略：
即将发生上溢的时候，适当的扩展向量的容量
即将发生上溢时，我们进行扩容。扩容时，开辟一个新的空间，然后将其内部的_elem指针指向这个新的空间，然后复制原本的内容到新的空间，最后释放原本的空间。
具体实现参考如下：

template <typename T> void Vector<T>::expand() { //向量空间丌足时扩容
 if ( _size < _capacity ) return; //尚未满员时，不必扩容
 if ( _capacity < DEFAULT_CAPACITY ) _capacity = DEFAULT_CAPACITY; //不低于最小容量
 T* oldElem = _elem; _elem = new T[_capacity <<= 1]; //容量加倍
 for ( int i = 0; i < _size; i++ )
 _elem[i] = oldElem[i]; //复制原向量内容（T为基本类型，或已重载赋值操作符'='）
 delete [] oldElem; //释放原空间
}

 

加倍扩容策略 vs 递增式扩容策略

上边的参考代码中展示了一种加倍扩容的策略，这一节将会分析这种策略的优势

递增式扩容策略

T* oldElem = _elem; _elem = new T[_capacity += INCREMENT];//追加固定大小的容量

最坏情况：在初始容量为0的空向量中，连续插入n = m*I >> 2个元素
于是在第1、I+1、2I+1、...次插入时，都需要扩容
即使不计申请空间操作，仅扩容过程中的复制，时间成本依次为\(0,I,2I,\dots,(m-1)I = O(n^2)//算术级数\)
每次扩容的\(\color{red}{分摊成本}\)为\(O(n)\)

 

加倍扩容策略

T* oldElem = _elem; _elem = new T[_capacity << 1]; //容量加倍

最坏情况：在初始容量为0的空向量中，连续插入n = 2^m >> 2个元素
于是在第1、2、4、8、16、...次插入时，都需要扩容
即使不计申请空间操作，仅扩容过程中的复制，时间成本依次为\(1,2,4,\dots,2^m = O(n)//几何级数\)
每次扩容的\(\color{red}{分摊成本}\)为\(O(1)\)

 

对比

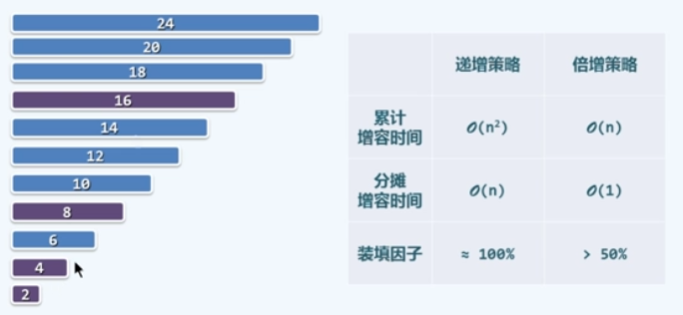
倍增策略是在空间上适当牺牲（但装填因子总不会小于50%），换取时间上的巨大收益。

 

平均时间复杂度 vs. 分摊时间复杂度