希尔排序

希尔排序

从插入排序改进

插入排序是一种常见的排序方式，他的最坏情况是\(O(n^2)\)，这对于一个排序算法来说效率相当低。我们要做的是改进插入排序，让他的时间复杂度降低。

为了实现这一目的，我们需要利用插入排序的特性：对于部分有序的序列，插入排序需要交换的次数很少，因此效率很高。

部分有序指数组中每个元素都距离自己的正确位置不远的情况。

先考虑插入排序，我们进行的操作是将每一个元素逐位进行移动，都是与相邻元素进行交换，这样对于需要移动很远的元素来说就会提高相当的时间复杂度。那么一个改进的思路就是：先将数组进行大致的排序，排序时可以进行远距离的移动。

要实现远距离移动，就必须有对应的方法，我们这里给出的方法就是对元素进行等间隔分组，将组中的元素进行排序。

假设分组间隔为\(h\)，且每个分组内有序，则称为h有序数组。我们多次进行分组排序，由于一开始h会很大，因此元素移动距离会相当远，这样就达到了我们远距离移动元素的目的，完成粗排序。

而后逐渐的减小\(H\)，这样排序也会越发精确。对于任何一个以1位结尾，的h序列，都能完成希尔排序，其原因是h=1时其实就是简单的插入排序。

经历这么多次的分组排序，时间复杂度如何呢？这个问题是一个难分析的问题，算法性能取决于\(h\)序列。不过可以确定的是，由于是先进行粗排，所以后续的插入排序的操作对象其实越发接近有序，这对于插入排序而言是非常友好的性质，效率会很高。因此，希尔排序虽然看上去增加了排序的次数，但是单次排序的用时却是不断下降的。

希尔排序的算法

1、选择一个h递增序列，并从h的最大值开始取
2、进行分组排序
3、减小h，重复步骤2，直至h=1

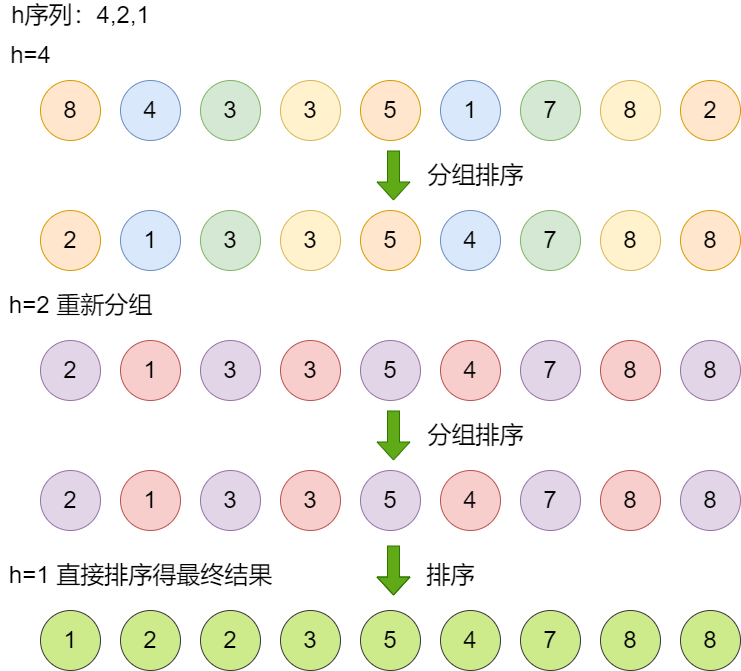
希尔排序的递增序列

希尔排序的递增序列（或者称增量序列）的选择是一个复杂的数学问题，其复杂度分析笔者现阶段难以完成，下面列举几个常用的递增序列，并不加证明的给出其应用在希尔排序中的时间复杂度

Shell 增量序列

\[h_t=\left \lfloor \frac{N}{2} \right \rfloor ,h_k=\left \lfloor \frac{h_{k+1}}{2} \right \rfloor \]

最坏时间复杂度为\(O(N^2)\)

Hibbard 增量序列

通项公式为：$$h_i=2^i-1$$
递推公式为：$$h_1=1,h_i=2*h_{i-1}+1$$
最坏时间复杂度为：\(O(N^{3/2})\)；平均时间复杂度为：\(\Theta(N^{5/4})\)

Knuth 增量序列

通项公式为：$$h_i=\frac{1}{2}(3^i-1)$$
递推公式为：$$h_1=1,h_i=3*h_{i-1}+1$$
最坏时间复杂度是\(O(n^{3/2})\)

使用Knuth增量序列的希尔排序实现

void shell_sort(int* start,int* end)
{
    int n=end-start;//获取数组长度
    int h=1;
    while(h<n) h=h*3+1;//生成增量序列
    while(h>=1)
    {
        //插入排序
        for(int i=h;i<n;i++)
        {
            for(int j=i;j>=h;j-=h)
            {
                if(start[j]<start[j-h])
                {
                    swap(start[j],start[j-h]);
                }
            }
        }
        //h减小
        h/=3;
    }
}