定点乘法原理
定点乘法原理
原码一位乘法
原码的一位乘与十进制计算乘法过程类似,只不过在存储方式上有一些技巧。因为两个n位乘数相乘得到的数应该是2n位,但是考虑到每对于乘数的每一位,我们读取并判断后都不会再使用,因此可以将其舍去;而恰好乘数部分需要一个新的位来进行位权的改变,因此我们可以利用乘数寄存器进行辅助存储。同时,移位操作也可以让判断电路固定在一个位置,有利于简化电路。
原码一位乘的具体过程如下图所示

可以看到,C就是乘数寄存器,而A称为部分积,最后计算完成后合并在一起,再补上符号位则得到原码的乘积
原码两位乘法
原码两位乘的原理也很简单,因为源码实际对于两位的情况只有4中并且不区分正负数,计算方法一致,如下表所示
| \(Y_{i+1}Y_i\) | 操作 | 部分积和乘数右移 |
|---|---|---|
| 00 | +0 | 1位 |
| 01 | +X | 1位 |
| 10 | +2X | 1位 |
| 11 | +3X | 1位 |
但是上表存在一个问题,他的行为中不变、+X、+2X(移位后加)都可以方便的通过一步完成,但是+3X则需要拆解成两步,如果拆解成两步,那么对硬件设计和程序执行效率都会产生严重的负面影响。
所以我们实际采用的方法是将+3X分解为+4X-X,这样的话就能解决这个问题了,因为+4X又可以通过左移两位快速实现。
现在的问题变为-X怎么处理,当即再做一次加法显然不合适,因此我们引入一个标志位C进行存储,C=1表示我们欠下一个+4X,这样下一次计算时计算机就会补上一个+4X。进行右移2位后,+4X就变成了+X,因此计算大大简化了。
那么我们就可以将操作表扩展成如下模式
| \(Y_{i+1}Y_i \ C\) | 部分积 | C置数 | 部分积和乘数右移 |
|---|---|---|---|
| 000 | +0 | \(0 \rightarrow C\) | 2位 |
| 001 | +X | \(0 \rightarrow C\) | 2位 |
| 010 | +X | \(0 \rightarrow C\) | 2位 |
| 011 | +2X | \(0 \rightarrow C\) | 2位 |
| 100 | +2X | \(0 \rightarrow C\) | 2位 |
| 101 | -X | \(1 \rightarrow C\) | 2位 |
| 110 | -X | \(1 \rightarrow C\) | 2位 |
| 111 | +0 | \(1 \rightarrow C\) | 2位 |
如果遇到奇数位乘法,最后一位按照一位乘处理。
最后给出一个例子:
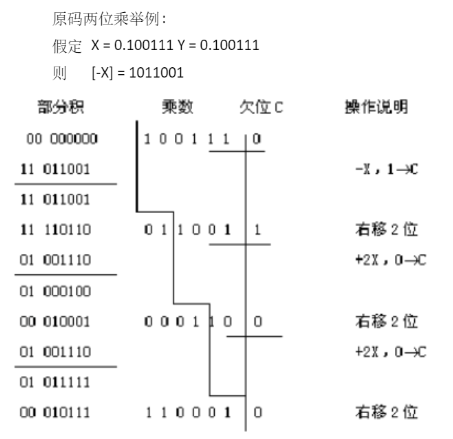
补码一位乘法
前置知识
补码的乘法我们选用纯小数作为推导的例子,因为纯小数具有一个非常优秀的性质:\([-X]_补=-[X]_补(mod\ 2)\)
证明:
对于纯小数,其补码转化为真值的公式为:\([X]_补 = 2 + X(mod\ 2)\)
在模2条件下,可以对数加上任意\(2^k\),因此\([-X]_补 = 2 - X (mod\ 2) = - (X + 2)(mod\ 2)=-[X]_补\)
矫正法
结论:$$[X \times Y]_补 = [X]_补 \times (0.Y_1 Y_2 \dots Y_n) + [-X]_补 \times Y_0$$
其中,\(Y_0\)为符号位
证明:
对于被乘数X而言,其实不影响运算,因为X始终作为加数而判断是否要加的是Y,因此只有Y的正负会影响计算方法。
(1)Y>0时,显然与原码乘法计算方法相同,公式的第二项为0
(2)Y<0时
假设
则
此时我们发现,Y被表示成了一个正数减去1的形式,那么
综上所述,得到\([X \times Y]_补 = [X]_补 \times (0.Y_1 Y_2 \dots Y_n) + [-X]_补 \times Y_0\)
booth公式
\( [X \times Y] = [X]_补 \times (0.Y_1 Y_2 \dots Y_n) + [-X]_补 \times Y_0\\ \ \ \ \ \ \ \ = [X]_补 \times (-Y_0 + 2^{-1} Y_1 + 2^{-2} Y_2 + \dots + 2^{-n} Y_n) \\ \ \ \ \ \ \ \ = [X]_补 \times (-Y_0 +(Y_1 - 2^{-1} Y_1) +(2^{-1} Y_2 - 2^{-2} Y_2) + \dots + ( 2^{-n+1} Y_{n} - 2^{-n} Y_n) \ \ ) \\ \ \ \ \ \ \ \ = [X]_补 \times (\ (Y_1-Y_0) + 2^{-1}(Y_2 - Y_1) + 2^{-2}(Y_3 - Y_2) + \dots + 2^{-n}(Y_{n+1} - Y_n) \ ) \\ \ \ \ \ \ \ \ 其中Y_{n+1} = 0 \)
拆解为递推公式则为
booth乘法运算按照:
(1)在乘数Y后附加一位,初始值\(Y_{n+1}=0\)
(2)每次运算后部分积和乘数均右移一位,操作由\(Y_{n-1}Y_n\)决定,且\(\color{red}{符号位参与运算}\)
| \(Y_{n-1} Y_{n}\) | 部分积 | 部分积和乘数右移 |
|---|---|---|
| 00 | +0 | 1位 |
| 01 | \(+[X]_补\) | 1位 |
| 10 | \(-[X]_补\) | 1位 |
| 11 | +0 | 1位 |
\(\color{red}{
注意:在进行运算的过程中因为符号位也参与运算,所以有可能出现溢出}\)\(\color{red}{现象,因此需要采用双符号位来进行计算,避免溢出错误}\)
例:1.00xxxx + 1.01xxxx的情况就会出现溢出错误,如果采用单个符号位,进行算术右移后会导致出错;此时应当采用11.00xxxx + 11.01xxxx保证符号位正常
补码两位乘法
与原码两位乘类似,补码两位乘也是同时进行两次乘法运算,设上次、第一次与第二次的部分积分别为\([Z]_补,[Z']_补,[Z'']_补\)
则
\(
[Z']_补 = 2^{-1}\{[Z]_补 + (Y_{i+1} - Y_i)[X]_补\} \\
[Z'']_补 = 2^{-1}\{[Z']_补 + (Y_{i} - Y_{i-1})[X]_补\} \\
[Z'']_补 = 2^{-1}\{ 2^{-1}\{[Z]_补 + (Y_{i+1} - Y_i)[X]_补\} + (Y_{i} - Y_{i-1})[X]_补\} \\
[Z'']_补 = 2^{-2}\{ [Z]_补 + (Y_{i+1}+Y_i-2Y_{i-1})[X]_补 \}
\)
由此可见两位乘由\(Y_{i+1},Y_i,Y_{i-1}\)三位共同决定操作
写成下表形式
| \(Y_{n-1} Y_{n} Y_{n+1}\) | 部分积运算 | 部分积和乘数右移 |
|---|---|---|
| 000 | +0 | 2位 |
| 001 | \(+[X]_补\) | 2位 |
| 010 | \(+[X]_补\) | 2位 |
| 011 | \(+2[X]_补\) | 2位 |
| 100 | \(-2[X]_补\) | 2位 |
| 101 | \(-[X]_补\) | 2位 |
| 110 | \(-[X]_补\) | 2位 |
| 111 | +0 | 2位 |
【!!!】关于补码两位乘特别需要注意符号位的处理和累加次数
- 部分积和被乘数的符号位设置为3位
- 乘数符号位分奇偶讨论
设n是乘数的数值部分的位数
(1)n为偶数

乘数符号位:2位
累加次数:\(\frac{n}{2} + 1\)
移位次数:\(\frac{n}{2}\)
(2)n为奇数
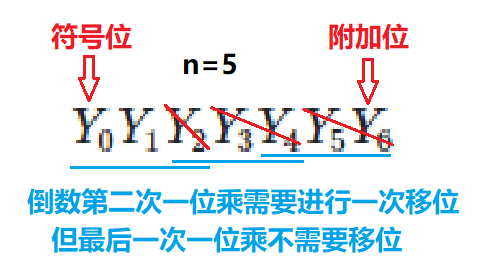
乘数符号位:1位
累加次数:\(\frac{n+1}{2}\)
移位次数:\(\frac{n+1}{2}\)(最后一次只移1位)
参考资料
https://wenku.baidu.com/view/b43fe4fd0242a8956bece412.html
https://blog.csdn.net/qq_42898299/article/details/118446418
https://blog.csdn.net/qq_45757722/article/details/111466747






 浙公网安备 33010602011771号
浙公网安备 33010602011771号