渐进时间复杂度

渐进时间复杂度

目录

• 渐进时间复杂度
  • \(T(n)\)
  • 三种渐进复杂度
  • 常用的时间复杂度
    • 高效解【很好】
      • 1.常数复杂度\(O(1)\)
      • 2.对数复杂度\(O(logn)\)
    • 有效解【可以接受】
      • 3.多项式复杂度$O(n^c)
    • 难解【难以接受】
      • 4.指数复杂度\(O(2^n)\)
  • 算法分析
    • 1.正确性分析
    • 2.复杂度分析
      • 主要工具
      • 级数
      • 循环
      • 封底估算

\(T(n)\)

\(T(n)\)是一个算法所需的基本操作的次数，通常是在RAM计算模型下的基本操作。

三种渐进复杂度

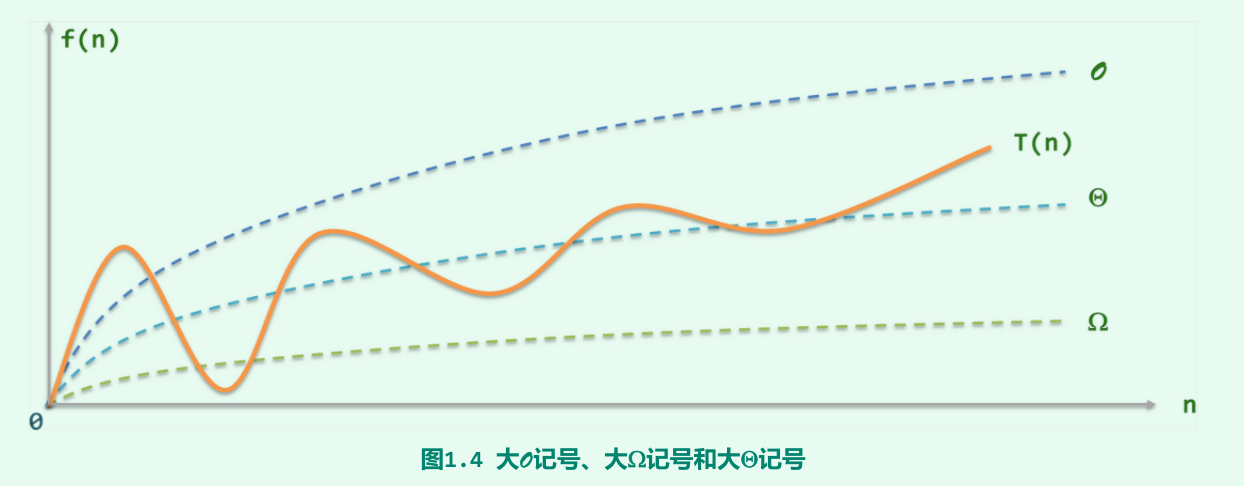
• 大\(O\)记号：最坏情况估计
  \(T(n) = O(f(n))\ \ iff\ \exist c>0,当n>>2后，有T(n)\color{red}{<}c\cdot f(n)\)
  例：\(\sqrt{5n\cdot [3n\cdot (n+2)+4]+6}<\sqrt{5n\cdot [6n^2+4]+6}<\sqrt{35n^3+6}<6\cdot n^{1.5}=O(n^{1.5})\)

  • 与\(T(n)相比，f(n)更为简洁，但是依然能反应前者的增长趋势\)
    • 常系数可以忽略：\(O(f(n))=O(c\dot f(n))\)
    • 低次项可以忽略：\(O(n^a+n^b)=O(n^a),a>b>0\)

• 大\(\Omega\)记号：最好情况估计
  \(T(n) = O(f(n))\ \ iff\ \exist c>0,当n>>2后，有T(n) \color{red}{>}c\cdot f(n)\)

• 大\(\Theta\)记号：准确估计
  \(T(n) = O(f(n))\ \ iff\ \exist c_1>c_2>0,当n>>2后，有c_1\cdot f(n) {>} T(n) {>}c_2\cdot f(n)\)

 
 

常用的时间复杂度

高效解【很好】

1.常数复杂度\(O(1)\)

\(a=b=2022=2022\cdot 2022 = O(1)\)

2.对数复杂度\(O(logn)\)

\( 常底数无所谓：\forall a,b>0,log_an=log_ab\cdot log_bn=\Theta(log_bn)\\ 常数次幂无所谓：\forall c>0,logn^c=c\cdot logn=\Theta(logn)\\ 对数多项式：123\cdot log^{123}n+log^{107}(n^2-n+1)=\Theta(log^{123}n)\\ 这类算法非常有效，时间复杂度趋于常数，复杂度低于任意多项式：\forall c>0,logn = O(n^c) \)

有效解【可以接受】

3.多项式复杂度$O(n^c)

\(a_{k}n^{k}+a_{k-1}n^{k-1}+\dots +a_1n+a_0=O(n^k)\)，低次项都可以忽略

难解【难以接受】

4.指数复杂度\(O(2^n)\)

\(T(n)=a^n\\ \forall c>1,n^c=O(2^n)，即任何多项式都被指数函数覆盖 \)
 
 
 

算法分析

\(算法分析的两个主要任务 = 正确性(不变性 \times 单调性) + 复杂度\)

1.正确性分析

不变性：每一次操作拥有的不变的性质

单调性：问题规模不断减少

2.复杂度分析

主要工具

• 迭代：级数求和
• 递归：递归跟踪 + 递归方程
• 猜想 + 验证

级数

• 算术级数

\[T(n)=1+2+\dots + n = n(n+1)/2=O(n^2) \]

• 幂方级数：比幂次高处一阶

\[\sum^n_{k=0} k^d \approx \int^n_0 x^{d}dx=\frac{1}{d+1} x^{d+1}|^n_0 = \frac{1}{d+1} n^{d+1} =O(n^{d+1})\\ T_2(n)=1^2+2^2+3^2+\dots +n^2 = O(n^3)\\ T_3(n)=1^3+2^3+3^3+\dots +n^3 = O(n^4)\\ T_4(n)=1^4+2^4+3^4+\dots +n^4 = O(n^5)\\ \dots \]

• 几何级数：(a>1) 与末项同阶

\[T_a(n) = a^0 + a^1 + \dots + a^n = \frac{a^{n+1}-1}{a-1} = O(a^n) \]

• 收敛级数：都是O(1)
  级数如果收敛那么其渐进复杂度就是\(O(1)\)
  e.g.几何分布$$(1-\lambda)[1\lambda +2\lambda^2 +3\lambda^3+ 4\lambda^4+ \dots ]=\frac{1}{1-\lambda}=O(1),0<\lambda<1$$
• 不收敛但是长度有限的级数
  • 调和级数
    \[h(n)=1+1/2+1/3+\dots +1/n = \Theta(logn) \]

  • 对数级数
    \[g(n)=log1+log2+\dots +logn=logn(n!)=\Theta(nlogn) \]

循环

循环与级数

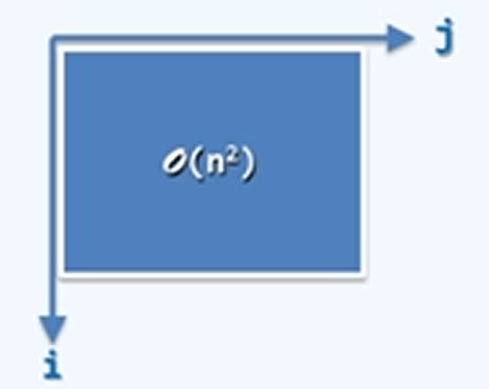
for(int i = 0; i < n; i++)
  for(int j = 0; j < n; j++)
    O(1)Operation(i,j);

\(T(n)=n+n+\dots +n=n*n=O(n^2)\)

 
2.

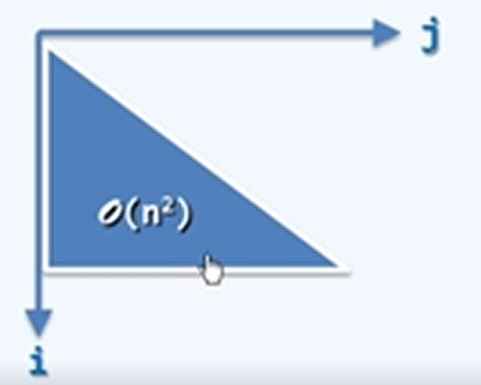
for(int i = 0; i < n; i++)
  for(int j = 0; j < i; j++)
    O(1)Operation(i,j);

\(T(n)=1+2+3+\dots +n=n*(n+1)/2=O(n^2)\)

 
3.

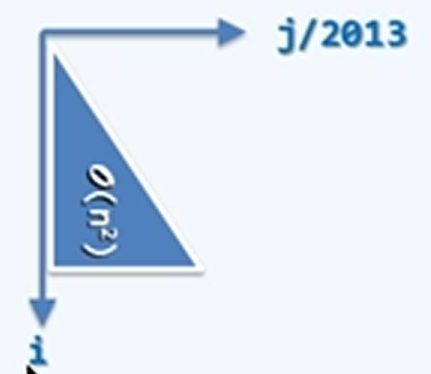
  for(int i = 0; i < n; i++)
    for(int j = 0; j < i; j+=2013)
      O(1)Operation(i,j);

\(T(n)=\dots\)仅仅是一个常系数优化

 
4.

  for(int i = 0; i < n; i <<= 1)
    for(int j = 0; j < i; j++)
      O(1)Operation(i,j);

\(T(n)=1+2+4+8+\dots+2^{\lfloor log_2(n-1) \rfloor} = 2^{\lceil log_2(n-1) \rceil} -1= O(n)\)

 
 

封底估算

时间估算

\[1天 \approx 10^5s\\ 100年 \approx 10^9s \]