《百面机器学习》拾贝----第三章:经典算法
不忘初心,方得始终.
01 支持向量机
支持向量机(Support Vector Machine,SVM)是众多监督学习方法中十分出色的一种,几乎所有讲述经典机器学习方法的教材都会介绍。关于SVM,流传着一个关于天使与魔鬼的故事。
以下关于SVM的介绍很生动:
传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球,如图3.1所示。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务,如图3.2所示。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如图3.3所示。

图3.1 分球问题1

图3.2 分球问题1的简单解

图3.3 分球问题2
SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远,如图3.4所示。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开,如图3.5所示。

图3.4 分球问题1的优化解

图3.5 分球问题1的优化解面对分球问题2
看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如图3.6所示。按照这种球的摆法,世界上貌似没有一根木棒可以将它们完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借念力抓起一张纸片,插在了两类球的中间,如图3.7所示。从魔鬼的角度看这些球,则像是被一条曲线完美的切开了,如图3.8所示。

图3.6 分球问题3
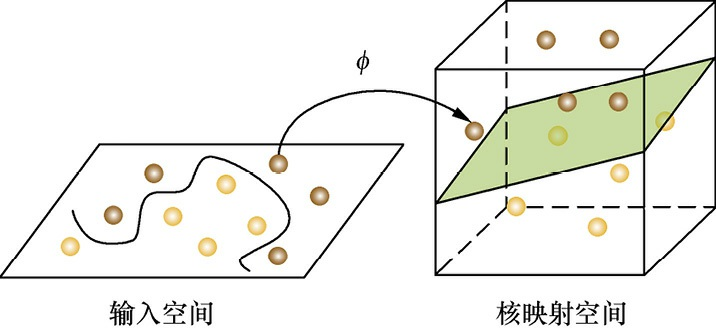
图3.7 高维空间中分球问题3的解

图3.8 魔鬼视角下分球问题3的解
后来,
“无聊”的科学家们把这些球称为“数据”;
把木棍称为“分类面”;
找到最大间隔的木棒位置的过程称为“优化”;
拍桌子让球飞到空中的念力叫做“核映射”;
在空中分隔球的纸片称为“分类超平面”。
——这,便是SVM的童话故事。
Q1:在空间上线性可分的两类点,分别向SVM分类的超平面上做投影,这些点在超平面上的投影仍然是线性可分的吗?
这个问题考察SVM模型推导的基础知识。
A1:
首先明确下题目中的概念,线性可分的两类点,即通过一个超平面可以将两类点完全分开,如图3.9所示。假设绿色的超平面(对于二维空间来说,分类超平面退化为一维直线)为SVM算法计算得出的分类面,那么两类点就被完全分开。我们想探讨的是:将这两类点向绿色平面上做投影,在分类直线上得到的黄棕两类投影点是否仍然线性可分,如图3.10所示。
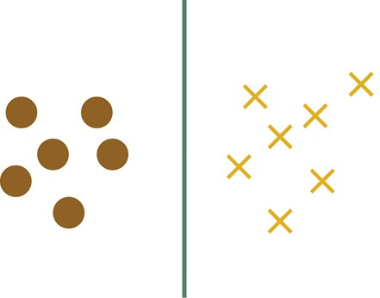
图3.9 支持向量机分类面
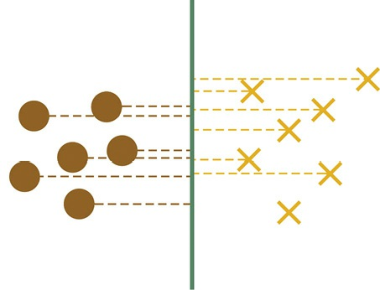
图3.10 样本点在分类面上投影
显然一眼望去,这些点在分类超平面(绿色直线)上相互间隔,并不是线性可分的。考虑一个更简单的反例,设想二维空间中只有两个样本点,每个点各属于一类的分类任务,此时SVM的分类超平面(直线)就是两个样本点连线的中垂线,两个点在分类面(直线)上的投影会落到这条直线上的同一个点,自然不是线性可分的。
但实际上,对于任意线性可分的两组点,它们在SVM分类的超平面上的投影都是线性不可分的。这听上去有些不可思议,我们不妨从二维情况进行讨论,再推广到高维空间中。
由于SVM的分类超平面仅由支持向量决定(之后会证明这一结论),我们可以考虑一个只含支持向量SVM模型场景。使用反证法来证明。假设存在一个SVM分类超平面使所有支持向量在该超平面上的投影依然线性可分,如图3.11所示。根据简单的初等几何知识不难发现,图中AB两点连线的中垂线所组成的超平面(绿色虚线)是相较于绿色实线超平面更优的解,这与之前假设绿色实线超平面为最优的解相矛盾。考虑最优解对应的绿色虚线,两组点经过投影后,并不是线性可分的。
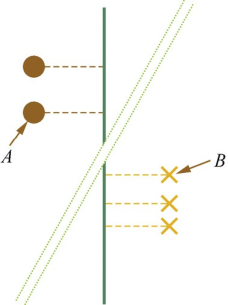
图3.11 更优的分类超平面
我们的证明目前还有不严谨之处,即我们假设了仅有支持向量的情况,会不会在超平面的变换过程中支持向量发生了改变,原先的非支持向量和支持向量发生了转化呢?下面我们证明SVM的分类结果仅依赖于支持向量。考虑SVM推导中的KKT条件要求。
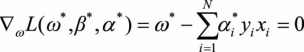 (3.1)
(3.1)
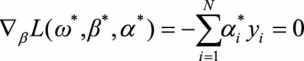 (3.2)
(3.2)
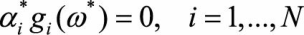 (3.3)
(3.3)
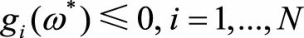 (3.4)
(3.4)
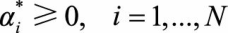 (3.5)
(3.5)
结合式(3.3)和式(3.4)两个条件不难发现,当 <0时,必有 ,将这一结果与拉格朗日对偶优化问题的公式相比较:
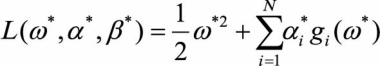 (3.6)
(3.6)
其中,
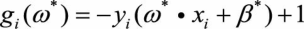 (3.7)
(3.7)
可以看到,除支持向量外,其他系数均为0,因此SVM的分类结果与仅使用支持向量的分类结果一致,说明SVM的分类结果仅依赖于支持向量,这也是SVM拥有极高运行效率的关键之一。于是,我们证明了对于任意线性可分的两组点,它们在SVM分类的超平面上的投影都是线性不可分的。
实际上,该问题也可以通过凸优化理论中的超平面分离定理(SeparatingHyperplane Theorem,SHT)更加轻巧地解决。该定理描述的是,对于不相交的两个凸集,存在一个超平面,将两个凸集分离。对于二维的情况,两个凸集间距离最短两点连线的中垂线就是一个将它们分离的超平面。
借助这个定理,我们可以先对线性可分的这两组点求各自的凸包。不难发现,SVM求得的超平面就是两个凸包上距离最短的两点连线的中垂线,也就是SHT定理二维情况中所阐释的分类超平面。根据凸包的性质容易知道,凸包上的点要么是样本点,要么处于两个样本点的连线上。因此,两个凸包间距离最短的两个点可以分为三种情况:两边的点均为样本点,如图3.12(a)所示;两边的点均在样本点的连线上,如图3.12(b)所示;一边的点为样本点,另一边的点在样本点的连线上,如图3.12(c)所示。从几何上分析即可知道,无论哪种情况两类点的投影均是线性不可分的。
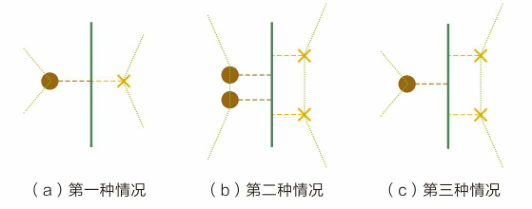
图3.12 两个凸包上距离最短的两个点对应的三种情况
至此,我们从SVM直观推导和凸优化理论两个角度揭示了题目的真相。其实,在机器学习中还有很多这样看上去显而易见,细究起来却不可思议的结论。面对每一个小问题,我们都应该从数学原理出发,细致耐心地推导,对一些看似显而易见的结论抱有一颗怀疑的心,才能不断探索,不断前进,一步步攀登机器学习的高峰。
Q2: 是否存在一组参数使SVM训练误差为0?
一个使用高斯核  训练的SVM中,试证明若给定训练集中不存在两个点在同一位置,则存在一组参数{α 1 ,...,α m ,b}以及参数γ使得该SVM的训练误差为0。
训练的SVM中,试证明若给定训练集中不存在两个点在同一位置,则存在一组参数{α 1 ,...,α m ,b}以及参数γ使得该SVM的训练误差为0。
A2:
根据SVM的原理,我们可以将SVM的预测公式写为:
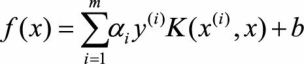 (3.8)
(3.8)
其中,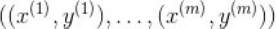 为训练样本,而{α 1 ,...,α m ,b}以及高斯核参数γ为训练样本的参数。由于不存在两个点在同一位置,因此对于任意的i≠j,有x(i)-x(j)>=
为训练样本,而{α 1 ,...,α m ,b}以及高斯核参数γ为训练样本的参数。由于不存在两个点在同一位置,因此对于任意的i≠j,有x(i)-x(j)>= ,我们可以对任意i,固定α i =1以及b=0,只保留参数γ,则有:
,我们可以对任意i,固定α i =1以及b=0,只保留参数γ,则有:
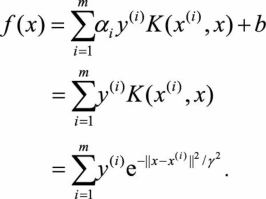
将任意x (j) 代入式(3.9)则有:
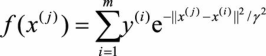 (3.10)
(3.10)
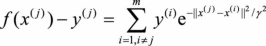 (3.11)
(3.11)
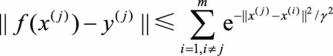 (3.12)
(3.12)
由题意知x(i)-x(j)>= ,取
,取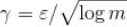 ,可将式(3.12)重写为:
,可将式(3.12)重写为:
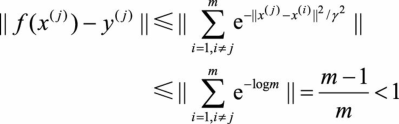 (3.13)
(3.13)

Q3:训练误差为0的SVM分类器一定存在吗?
A3:
虽然在问题2中我们找到了一组参数{α 1 ,...,α m ,b}以及γ使得SVM的训练误差为
0,但这组参数不一定是满足SVM条件的一个解。在实际训练一个不加入松弛变量
的SVM模型时,是否能保证得到的SVM分类器满足训练误差为0呢?

Q4:加入松弛变量的SVM的训练误差可以为0吗?
A4:

Q2-Q4侧重对核函数的理解。
02 逻辑回归
逻辑回归(Logistic Regression)可以说是机器学习领域最基础也是最常用的模型,逻辑回归的原理推导以及扩展应用几乎是算法工程师的必备技能。医生病理诊断、银行个人信用评估、邮箱分类垃圾邮件等,无不体现逻辑回归精巧而广泛的应用。
Q1: 逻辑回归相比于线性回归,有何异同?
A1:逻辑回归,乍一听名字似乎和数学中的线性回归问题异派同源,但其本质却是大相径庭。
首先,逻辑回归处理的是分类问题,线性回归处理的是回归问题,这是两者的最本质的区别。
逻辑回归中,因变量取值是一个二元分布,模型学习得出的是: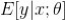
即给定自变量和超参数之后,得到因变量的期望,并基于此期望来处理预测分类问题。
而线性回归中实际上求解的是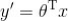 ,是对我们假设的真实关系
,是对我们假设的真实关系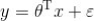 的一个近似,其中
的一个近似,其中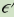 代表误差项,我们使用这个近似项来处理回归问题。
代表误差项,我们使用这个近似项来处理回归问题。
实际上,将逻辑回归的公式进行整理,我们可以得到: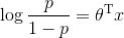 ,其中,
,其中,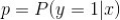
也就是将给定输入x预测为正样本的概率。
如果把一个事件的几率定义为该事件发生的概率与该事件不发生的概率的比值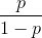 ,那么逻辑回归可以看作是对于“y=1|x”这一事件的对数几率的线性回归,于是“逻辑回归”这一称谓也就延续下来了。
,那么逻辑回归可以看作是对于“y=1|x”这一事件的对数几率的线性回归,于是“逻辑回归”这一称谓也就延续下来了。
在关于逻辑回归的讨论中,我们均认为y是因变量,而非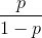 ,这便引出逻辑回归与线性回归最大的区别,即逻辑回归中的因变量为离散的,而线性回归中的因变量是连续的。并且在自变量x与超参数θ确定的情况下,逻辑回归可以看作广义线性模型(Generalized Linear Models)在因变量y服从二元分布时的一个特殊情况;而使用最小二乘法求解线性回归时,我们认为因变量y服从正态分布。
,这便引出逻辑回归与线性回归最大的区别,即逻辑回归中的因变量为离散的,而线性回归中的因变量是连续的。并且在自变量x与超参数θ确定的情况下,逻辑回归可以看作广义线性模型(Generalized Linear Models)在因变量y服从二元分布时的一个特殊情况;而使用最小二乘法求解线性回归时,我们认为因变量y服从正态分布。
当然逻辑回归和线性回归也不乏相同之处,首先我们可以认为二者都使用了极大似然估计来对训练样本进行建模。线性回归使用最小二乘法,实际上就是在自变量x与超参数θ确定,因变量y服从正态分布的假设下,使用极大似然估计的一个化简;而逻辑回归中通过对似然函数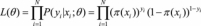 的学习,得到最佳参数θ。另外,二者在求解超参数的过程中,都可以使用梯度下降的方法,这也是监督学习中一个常见的相似之处。
的学习,得到最佳参数θ。另外,二者在求解超参数的过程中,都可以使用梯度下降的方法,这也是监督学习中一个常见的相似之处。
Q2: 当使用逻辑回归处理多标签的分类问题时,有哪些常见做法,分别应用于哪些场景,它们之间又有怎样的关系?
A2:
使用哪一种办法来处理多分类的问题取决于具体问题的定义。首先,如果一个样本只对应于一个标签,我们可以假设每个样本属于不同标签的概率服从于几何分布,使用多项逻辑回归(Softmax Regression)来进行分类:
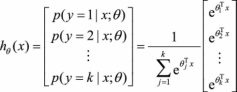
其中,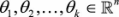 为模型参数,而
为模型参数,而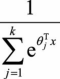 可以看作是对概率的归一化。
可以看作是对概率的归一化。
为了方便起见,将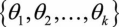 这k个列向量按顺序排列形成n×k维矩阵,写作θ,表示整个参数集。一般来说,多项逻辑回归具有参数冗余的特点,即将
这k个列向量按顺序排列形成n×k维矩阵,写作θ,表示整个参数集。一般来说,多项逻辑回归具有参数冗余的特点,即将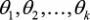 同时加减一个向量后预测结果不变。特别的,当类别数为2时:
同时加减一个向量后预测结果不变。特别的,当类别数为2时:
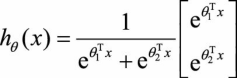
利用参数冗余的特点,我们将所有参数减去θ 1 ,上式变为:
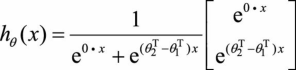
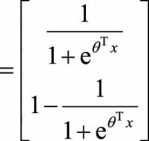
其中,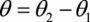 。而整理后的式子与逻辑回归一致。因此,多项逻辑回归实际上是二分类逻辑回归在多标签分类下的一种拓展。
。而整理后的式子与逻辑回归一致。因此,多项逻辑回归实际上是二分类逻辑回归在多标签分类下的一种拓展。
当存在样本可能属于多个标签的情况时,我们可以训练k个二分类的逻辑回归分类器。第i个分类器用以区分每个样本是否可以归为第i类,训练该分类器时,需要把标签重新整理为“第i类标签”与“非第i类标签”两类。通过这样的办法,我们就解决了每个样本可能拥有多个标签的情况。
03 决策树
决策树是一种自上而下,对样本数据进行树形分类的过程,由结点和有向边组成。结点分为内部结点和叶结点,其中每个内部结点表示一个特征或属性,叶结点表示类别。从顶部根结点开始,所有样本聚在一起。经过根结点的划分,样本被分到不同的子结点中。再根据子结点的特征进一步划分,直至所有样本都被归到某一个类别(即叶结点)中。
决策树作为最基础、最常见的有监督学习模型,常被用于分类问题和回归问题,在市场营销和生物医药等领域尤其受欢迎,主要因为树形结构与销售、诊断等场景下的决策过程十分相似。将决策树应用集成学习的思想可以得到随机森林、梯度提升决策树等模型。
一般而言,决策树的生成包含了特征选择、树的构造、树的剪枝三个过程。
Q1:决策树有哪些常用的启发函数?
A1:决策树的目标是从一组样本数据中,根据不同的特征和属性,建立一棵树形的分类结构。我们既希望它能拟合训练数据,达到良好的分类效果,同时又希望控制其复杂度,使得模型具有一定的泛化能力。
常用的决策树算法有ID3、C4.5、CART,它们构建树所使用的启发式函数各是什么?除了构建准则之外,它们之间的区别与联系是什么?
首先,我们回顾一下这几种决策树构造时使用的准则。
1、ID3——最大信息增益
2、C4.5——最大信息增益比
3、CART——最大 基尼指数
Q2:如何对决策树进行剪枝?
A2:决策树的剪枝通常有两种方法,预剪枝(Pre-Pruning)和后剪枝(Post-
Pruning)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号