【学习笔记】杨表

参考：

袁方舟《浅谈杨氏矩阵在信息学竞赛中的应用》

尺子姐姐的博客

wikipedia - Young tableau

声明：由于本人太菜等不可抗力因素，本文略过了很多部分的证明，重点在于介绍杨表的应用。如果想了解一些结论的证明，可以前往上面的链接。

如果有好题或者更多杨表的应用，欢迎补充！

杨表

杨图

杨图是一个有限的单元格集合，每一行左对齐，且每一行的长度从上到下不严格递减。

我们可以用一个集合 \(\lambda\) 表示一个杨图从上到下的每行单元格数量的集合，比如 \(\lambda = (5,4,1)\) 就长这样：

杨图的每个单元格 \((x,y)\) 有臂长、腿长、勾长：

臂长为这个单元格右面的单元格个数；
腿长为这个单元格下面的单元格个数；
勾长（即 hook/钩子的长，通常用 \(h_\lambda\) 表示）为这个单元格及其右面、下面的单元格总数，所以有 \(勾长=臂长+1+腿长\)。

杨表

杨表就是填充了内容的杨图。一般就是填正整数。

具体地，有：

严格杨表：满足每列数字严格递增、每行数字严格递增；
非严格杨表：满足每列数字严格递增、每行数字非严格递增；

建表

RSK 插入算法由 Robinson、Schensted、Knuth 提出，可将 \(k\) 插入杨表 \(S\) 中，算法流程如下：

移动到第一行。
在该行中找到 \(>k\) 的最小数 \(k'\)。
如果 \(k'\) 存在，将原本是 \(k'\) 的单元格替换为 \(k\)，然后令 \(k\gets k'\)，移动到下一行并重复步骤二。
否则，将 \(k\) 放到该行末尾。

容易证明在上述算法过后，\(S\) 仍然是半标准杨表。

容易使用 \(n\) 个 vector 维护以上过程，时间 \(\mathcal{O}(n^2\log n)\)。

考虑只维护前 \(\sqrt{n}\) 行、前 \(\sqrt{n}\) 列。前者直接在插入时大于 \(\sqrt{n}\) 时结束即可，后者考虑将序列翻转然后做同样的事情（定理，序列翻转，杨表也沿对角线翻折，可以用后面要讲的 LIS 问题理解；另外符号要换成大于等于，因为原杨表可能是半标准的）。

如此一来，可以用两个杨表拼起来以达到我们的需求，做到修改+查询 \(\mathcal{O}(n\sqrt{n}\log n)\)。

LIS 问题

若将排列 \(a_i\) 按 RSK 插入算法依次插入得到杨表 \(S\)，有性质：

第一行长度为 LIS 长度。
第一列长度为 LDS 长度。
前 \(k\) 行长度为最长的“LDS 长度不超过 \(k\)”的子序列长度。
前 \(k\) 列长度为最长的“LIS 长度不超过 \(k\)”的子序列长度。

注意，以上都只是长度，不代表杨表中的内容是一组 LIS/LDS。

如果不是排列，LIS 就变为了 LNDS（不上升）。

[CTSC2017] 最长上升子序列

离线之后，用结论直接转为求杨表前 \(k\) 列格数。因为题目要求序列（而不是排列） LIS，所以符号应为 >=。相应的，反杨表用 >。

用根号的 trick 维护，注意由于要实时维护前缀杨表，所以可以把翻转改成反转。时间复杂度 \(\mathcal{O}(n\sqrt{n}\log n)\)。

点击查看代码

// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define lnf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N = 5e4 + 5, B = 223, QQ = 2e5 + 5;
int n, Q, a[N], ans[QQ];
vector<pair<int, int> > q[N];
struct young
{
    vector<int> a[N];
    int op;
    int comp(int x, int y)
    {
        return x < y ? -1 : (x == y ? 0 : 1);
    }
    bool cmp(int x, int y)
    {
        return comp(x, y) >= op;
    }
    void insert(int i, int x)
    {
        if (i > B)
            return;
        if (a[i].empty() || !cmp(a[i].back(), x))
        {
            a[i].push_back(x);
            return;
        }
        int j = (op == 1 ? upper_bound(a[i].begin(), a[i].end(), x) : lower_bound(a[i].begin(), a[i].end(), x)) - a[i].begin();
        insert(i + 1, a[i][j]);
        a[i][j] = x;
    }
    void print(int i) // 调试用
    {
        if (a[i].empty())
            return;
        for (auto x : a[i])
            printf("%d ", x);
        puts("");
        print(i + 1);
    }
} s, t;

int main()
{
    cin >> n >> Q;
    for (int i = 1; i <= n; i++)
        scanf("%d", a + i);
    s.op = 0, t.op = 1;
    int m, k;
    for (int i = 1; i <= Q; i++)
        scanf("%d%d", &m, &k), q[m].push_back({k, i});
    for (int i = 1; i <= n; i++)
    {
        s.insert(1, a[i]), t.insert(1, -a[i]);
        for (auto j : q[i])
        {
            k = j.first;
            for (int l = 1; l <= min(B, k); l++)
                ans[j.second] += t.a[l].size();
            if (k > B)
                for (int l = 1; l <= B; l++)
                    if (s.a[l].size() > B)
                        ans[j.second] += min(k, int(s.a[l].size())) - B;
        }
    }
    for (int i = 1; i <= Q; i++)
        printf("%d\n", ans[i]);
    return 0;
}

钩子公式

其一

将一个排列填入一个形状为 \(\lambda\) 的标准杨表的种数为

\[f_\lambda = \frac{n!}{\prod h_\lambda(i,j)} \]

其中 \(h_\lambda\) 表示第 \(i\) 行第 \(j\) 列的格子的勾长。

有点难证，这里不证。

容易做到 \(O(n)\)，可参考例题P4484 的代码。

其二

将一个每个元素为 \(1\sim r\) 的正整数的序列填入一个形状为 \(\lambda\) 的半标准杨表的种数为

\[f_\lambda = \prod \frac{r+j-i}{h_\lambda(i,j)} \]

也可同理做到 \(O(n)\)。

如果要填入标准杨表，就把标准杨表第 \(i\) 列减去 \(i\)，转为填入 \(0\sim r-列数\) 的半标准杨表。

如果行之间也允许非严格递增（就叫 ta 半半标准杨表吧）的话也同理，考虑在半半标准杨表中第 \(i\) 行加上 \(i\) 之后转为 \(0\sim r+m\) 的半标准杨表。

Robinson-Schensted correspondence

\(1\) 到 \(n\) 的排列和一对内容为 \(1\) 到 \(n\) 排列并且形状相同的标准杨表 \((P,Q)\) 一一对应，即

\[n!=\sum_{\lambda\vdash n} f_\lambda^2 \]

其中 \(\lambda\vdash n\) 表示形状 \(\lambda=(\lambda_1,\lambda_2,...,\lambda_m)\) 为 \(n\) 的一个整数拆分。

P4484 [BJWC2018] 最长上升子序列

考虑排列与杨表对的双射，转化为枚举杨表对。此时 LIS 就是第一行长度，即 \(\lambda_1\)。答案就是

\[\frac{1}{n!}\sum_{\lambda\vdash n} f_\lambda^2 \lambda_1 \]

不考虑逆元的计算，时间复杂度 \(O(p(n)n)\)。

其中 \(p(n)\) 为 \(n\) 的整数拆分数，是亚指数级的。我打了一张 \(p(n)\) 的表：

n	p(n)
10	42
15	176
20	627
30	5604
50	204226
75	8118264
100	190569292
125	3163127352
150	40853235313
175	435157697830
200	3972999029388

因此通过此题绰绰有余，甚至可以跑过 \(n=50\)。

点击查看代码

// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define lnf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N = 35, MOD = 998244353;

inline int A(int x, int y) { return x + y >= MOD ? x + y - MOD : x + y; }
inline int S(int x, int y) { return A(x, MOD - y); }
inline int W(int x, int y) { return 1ll * x * y % MOD; }
inline int P(int x, int y) { int res = 1, t = x % MOD;
    while (y) { if (y & 1) res = W(res, t);
    t = W(t, t); y >>= 1; }
    return res; }
inline int D(int x, int y) { return W(x, P(y, MOD - 2)); }
inline int Q(int x) { return W(x, x); }

vector<int> lb;
int n, cnt[N], ans;

int f()
{
    memset(cnt, 0, sizeof(cnt));
    for (int i : lb)
        cnt[i]++;
    for (int i = n; i >= 1; i--)
        cnt[i] += cnt[i + 1];
    int res = 1;
    for (int i = 0; i < lb.size(); i++)
    {
        for (int j = 1; j <= lb[i]; j++)
            res = W(res, cnt[j] - i + lb[i] - j);
    }
    return D(1, res);
}

void dfs(int dep, int sum)
{
    if (dep == 1)
    {
        while (sum < n)
            lb.push_back(1), sum++;
        ans = A(ans, W(lb[0], Q(f())));
        while (!lb.empty() && lb.back() == 1)
            lb.pop_back();
        return;
    }
    for (; sum <= n; sum += dep, lb.push_back(dep))
        dfs(dep - 1, sum);
    while (!lb.empty() && lb.back() == dep)
        lb.pop_back();
}

int main()
{
    cin >> n;
    dfs(n, 0);
    for (int i = 1; i <= n; i++)
        ans = W(ans, i);
    cout << ans << endl;
    return 0;
}

一个 Trick

一个填入排列的杨表，如果从大往小删（直接删除，其余格子不变），不难发现每刻都是杨表。

考虑把原杨表的外轮廓表示出来，即从左下往右上走，向右走记为 1，向上走记为 0。则每次删除相当于交换一对相邻的 10。因此一个杨表的大小也等于外轮廓 0/1 序列的逆序对数。

应用：HackerRank - Triomio Tiling

菱形填充问题

先看一道经典的题：EntropyIncreaser 与菱形计数。

这个题非常良心的给了样例解释图，还上了色——很容易看出是一个~~学霸题~~墙角堆正方体状物。

于是考虑把这个立体图形拍扁成一个长方形，格子内是高度。

比如

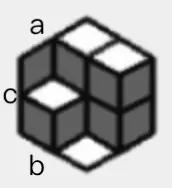
就可以转化为

2 2
1 0

然后就发现这是个 \(a\times b\) 半半标准杨表，填入的是 0~c 的数。那么第 \(i\) 行加上 \(i\)，转为 1~c+a 填入半标准杨表。

（为了方便思考，放一下半标准杨表钩子公式）

\[f_\lambda = \prod \frac{r+j-i}{h_\lambda(i,j)} \]

由于元素个数是 \(O(n^2)\)，所以朴素时间复杂度 \(O(n^2)\)。

把分母相同的放一起考虑，然后发现分子的积是一段连续奇数或偶数的积，预处理出来。时间复杂度优化到 \(O(n)\)（不算求逆元）。

点击查看代码

// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define lnf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N = 3e6 + 5, MOD = 998244353;
int pre[N];

inline int A(int x, int y) { return x + y >= MOD ? x + y - MOD : x + y; }
inline int S(int x, int y) { return A(x, MOD - y); }
inline int W(int x, int y) { return 1ll * x * y % MOD; }
inline int P(int x, int y) { int res = 1, t = x % MOD;
    while (y) { if (y & 1) res = W(res, t);
    t = W(t, t); y >>= 1; }
    return res; }
inline int D(int x, int y) { return W(x, P(y, MOD - 2)); }
inline int Q(int x) { return W(x, x); }

int prod(int l, int r)
{
    return D(pre[r], (l - 2 > 0 ? pre[l - 2] : 1));
}

int f(int n, int m, int r) // n <= m
{
    int ans = 1;
    for (int i = 1; i < n; i++)
    {
        ans = W(ans, D(prod(r - (i - 1), r + (i - 1)), P(n + m - i, i)));
        ans = W(ans, D(prod(r + m - n - (i - 1), r + m - n + (i - 1)), P(i, i)));
    }
    for (int i = n; i <= m; i++)
    {
        ans = W(ans, D(prod(r + i - 1 - 2 * (n - 1), r + i - 1), P(n + m - i, n)));
    }
    return ans;
}

int main()
{
    for (int i = 1; i <= 3e6; i++)
    {
        pre[i] = i;
        if (i > 2)
            pre[i] = W(pre[i], pre[i - 2]);
    }
    int a, b, c;
    cin >> a >> b >> c;
    if (a > b)
        swap(a, b);
    cout << f(a, b, c + a) << endl;
    return 0;
}

P8333 [ZJOI2022] 计算几何用到了这个技巧。

另外，这个问题其实还有另一种转换方式。

参考 Combinatorial Determinants

考虑在从原六边形的某一条边上出发，依次经过所处菱形的对边。

然后把横纵夹角变成 90 度，丢到坐标系里，就长这样：

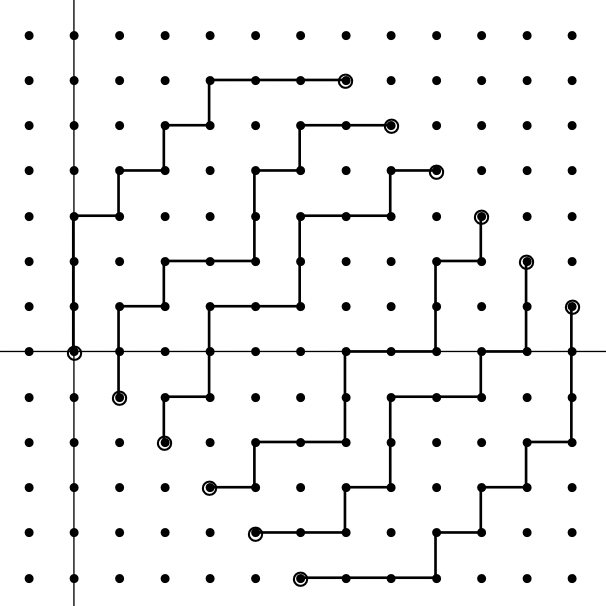
PPT 中用了 LGV 引理，但是我们可以用钩子公式来 \(O(n)\) 计算。

不过上面的图看起来很不顺眼呐。。。如果稍微压缩一下——

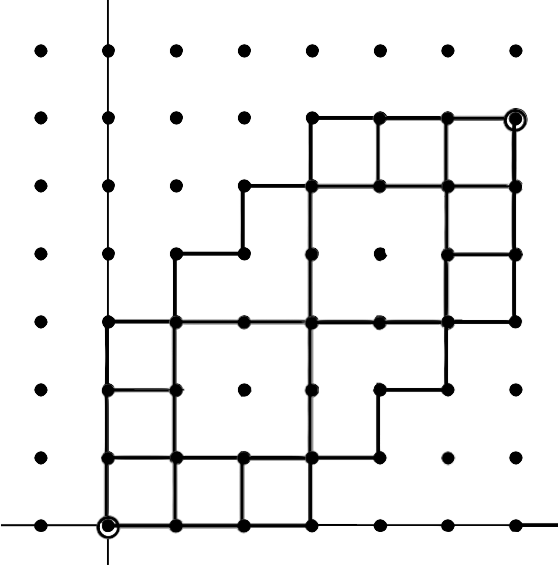
就变得很像杨表了（把起点合并了）。原图是几组不交的路径，压缩后就允许相交，不过不允许跨过。

显然，一个半半标准杨表的值小于等于某个数 \(k\) 的部分也一定是个杨表。所以上图相当于走 \(b\) 次不跨越上一次的路径，也相当于一个值域 \([0,b]\) 的半半标准杨表。染个色会更直观：

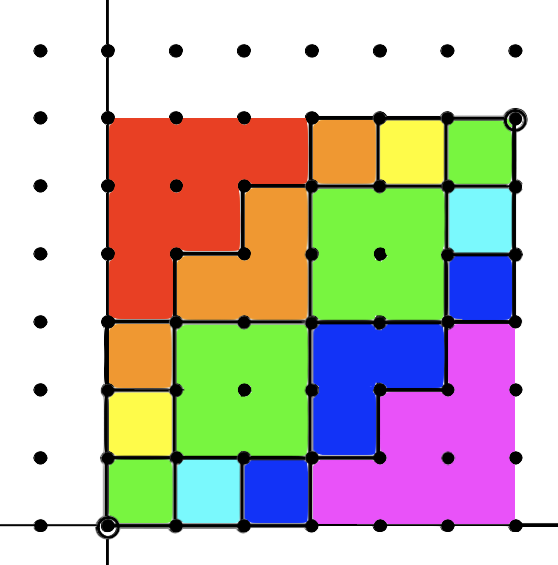
从红到粉是 0~b 的数。

于是问题就变成了，一个 \(c\times a\) 的半半标准杨表中填入 0~b 的方案数。跟之前的问题是一样的。

另一种网格上不交路径

参考袁方舟《浅谈杨氏矩阵在信息学竞赛中的应用》

平面直角坐标系上有一些点 \(\{(1,1),(1,2),...,(1,m)\}\) 和 \(\{(V,x_1),(V,x_2),...,(V,x_m)\}(x_i>i)\)，其中 \(V,x_i\) 是正整数。

一个方案为，从每个第一个集合的点 \((1,i)\) 出发走一条只往右或上的、终点为 \((V,x_i)\) 的路径，并且路径之间没有交点。

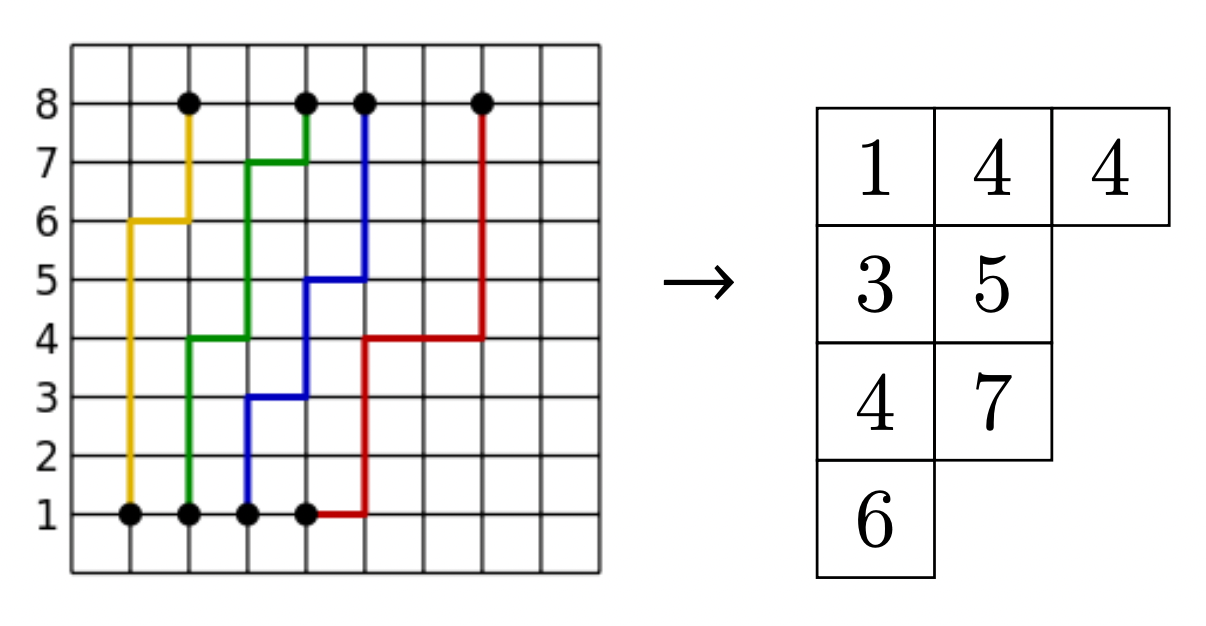
那么每一个方案可以和一张值域 \([1,V]\) 的半标准杨表一一对应。下面是一个例子：（懒得写转化方法了，下图应该能清晰体现）

n 维卡特兰数

参考袁方舟《浅谈杨氏矩阵在信息学竞赛中的应用》

一个经典的问题：从 \((0,0)\) 出发，不越过 \(x=y\)，每次横坐标或者纵坐标加 1，求到达 \((n,n)\) 的方案数。

大家都知道这是卡特兰数 \(C_n\)。不过其实也能转成杨表，而且不局限于到达 \((n,n)\)。

假设从 0 开始计时，每走一步是一个时间，考虑记下横坐标到达 \(i\) 的时间 \(X_i\)、纵坐标到达 \(i\) 的时间 \(Y_i\)。那么有：

\[\begin{cases} X_1<X_2<...<X_n\\ Y_1<Y_2<...<Y_n\\ X_i<Y_i \end{cases} \]

显然这是个 \(2\times n\) 的标准杨表，填入 \(1\sim2n\) 的排列。

用钩子公式计算出其填充方案数为 \(\frac{(2n)!}{n!(n+1)!}=\frac{1}{n+1}{2n\choose n}=C_n\)。

不难发现，这样一来终点就不一定要是 \((n,n)\)，如果是 \((n,m)(n\ge m)\) 的话，就是 \(\lambda=(n,m)\) 的、填入 \(1\sim n+m\) 排列。

此外，显然这个转化也适用于更高维：#6051. 「雅礼集训 2017 Day11」PATH。

\(\lambda=(a_0,a_1,...,a_{n-1})\) 的标准杨表填入 \(1\sim \sum a_i\) 排列。

那题需要再推一下式子然后 fft 优化一下。

以上就是我认为比较实用的内容了。

除了以上内容，杨表还有很多应用。IOI 论文里也有一些例题。

posted @ 2025-05-03 21:32 Aquizahv 阅读(65) 评论(0) 收藏举报

刷新页面返回顶部

Aquizahv's Blog

Follow this journey, to the stars.

【学习笔记】杨表

杨表

杨图

杨表

建表

LIS 问题

[CTSC2017] 最长上升子序列

钩子公式

其一

其二

Robinson-Schensted correspondence

P4484 [BJWC2018] 最长上升子序列

一个 Trick

菱形填充问题

另一种网格上不交路径

n 维卡特兰数

公告