【学习笔记】wqs二分

其实写这个主要是想解释一下它的原理，教程、习题什么的网上都有，比如这个。

就拿这题来讲吧。

首先我们画出一个函数 \(f(x)\) 表示 \(s\) 的度恰好为 \(x\) 时，最小生成树的权值和。

当然，这个函数只会取在某一些整点上，我们把它连起来就行了。

然后你会发现它是下凸的（凹的）。（证明不太会，在这里致歉，但我觉得这个记住就好了。另外我觉得上面博客链接的证明也是有点问题的。）

一个例子：

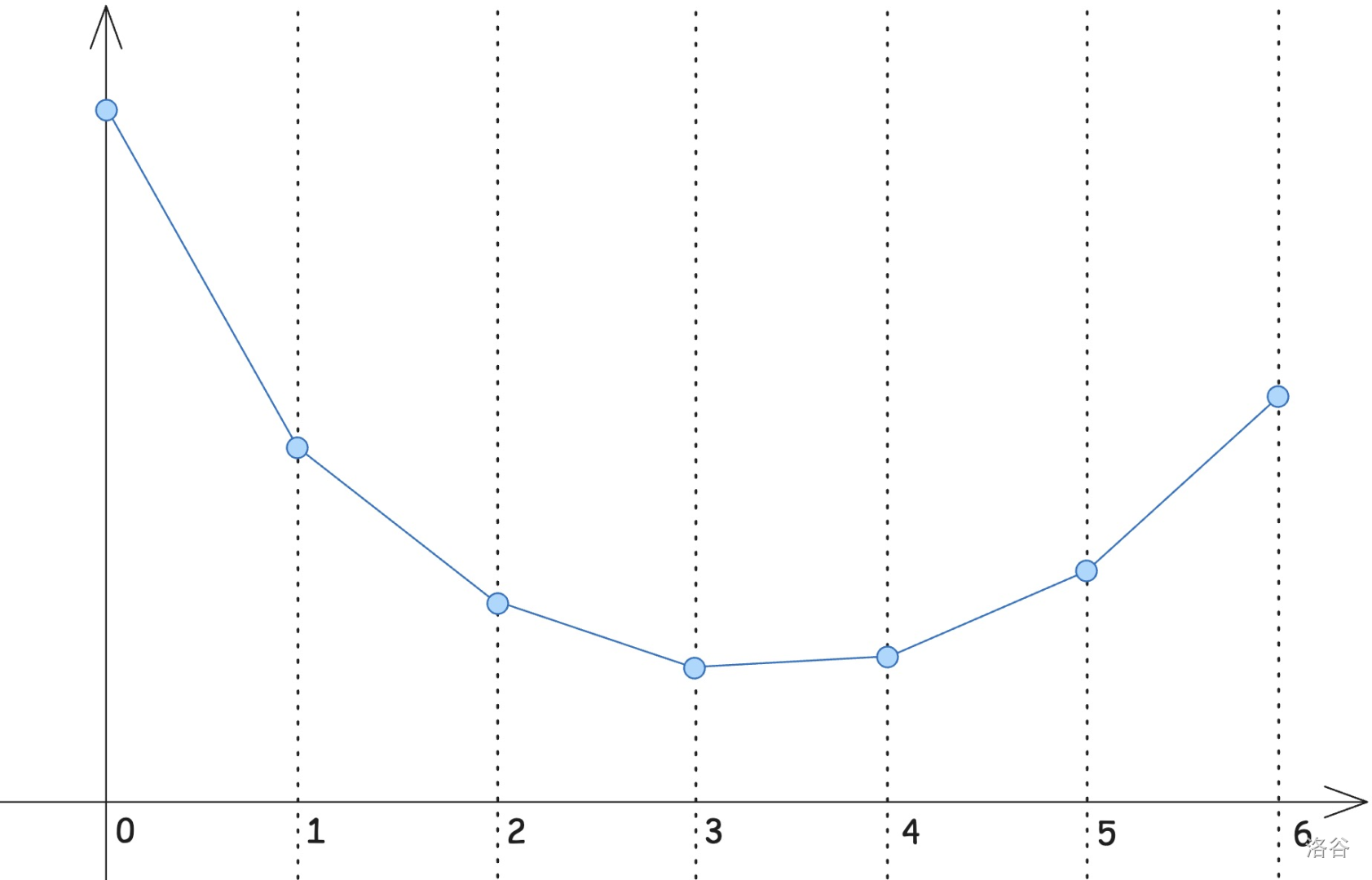
因为它是下凸的，所以两点之间的斜率是从左往右递增的。wqs二分的思想就是二分这个斜率，然后就能找到需要的 \(x\)，比如这道题就要求度恰好为多少。

那这个题要怎么实现呢？我们先随便找一个斜率 \(k\) 试试吧：

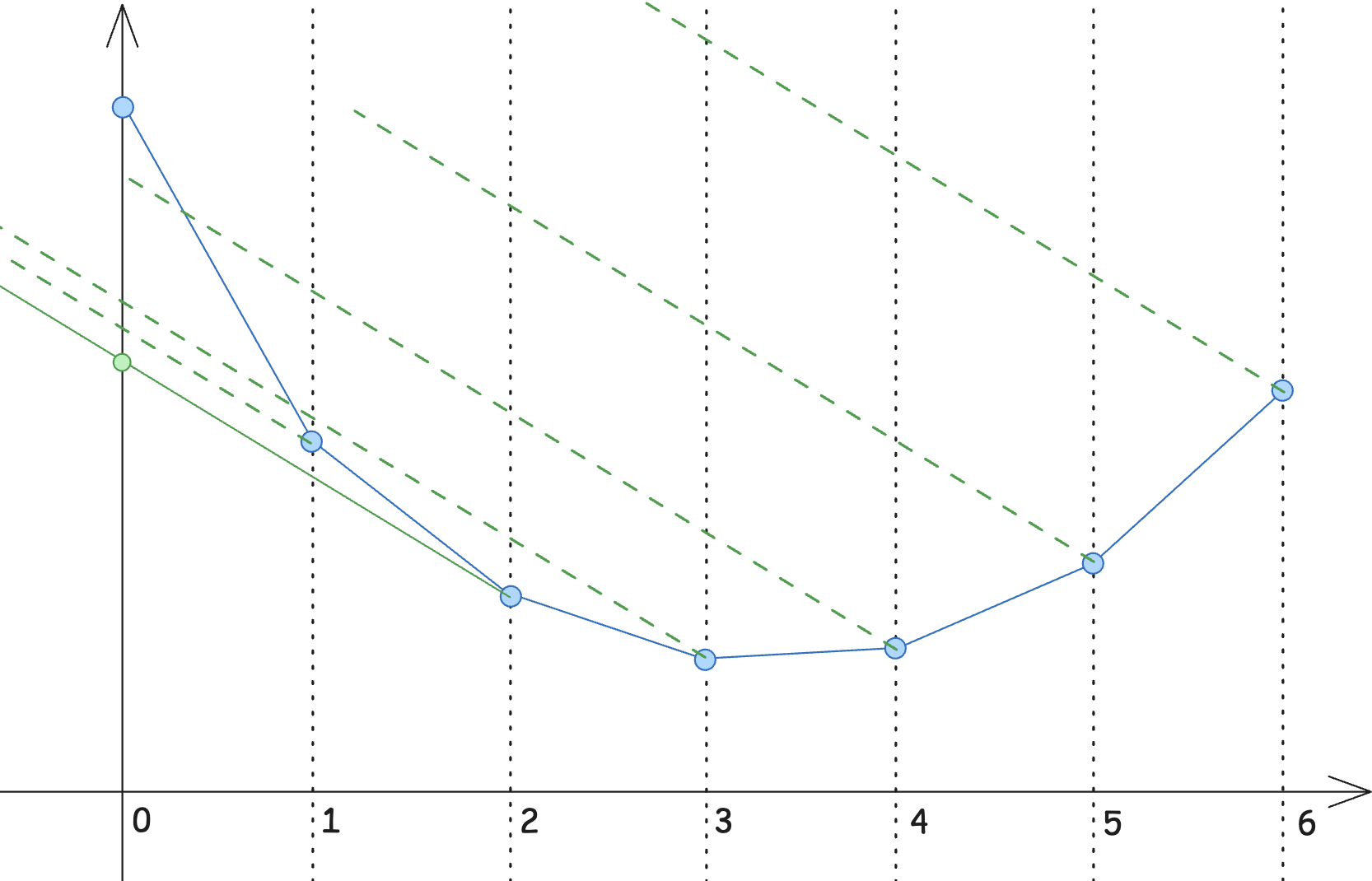
然后我们发现那个与 \(y\) 轴交点最低的直线所属的点就是这个斜率属于的 \(x\)。

设过 \(x\) 位置的点的直线交 \(y\) 轴与 \((0,b_x)\)，则有 \(f(x)=kx+b_x\)，即 \(b_x=f(x)-kx\)。

因为要最小化 \(b_x\)，所以要求 \(min\{f(x)-kx\}\) 的 \(x\)。

然后发现这个东西是可以构造的！考虑一个 \(s\) 的度为 \(x\) 的方案，那么我们只要让与 \(s\) 相连的边都加上 \(-k\) 就是 \(b_x\)！

因此，想要找到最小的 \(f(x)-kx\)，只需给所有与 \(s\) 相连的边加上 \(-k\)，跑一遍 mst，最后看有几个与 \(s\) 相连的边。

还有一些细节：

1. 要考虑 \(k\) 为小数的情况吗？当然不用，只要指定当边权相同时优先选与 \(s\) 相连的边就能达到同样的效果。
2. 如果出现三点共线，并且所求在其中一个怎么办？那么这几个点的 \(b_x\) 也一样，所以没有任何影响。不过要注意斜率，由于边权相等优先选与 \(s\) 相连的，所以二分的时候只要 mst 中 \(s\) 的度大于等于目标就算合法。

二分斜率是 \(\mathcal{O}(\log w)\) 的，\(w\) 是边权范围。用 Kruskal 求 mst 是 \(\mathcal{O}(m\log m + m\alpha(m))\) 的。但是实际上不用重新排序，可以用双指针把 \(\log\) 去掉。

所以总的是 \(\mathcal{O}(m\alpha(m)\log w)\)。

// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e4 + 5, M = 5e5 + 5;
int n, m, s, target;
int pos0, pos1;
struct Edge
{
    int u, v, w;
    bool operator<(const Edge t) const
    {
        return w < t.w;
    }
} e0[M], e1[M];

struct disjoint_set
{
    int f[N];
    void init(int lmt)
    {
        for (int i = 1; i <= lmt; i++)
            f[i] = i;
    }
    int find(int idx)
    {
        if (idx == f[idx])
            return idx;
        return f[idx] = find(f[idx]);
    }
    bool merge(int u, int v) // u -> v
    {
        int x = find(u), y = find(v);
        if (x != y)
        {
            f[x] = y;
            return true;
        }
        return false;
    }
} ds;

int cal(int mid, bool type)
{
    int i = 1, j = 1, res = 0, sum = 0, cnt = 0;
    ds.init(n);
    while (i <= pos0 || j <= pos1)
    {
        if (j > pos1 || (i <= pos0 && e0[i].w + mid <= e1[j].w)) // important: <=
        {
            if (ds.merge(e0[i].u, e0[i].v))
                sum += e0[i].w + mid, res++, cnt++;
            i++;
        }
        else
        {
            if (ds.merge(e1[j].u, e1[j].v))
                sum += e1[j].w, cnt++;
            j++;
        }
    }
    return type ? sum : (cnt == n - 1 ? res : -1); // b_x = sum
}

int main()
{
    cin >> n >> m >> s >> target;
    int u, v, w;
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &w);
        if (u == s || v == s)
            e0[++pos0] = {u, v, w};
        else
            e1[++pos1] = {u, v, w};
    }
    int tmp = cal(30001, 0); // s 的度最少要是多少
    if (tmp == -1 || tmp > target || pos0 < target)
    {
        puts("Impossible");
        return 0;
    }
    sort(e0 + 1, e0 + pos0 + 1);
    sort(e1 + 1, e1 + pos1 + 1);
    int l = -30001, r = 30001, res = 0;
    while (l <= r)
    {
        int mid = (l + r) >> 1;
        if (cal(mid, 0) >= target) // important: >=
        {
            res = mid;
            l = mid + 1;
        }
        else
            r = mid - 1;
    }
    cout << cal(res, 1) - target * res << endl;
    return 0;
}