【学习笔记】字符串全家桶

本文正在不定期更新。

期末考试前学了下这些东西，感觉很简单，不像某 mp。

然而期末 Day1 考完就忘了，所以还是写篇笔记吧。

前置知识：字典树、自动机。

AC自动机（ACAM）

先来看一下洛谷上的 AC 自动机模版题。

P5357 【模板】AC 自动机

给你一个文本串 \(S\) 和 \(n\) 个模式串 \(T_{1\sim n}\)，请你分别求出每个模式串 \(T_i\) 在 \(S\) 中出现的次数。

首先，AC 自动机的核心思想是：求 \(S\) 中有多少个模式串，相当于拿每个前缀找有多少个后缀是模式串。

这句话很显然，但他就是核心思想。

然后就来看看 AC 自动机如何处理这一过程：

举个例子，文本串：

abaaaba

模式串：

aa
ab
aba
ba

首先把模式串扔到字典树上。蓝色的加表示模式串中有“根到该节点的串”（下文称“根到一个节点的串”为该节点的串）。

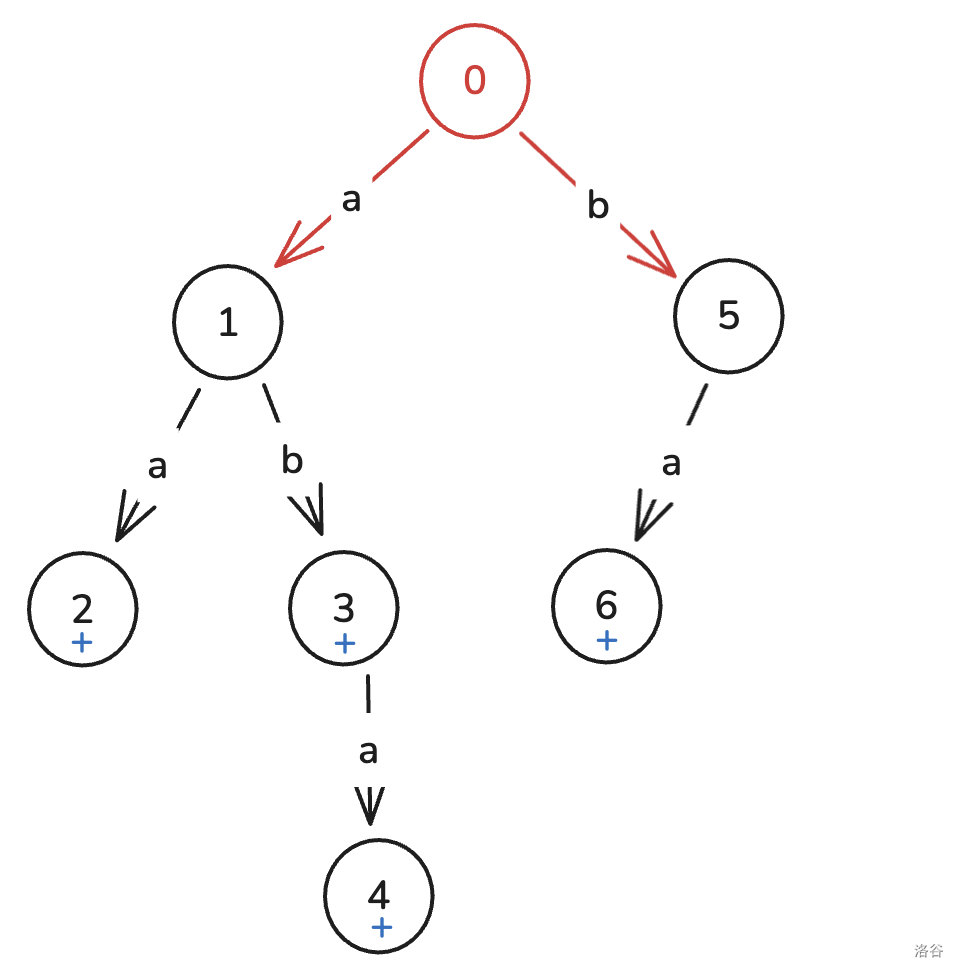
然后把 \(S\) 拿出来，从第一位开始在字典树上遍历，然后找该前缀的后缀去匹配：

一开始在根节点（红色的）。

  1. a，走到 \(\color{red}1\)。没有可以匹配的。

  2. b，走到 \(\color{red}3\)。显然有 ab。

  3. a，走到 \(\color{red}4\)。显然有 aba，但是此时 a ba 也行。然后我们发现他们是成一个后缀关系的！

aba
 ba
  a

现在无非就是求这个模式串有几个模式串是它的后缀。这个可以离线处理，等会儿再讲。

所以直接在当前点打个 \(\color{red}+1\) 的标记就好了（所以标红的数字就是打了标记）。

  1. a，由于 \(4\) 后面不能接 a 了，所以找其最长后缀，即 ba，跳到 \(6\) 节点。不过还是不能接。同理再找最长后缀 a，跳到 \(1\)，然后发现可以接，就走到 \(\color{red}2\)。这样最终的节点的串一定会是当前前缀（这里就是 abaa）的最长的后缀。这个过程是 AC 自动机的精髓，请务必理解。

fail

上面那些东西怎么实现？首先假设用来存 trie 的数组是 \(trie_{u,c}\)，表示节点 \(u\) 往后接字符 \(c\) 到的节点是多少（如果不能接就是空）；然后我们引入一个数组 \(fail_u\)，表示节点 \(u\) 的串的最长后缀所对的节点，并且这个后缀得在字典树上存在。比如说 \(fail_4 = 6,fail_6 = fail_2 = 1\)。至于如何求出所有的 \(fail\)，考虑当前节点 \(u\) 后接某个字符 \(c\)，走到儿子 \(v\)，那么可以尝试用 \(trie_{{fail_u},c}\) 更新 \(fail_v\)；如果 \(fail_u\) 接不了 \(c\)，继续尝试用 \(fail_{fail_u}\)，以此类推。

然后匹配的过程也差不多，可以参照步骤 \(4\)。我们算一下时间复杂度：最坏情况下，处理 \(fail\) 的过程是 \(\mathcal{O}(\sum(|T_i|)^2)\)，匹配过程是 \(\mathcal{O}(|S|)\) 的（类似双指针）。

处理过程太慢了！怎么优化？

优化！

以下是思考过程，如果赶时间只想看结果可以跳过。

再看看这个过程：

  1. 找到当前点的 \(fail\)，看看能否更新待更新点。

  2. 如果不能，用当前点的 \(fail\) 继续找，回到 1；否则就找到了。

是一个类似递归的过程。说的明白些：如果两个串有共同的 \(fail\)，他们的结果也会一样。

于是考虑记忆化！设 \(f(u,c)\) 表示 \(u\) 的串后面无法接 \(c\)（不在字典树上），它接了 \(c\) 之后的最长后缀是那个节点。

那直接有 \(f(u,c)=\begin{cases}trie_{fail_u,c} &(fail_u\ 之后能接\ c) \\f(fail_u,c) &(fail_u\ 之后不能接\ c)\end{cases}\)。注意边界是 \(f(root,c)=root\)。

然后把它记忆化一下就行。不过不用这么多数组，验证发现 \(f\) 和 \(trie\) 完全可以合并。

新 trie

于是最终就有了这样的形式：

本来的 trie 数组，如果不能接就是空。现在，我们修改一下它的定义：

\[trie_{u,c}=\begin{cases} trie_{u,c}（不变）&(节点\ u\ 之后能接\ c)\\ trie_{fail_{u},c}&(节点\ u\ 之后接不了\ c，且\ u\ 不为\ root（即空串）)\\ root&(节点\ u\ 之后接不了\ c，且\ u\ 为\ root) \end{cases} \]

（因此定义也可以说成是 \(u\) 的串后面接 \(c\) 之后的新串的 \(fail\)。）

这样以来，更新 \(fail_v\) 的时候直接用 \(trie_{fail_u,c}\) 就行。然后就解决。。。慢！还有一个问题：以什么顺序更新？

一个显然正确的办法就是 bfs，因为跳 \(fail\) 只会变短。好了，现在问题就完美解决了！而且代码甚至更短。此外，匹配过程也可以直接跳 \(trie_{u,c}\) 而不用去挨个找 \(fail\) 了，毕竟这俩几乎一个写法。

在上面例子中，以下是部分的新 \(trie\) 值：

\[\begin{aligned} trie_{6,a}=2\\ trie_{4,a}=2\\ trie_{2,a}=2\\ trie_{2,b}=3 \end{aligned} \]

代码实现

然后代码就是完全按照上面的过程写的：

void init_fail()
{
    queue<int> q;
    q.push(root);
    fail[root] = root;
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++)
        {
            if (!trie[u][i])
                trie[u][i] = u == root ? root : trie[fail[u]][i]; // 更新接不了的 trie（情况 2，3）
            else
            {
                fail[trie[u][i]] = u == root ? root : trie[fail[u]][i]; // 更新 fail，注意这里也要特判！
                q.push(trie[u][i]);
            }
        }
    }
}

匹配过程的函数你也一定会写了：

void Pair()
{
    int pos = strlen(s + 1);
    int u = root;
    for (int i = 1; i <= pos; i++)
    {
        u = trie[u][s[i] - 'a'];
        tag[u]++;
    }
}

现在你已经基本掌握 AC 自动机了！让我们回到洛谷的那个经典问题。

咱们继续匹配：

  1. a，\(2\) 接不了，就跳到 \(1\)，然后继续走到 \(\color{red}2\)。

  2. b，\(2\) 接不了，跳到 \(1\)，走到 \(\color{red}3\)。

  3. a，走到 \(\color{red}4\)。结束。

最后，树上的标记就是酱紫的：

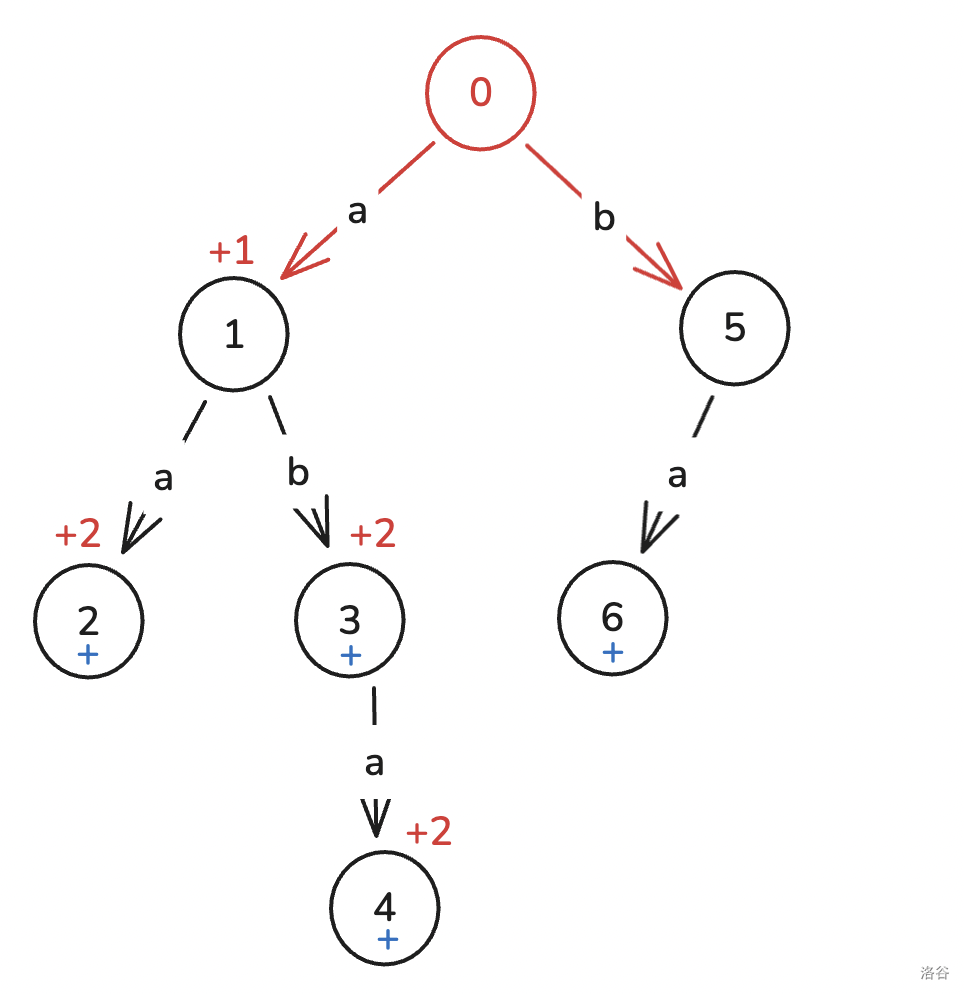
然后回到之前遗留的问题：计算模式串的出现次数。

遗留的问题

我们打上的标记，代表这个串的所有后缀都匹配上了。因此一个模式串的贡献，就是一棵 “fail 树” 的子树和。看图：

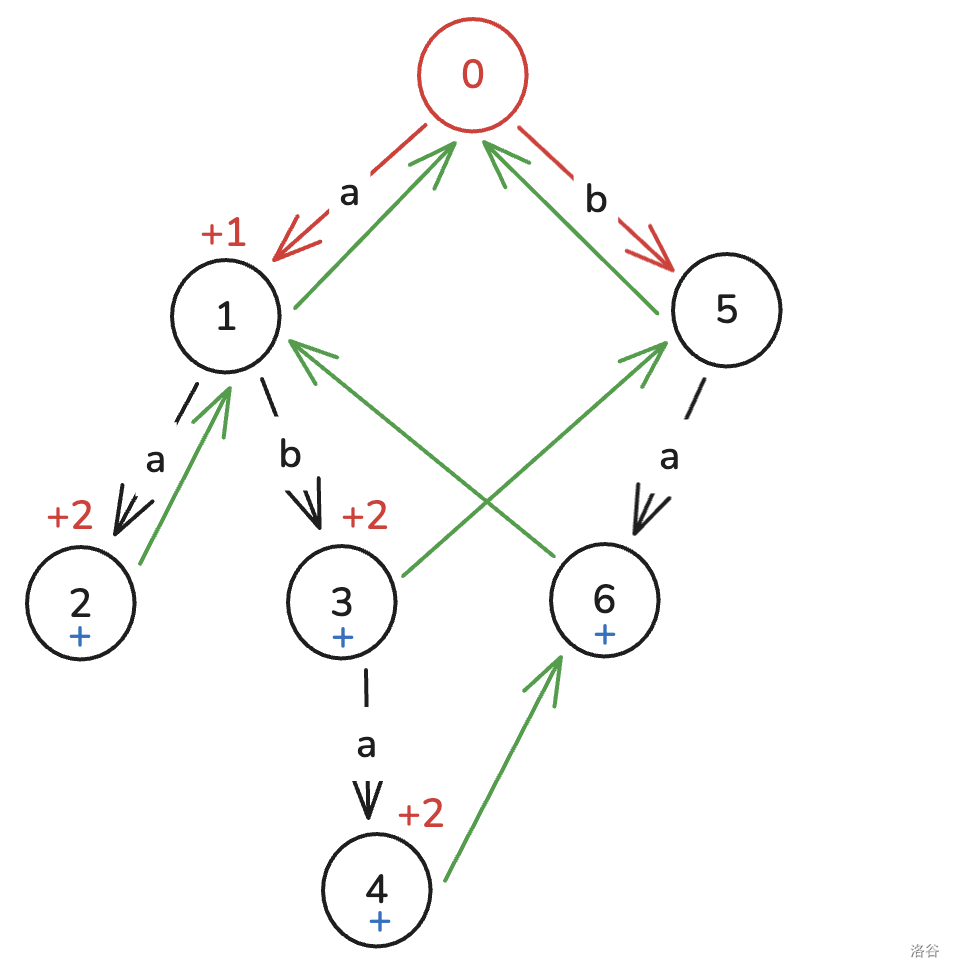
绿色的就是 fail 关系，构成了一棵树。

这个 AC 自动机怎么还有两棵树啊？分不清怎么办？其实说白了，字典树上的祖先是前缀，fail 树上的祖先是后缀。

那直接 dfs fail 树就好了，不过要记得在更新 fail 的时候顺便连边。

int dfs(int u)
{
    int res = tag[u];
    for (int v : g[u])
        res += dfs(v);
    for (int i : id[u])
        ans[i] = res;
    return res;
}

至此，原问题已经完美解决！让我们把所有元素结合在一起！

P5357 自动机代码 
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e5 + 5, S = 2e6 + 5;
int n, ans[N];
char s[S], t[N];

struct AC_auto
{
    int root = 1, tot = root, trie[N][30], fail[N], tag[N];
    vector<int> id[N], g[N];
    void insert(int cnt)
    {
        int pos = strlen(t + 1), u = root;
        for (int i = 1; i <= pos; i++)
        {
            int d = t[i] - 'a';
            if (!trie[u][d])
                trie[u][d] = ++tot;
            u = trie[u][d];
        }
        id[u].push_back(cnt);
    }
    void init_fail()
    {
        queue<int> q;
        q.push(root);
        fail[root] = root;
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            for (int i = 0; i < 26; i++)
            {
                if (!trie[u][i])
                    trie[u][i] = u == root ? 1 : trie[fail[u]][i];
                else
                {
                    fail[trie[u][i]] = u == root ? root : trie[fail[u]][i];
                    g[fail[trie[u][i]]].push_back(trie[u][i]);
                    q.push(trie[u][i]);
                }
            }
        }
    }
    void Pair()
    {
        int pos = strlen(s + 1);
        int u = root;
        for (int i = 1; i <= pos; i++)
        {
            u = trie[u][s[i] - 'a'];
            tag[u]++;
        }
    }
    int dfs(int u)
    {
        int res = tag[u];
        for (int v : g[u])
            res += dfs(v);
        for (int i : id[u])
            ans[i] = res;
        return res;
    }
    void debug(int u)
    {
        for (int i = 0; i < 26; i++)
            if (trie[u][i])
            {
                cout << u << ' ' << char('a' + i) << ' ' << trie[u][i] << endl;
                debug(trie[u][i]);
            }
    }
} ac;

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        scanf("%s", t + 1), ac.insert(i);
    ac.init_fail();
    scanf("%s", s + 1);
    ac.Pair();
    ac.dfs(ac.root);
    for (int i = 1; i <= n; i++)
        printf("%d\n", ans[i]);
    return 0;
}
例题：[NOI2011] 阿狸的打字机

https://www.luogu.com.cn/problem/P2414

还是考虑模式串对原串的贡献。发现是对原串进行一个到根的路径加（因为是每个前缀），再对模式串的 \(fail\) 子树进行子树 sum。

所以考虑离线下来，再进行一次遍历统计答案。把询问挂到原串对应点上，dfs 到这个点的时候，对询问进行模式串子树查询即可（要用 dfn 把子树转成区间）。

点击查看代码 
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 5;
int n, m;
char s[N];
vector<int> g[N];
int id[N], dfncnt, dfn[N], dfd[N];
vector<pair<int, int> > q[N];
int ans[N];

struct BIT
{
    int t[N];
    void add(int it, int x)
    {
        if (it <= 0)
            return;
        while (it <= 1e5)
        {
            t[it] += x;
            it += it & -it;
        }
    }
    int sum(int it)
    {
        int res = 0;
        while (it > 0)
        {
            res += t[it];
            it -= it & -it;
        }
        return res;
    }
} bit;

struct Ac_auto
{
    int root = 1, tot = 1, trie[N][30], fa[N], fail[N];
    void getFail()
    {
        queue<int> q;
        q.push(root);
        while (!q.empty())
        {
            int u = q.front(); q.pop();
            for (int c = 0; c < 26; c++)
            {
                if (!trie[u][c])
                    trie[u][c] = u == root ? root : trie[fail[u]][c];
                else
                {
                    fail[trie[u][c]] = u == root ? root : trie[fail[u]][c];
                    g[fail[trie[u][c]]].push_back(trie[u][c]);
                    q.push(trie[u][c]);
                }
            }
        }
    }
    void dfs(int u)
    {
        dfn[u] = ++dfncnt;
        for (int v : g[u])
            dfs(v);
        dfd[u] = dfncnt;
    }
    void solve(int u)
    {
        bit.add(dfn[u], 1);
        for (auto i : q[u])
            ans[i.second] = bit.sum(dfd[i.first]) - bit.sum(dfn[i.first] - 1);
        for (int c = 0; c < 26; c++)
            if (fa[trie[u][c]] == u)
                solve(trie[u][c]);
        bit.add(dfn[u], -1);
    }
    void debug(int u)
    {
        for (int i = 0; i < 26; i++)
            if (fa[trie[u][i]] == u)
            {
                cout << u << ' ' << char('a' + i) << ' ' << trie[u][i] << endl;
                debug(trie[u][i]);
            }
    }
} ac;

int main()
{
    scanf("%s", s + 1);
    int len = strlen(s + 1);
    int u = ac.root, v;
    for (int i = 1; i <= len; i++)
    {
        if (s[i] == 'B')
        {
            u = ac.fa[u];
        }
        else if (s[i] == 'P')
            id[++n] = u;
        else
        {
            int c = s[i] - 'a';
            if (!ac.trie[u][c])
            {
                ac.trie[u][c] = ++ac.tot;
                ac.fa[ac.tot] = u;
            }
            u = ac.trie[u][c];
        }
    }
    ac.getFail();
    ac.dfs(ac.root);
    cin >> m;
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d", &u, &v);
        q[id[v]].push_back({id[u], i});
    }
    ac.solve(ac.root);
    for (int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);
    return 0;
}

Manacher

可以线性处理出一个字符串的以 \(i\) 为中心的最长回文串长度。

模板题：P3805 【模板】manacher

这个东西其实非常简单啊，画个图就能理解了。

呃首先需要一个 trick，就是相邻的字符间插一个特殊字符，比如 |。然后开头（或结尾）也得插一个，否则开头结尾都是 0，可能会被判成回文串。

然后是 Manacher。

首先维护一个 \(r\) 表示目前遍历的 \(i\) 为中心的回文串中，回文串的右端点的最大值。以及一个 \(mid\) 表示这个 \(r\) 所对的回文串的中心。

假设我们已经处理了前 \(i-1\) 个 \(f\)，然后考虑当前的 \(i\)。设 \(j=2mid-i\)，即 \(i\) 关于 \(mid\) 的对称点。

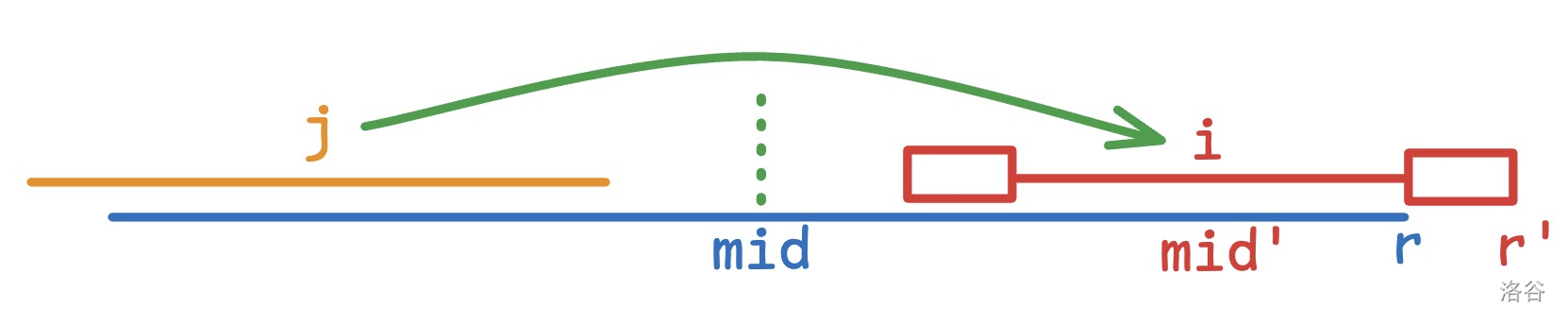
横线表示回文串，方框表示里面的内容相同。

  1. 如图。如果有 \(i + f_j - 1\ge r\)，那说明这个 \(i\) 很有潜力！从 \(f_i=\max(r-i+1,0)\) 开始（因为蕴含了 \(i>r\) 的情况），直接暴力判断、扩展 \(f_i\) 即可。因为 \(r\) 也会随之变大，所以这个扩展是均摊线性的。

  2. 否则，说明 \(i + f_j - 1\ge r\)，那直接让 \(f_i=i + f_j - 1\)，就不管它了。（没画，就是上图没有扩展）

点击查看代码 
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2.2e7 + 5;
int n, f[N], ans;
char s[N];

int main()
{
    s[n] = '~';
    s[++n] = '|';
    char c = getchar();
    while ('a' <= c && c <= 'z')
    {
        s[++n] = c;
        s[++n] = '|';
        c = getchar();
    }
    f[1] = 1;
    for (int i = 2, mid = 1, r = 1; i <= n; i++)
    {
        if (i + f[2 * mid - i] - 1 >= r)
        {
            f[i] = max(r - i + 1, 0);
            while (s[i + f[i]] == s[i - f[i]])
                f[i]++;
            mid = i, r = i + f[i] - 1;
        }
        else
            f[i] = f[2 * mid - i];
        ans = max(ans, f[i] - 1);
    }
    cout << ans << endl;
    return 0;
}

exKMP（Z函数）

P5410【模板】扩展 KMP/exKMP（Z 函数）

以线性时间，求一个字符串 \(s\) 的每个后缀与另一个字符串 \(t\) 的最长公共前缀（LCP）。

虽说这个叫做 exKMP，但它的思想是类似于 Manacher 的。

首先我们把 \(s\) 拼在 \(t\) 后面，那问题就转为了，对 \(t\) 的每一个（虽然用不着每一个）后缀求它与 \(t\) 的 LCP。

我们令 \(z_i\) 表示，从 \(i\) 开始的后缀的 LCP 长度。

还是假设处理了前面的 \(i-1\) 个，考虑当前。

仿照 Manacher，记录一个右端点最大的 LCP 的后缀信息，这个后缀以 \(k\) 开始，最大右端点为 \(r\)。

设 \(j=i-k+1\)，即 \(i\) 在蓝色横线中的对应位置。

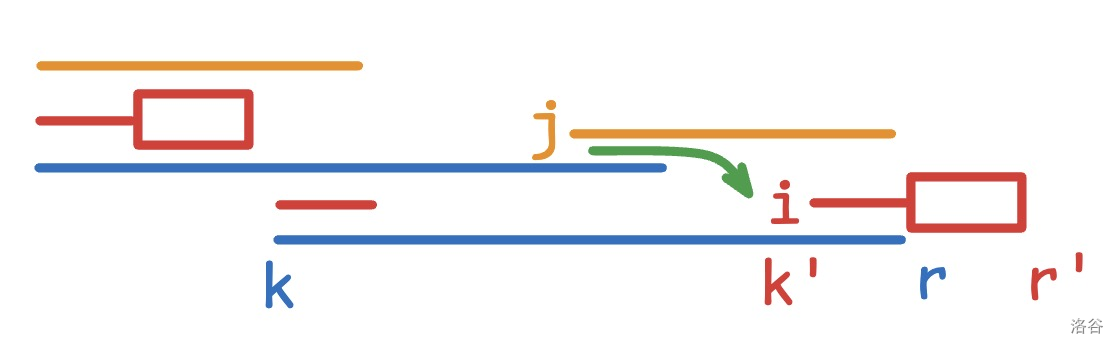
这回相同颜色的横线代表公共前缀。

  1. 如果 \(i+z_j+1\ge r\)，那还是让 \(z_i\) 到已知最大右端点，即让 \(z_i = \max(r-i+1,0)\)，然后再暴力扩展。

  2. 否则这个 \(i\) 就扩不了了，这辈子就只能这样了。

点击查看代码 
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 2e7 + 5;
int n, m, pos, z[N << 1];
char a[N], b[N], s[N << 1];

void exKMP()
{
    s[pos + 1] = '~';
    for (int i = 2, k = 1, r = 1; i <= pos; i++)
    {
        if (i == m + 1) // s[i] is '|'
            continue;
        if (i + z[i - k + 1] - 1 >= r)
        {
            z[i] = max(r - i + 1, 0);
            while (s[1 + z[i]] == s[i + z[i]])
                z[i]++;
            k = i, r = i + z[i] - 1;
        }
        else
            z[i] = z[i - k + 1];
    }
    z[1] = m;
}

int main()
{
    scanf("%s%s", a + 1, b + 1);
    n = strlen(a + 1), m = strlen(b + 1);
    for (int i = 1; i <= m; i++)
        s[++pos] = b[i];
    s[++pos] = '|';
    for (int i = 1; i <= n; i++)
        s[++pos] = a[i];
    exKMP();
    ll ans1 = 0, ans2 = 0;
    for (int i = 1; i <= m; i++)
        ans1 ^= 1ll * i * (z[i] + 1);
    for (int i = 1; i <= n; i++)
        ans2 ^= 1ll * i * (z[m + 1 + i] + 1);
    cout << ans1 << endl << ans2 << endl;
    return 0;
}

聪明的你一定发现了，这个代码和 Manacher 几乎一样！这不奇怪，因为它跟 Manacher 的思想是几乎一致的，只不过一个回文串、一个 LCP。它们都是用一个对应的 \(j\) 来更新自己的。当然 KMP 也差不多。

所以说这些字符串算法无非是从先前的信息中找到有用的信息，而不是再算一遍。

扯远了，继续讲。

回文自动机（PAM）

P5496【模板】回文自动机（PAM）

用来处理以 \(i\) 结尾的回文串信息。

这个也还挺好理解的，\(u\xrightarrow{c} v\) 表示 \(S_u \rightarrow c+S_u+c\)。

懒得详细讲了，因为看代码就能看懂。

  • root(0/-1) 表示回文串长度为偶/奇数时空串对应的节点
  • len 表示以 \(i\) 结尾的最长回文串（虽然这题不用）
  • ans 表示个数
  • trie, fail 类似 ACAM，表示树上的儿子、最长后缀对应的点
点击查看代码 
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e5 + 5;
int n, ans[N];
char s[N];

struct PAM
{
#define root(x) -x
    int tot = 1, trie[N][30], len[N], fail[N];
    int getFail(int u, int i)
    {
        while (s[i - len[u] - 1] != s[i])
            u = fail[u];
        return u;
    }
    void init()
    {
        len[root(0)] = 0, len[root(-1)] = -1;
        fail[root(0)] = fail[root(-1)] = root(-1);
        int cur, lst = root(-1);
        for (int i = 1; i <= n; i++)
        {
            if (i > 1)
                s[i] = (s[i] - 97 + ans[lst]) % 26 + 97;
            cur = getFail(lst, i);
            if (!trie[cur][s[i] - 'a'])
            {
                fail[++tot] = trie[getFail(fail[cur], i)][s[i] - 'a'];
                trie[cur][s[i] - 'a'] = tot;
                len[tot] = len[cur] + 2;
                ans[tot] = ans[fail[tot]] + 1;
            }
            lst = trie[cur][s[i] - 'a'];
            printf("%d%c", ans[lst], " \n"[i == n]);
        }
    }
} pam;

int main()
{
    scanf("%s", s + 1);
    n = strlen(s + 1);
    pam.init();
    return 0;
}

后缀数组（SA）

后缀自动机（SAM）

posted @ 2025-01-09 21:05  Aquizahv  阅读(27)  评论(0)    收藏  举报