决策单调性
前置知识:dp,分治,单调队列
对于一些 dp 转移,决策点 \(p_i\) 随着\(i\) 的增大而非严格递增。我们称这种转移有决策单调性。
判定
一般采用四边形不等式判定。
假设我们要解决如下一类问题:
\[f_{i} = \min_{1\le j\le i} w(j,i) \]若对于 \(a<b<c<d\),有
\[w(a,c)+w(b,d)\le w(a,d)+w(b,c) \]那么称函数 \(w\) 满足「四边形不等式」。此时 \(f_i\) 具有决策单调性。
证明不再赘述,想了解可以前往 OI Wiki - 四边形不等式优化。
另外 \(w(a,c)+w(a+1,c+1)\le w(a,c+1)+w(a+1,c)\) 也可以得到,可以看情况使用。
以及一般 dp 方程都是形如 \(f_i = \min_{1\le j\le i} w(j,i) = \min_{1\le j\le i} f_{j-1} + w'(j,i)\) 的东西,所以下文规定 \(f_i=\min_{1\le j\le i} f_{j-1} + w(j,i)\)。(四边形不等式两边都去掉 \(f_a + f_b\))
举一些 \(w(j,i)\) 的例子:
-
序列上一个区间内不同数字的个数,求 \(\max\)
-
\(|f(i)-f(j)+C|^P\)(\(f\) 为增函数,\(C\) 为常数,\(P\ge 1\)),求 \(\min\)
-
\((f(i)-f(j)+C)^P\)(\(f\) 为增函数,\(C\) 为常数,\((f(i)-f(j)+C\ge0)\),\(P\le 1\)),求 \(\max\)
现在尝试证明它们是否满足 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)。
对于 1,考虑设四个端点分成的三个段的值分别为 \(X,Y,Z\)。
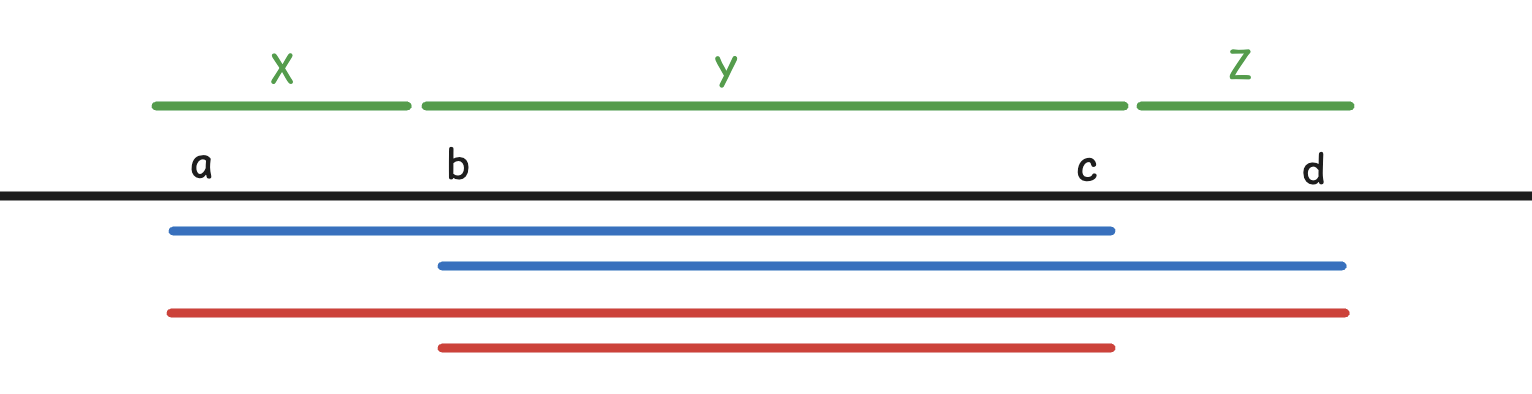
因此 \(w(a,c)+w(b,d)\ge w(a,d)+w(b,c)\),符号相反!
但注意到定理描述里写的是 \(\min\),而问题中是 \(\max\),所以有决策单调性。
对于 2 和 3,增函数常作为前缀和出现。
注意到 \(f\) 之间会作差,所以还是考虑分段设。
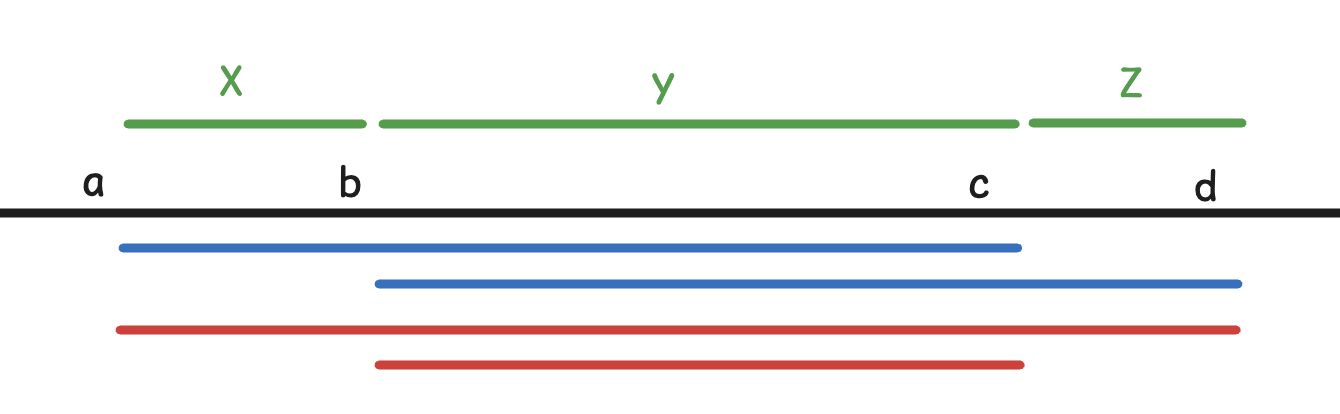
对于 2:
(其实上面公式打最后一行时需要一直按着 shift)
随便画一个 \(y=|x|^P(P>1)\),发现一定是凹的。
然后把几个点画出来,发现有公共中点 \(C+Y+\frac{X+Z}{2}\)。
中点能干什么?连接对应点,\(y\) 坐标之和即为中点 \(y\) 坐标值的两倍。

显然,在一个凹函数上,这样的两对点,一定是长线段中点在短线段之上。
因此有 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\),当且仅当 P=1 时取等。
对于 3,也是类似的,可以画几个 \(P<1\) 的幂函数出来看看。
比如 \(y=x^{1/2}\),当 \(x\) 非负为凸函数。\(y=x^{1/3}\) 也是。而就算加上绝对值,也无法使成为全定义域的凸函数。所以就要 \(f(i)-f(j)+C\ge0\)。
同样的,这个是 \(w(a,c)+w(b,d)\ge w(a,d)+w(b,c)\),但是取的 \(\max\) 就反过来变为 \(\le\)。
总之上面 3 个就都是有决策单调性的。
实现
比较主流的实现方式有分治、单调队列、二分栈。
分治
不是所有决策单调性 dp 都能分治优化,分治优化要求转移的东西能快速、独立算出。
什么叫独立呢?就是不依赖于举个例子,如果 \(f_i=min_{j<i}\{f_j+w(i,j)\}\),那说明 \(f_i\) 依赖于之前 \(f_j\) 的值,无法独立得出。
但是如果是 \(f_{k,i}=min_{j<i}\{f_{k-1,j}+w(i,j)\}\),那么 \(f_{k-1}\) 的值已经知道,没有依赖于
例题
给你一个长度为 \(n\) 的序列 \(A_1,A_2,...,A_n\),一开始把它看作一个块。初始你的分数为 \(0\),现在你需要进行下列操作恰好 \(m\) 次:
- 选一个块,并从一处断开,使得断开的两个块不为空。此时这两个块里的数的和的乘积将加到你的分数里。
求最终分数的最大值,并输出断开的位置。
\(2 \le n \le 10^5,1\le m\le\min\{n-1,200\},0\le A_i\le 10^4\)。
(注:由于本题解的状态转移方程需要用到 \(k\),所以原题中的 \(k\) 对应本题解中的 \(m\)。)
这个分数的计算有点绕,我们考虑一下两个位置 \((i,j)\) 的贡献:不难发现,当且仅当这两个位置最终不在一个块内时,对答案产生 \(A_i \times A_j\) 的贡献。
正难则反,用总和减去不产生贡献的,即每个块内的和的平方和,那么答案就是:
于是我们就成功把原问题转化为了这么一个问题:
有一个长度为 \(n\) 的序列,现在要将序列划分为 \(m+1\) 段,最小化各段和的平方之和。
设 \(f_{k,i}\) 表示第 \(k\) 段的末尾是 \(i\),当前的总和的最小值。
则有
设 \(w(i,j)\) 为 $(\sum_{l=j+1}^i A_l)^2 $,即 \((sum_i-sum_j)^2\)。
显然 \(sum\) 是递增函数,因此根据之前的结论, \(w(i,j)\) 满足四边形不等式。所以 \(f_k\) 有决策单调性。
观察转移式,注意到 \(f_k\) 从 \(f_{k-1}\) 转移,也就是说 \(f_{k,i}\) 间没有依赖,所以这题也可以分治优化 dp。
递归参数 \((l,r,x,y)\) 表示 \([l,r]\) 的 dp 值待计算,并且决策点位于 \([x,y]\)。每次遍历 \([x,y]\),计算 \(mid=\lfloor\frac{l+r}{2}\rfloor\) 位置的 dp 值,然后递归 \((l,mid-1,x,op_{mid})\) 和 \((mid+1,r,op_{mid},y)\)。
时间复杂度 \(O(mn\log n)\)。
(还有一个 \(P<1\) 的:[POI 2011] Lightning Conductor,值得一提的是 dp 的时候要保留小数,不然不满足决策单调性)
ll cal(int l, int r)
{
return sq(sum[r] - sum[l - 1]);
}
void solve(int l, int r, int x, int y)
{
int mid = (l + r) >> 1;
for (int i = x; i <= y && i <= mid; i++)
{
ll w = dp[k - 1][i - 1] + cal(i, mid);
if (dp[k][mid] > w)
{
dp[k][mid] = w;
op[k][mid] = i;
}
}
if (l < mid)
solve(l, mid - 1, x, op[k][mid]);
if (mid < r)
solve(mid + 1, r, op[k][mid], y);
}
单调队列
那么如果需要依赖之前的 dp 值怎么办呢?
我们维护一个双端队列,元素有三个属性 \((j,l,r)\) 表示目前 \(f_l \sim f_r\) 的值用 \(j\) 更新最优。
以下令 \(g_{j,i}\) 表示 \(f_j+w(i,j)\)。
第 \(i\) 轮时进行如下操作:
一、弹队首
-
取出队首 \((j,l,r)\)
-
若 \(r<i\),回到 1;否则 \(f_i=g_{j,i}\)。
二、弹队尾、入队尾
-
取出队尾 \((j,l,r)\)
-
若 \(g_{i,l}<g_{j,l}\),回到 1
-
二分查找 \((l,r]\) 中最小的 \(k\) 满足 \(g_{i,k}<g_{j,k}\),若不存在则 \(k=r+1\)
-
入队 \((j,l,k-1)\)、\((i,k,n)\)
简单来说就是动态维护每个 \(j\) 负责哪段 \(i\) 的决策。然后这个操作比较像单调队列,所以大家就叫它单调队列。
带一只 log。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号