【学习笔记】网络流
本文目前在不定期更新。
网络流定义
「网络」是指一张特殊的有向图,其中有一个「源点」\(s\) (不是记忆源点)和一个汇点 \(t\),然后每条边都有一个「容量」。网络中的「流」是指一种方案,每条边都有一个「流量」,使得边的「流量」不超过其「容量」,并且对于除 \(s\)、\(t\) 以外的任意一个点 \(u\),都有
在某些语境下,「流」代表一个值,是 \(t\) 的所有入边的「流量」之和。
最大流
给你一张网络,每条边有一个「容量」\(c\)。你需要求出从 \(S\) 到 \(T\) 的网络最大流。
思想
首先一开始对每条边建立一条容量为 \(0\) 的反向边。
然后每轮执行以下操作:
- 在残量网络(即还能流的网络)中找到一条 \(s\) 到 \(t\) 的增广路。
- 令 \(w=\) 增广路所有边剩余容量的最小值。则:
- \(ans\) += \(w\)
- 增广路上所有边的剩余容量 -= \(w\)
- 增广路上所有反向边的剩余容量 += \(w\)
举个典型的例子:

显然,最大流为 \(2\),就是上面一条和下面一条。但是我们的程序没有那么聪明,他有可能找出一条这样的路:
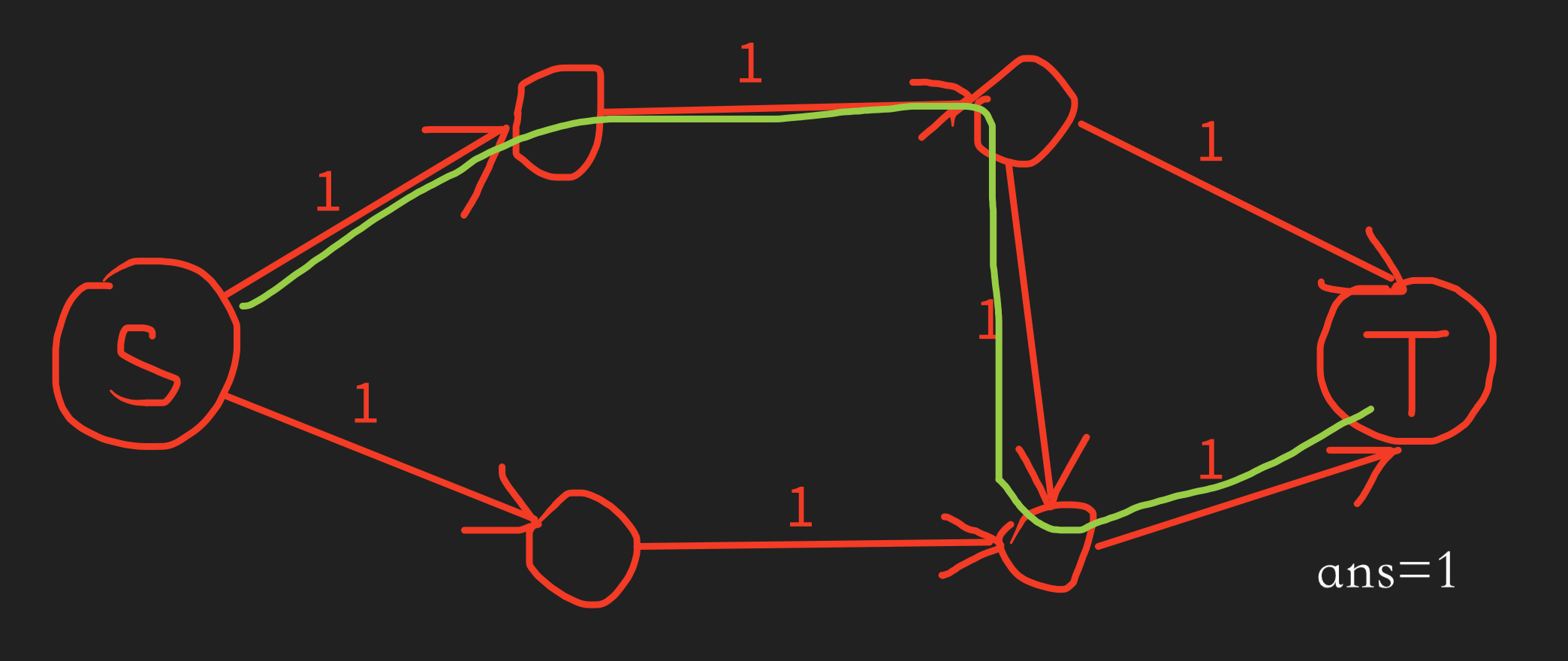
此时答案加一,然后进行反悔操作:(反向边容量为 0 的没有画出来)
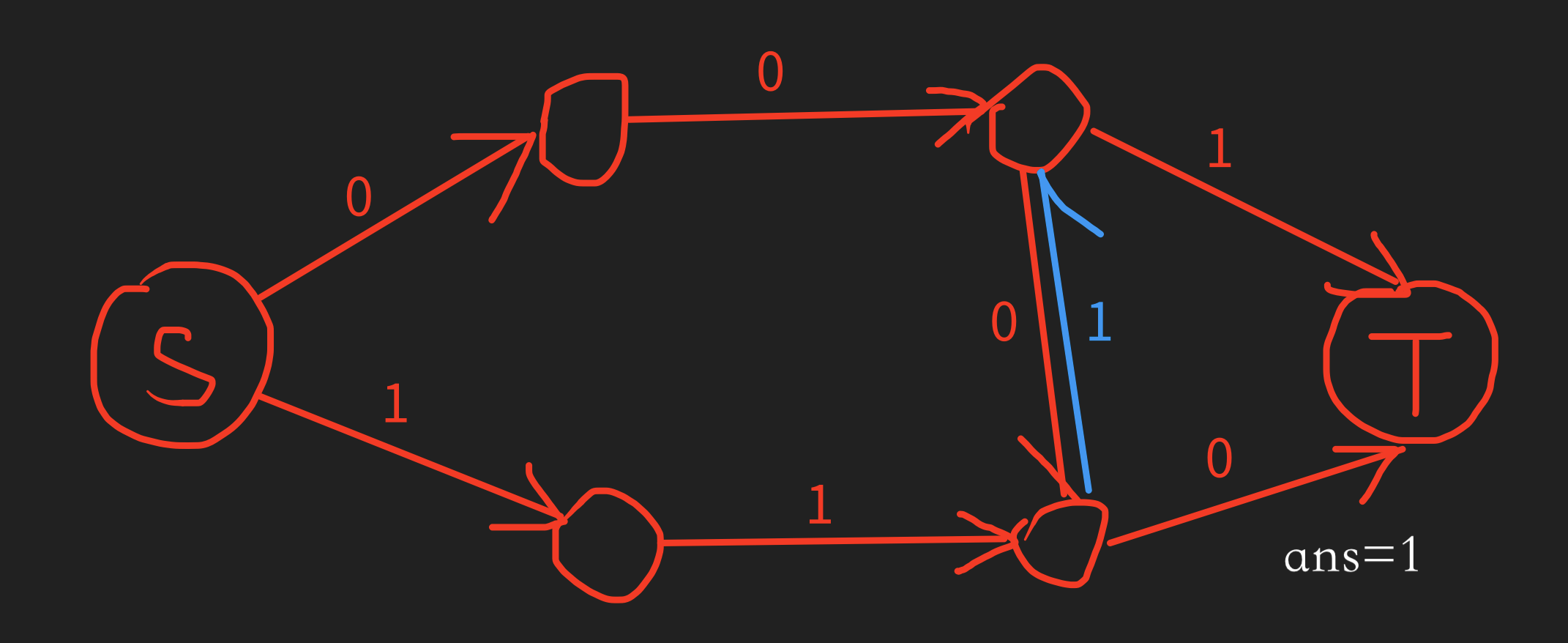
然后此时程序又找到了一条经过反向边的增广路,于是答案再加一:
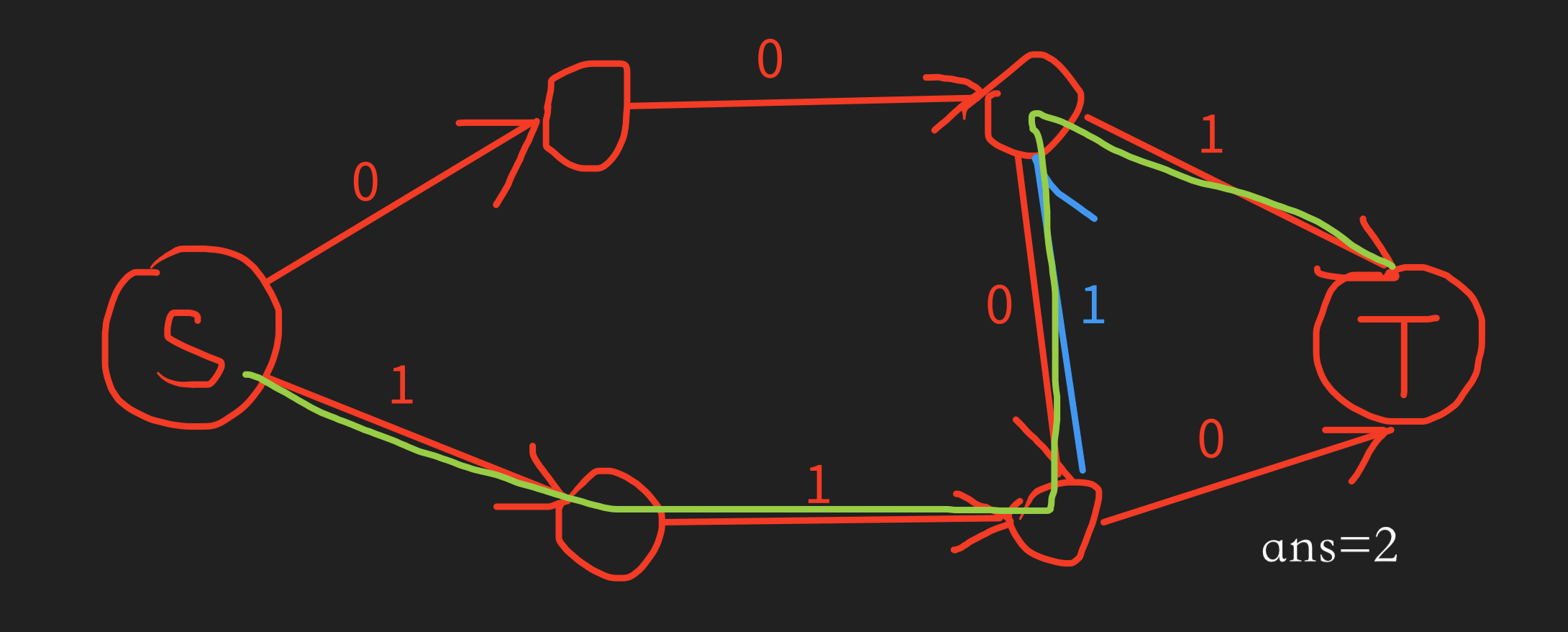
然后就得到了想要的结果,因为这个方案跟我们的方案是本质一样的。
至于原理可以参考匈牙利算法。刚刚的反悔就相当于,寻找一个点的匹配时,是否可以换掉别人的匹配。
比如这张图中,第二条路径本来想要直接从下面到 \(t\),但是那条边的流量已经满了。所以我们让原本在那里的水,沿着中间跨过来的边流回去。这个操作就等价于那个反悔操作。
那么不难看出,以上就是一种很正确的带有反悔行为的策略。
但是还有一个问题,没有增广路了就说明找到最大流了吗?答案是肯定的,参见 OI-wiki上的证明
FF算法
FF 算法就是把最大流的思想用最直接的方式实现,即 dfs 找增广路。
但是,dfs 有时会效率很低,如:

此时用 dfs 的话可能会出现以下的过程:
\(s \rightarrow 1 \rightarrow 2 \rightarrow t\),\(s \rightarrow 2 \rightarrow 1 \rightarrow t\),\(s \rightarrow 1 \rightarrow 2 \rightarrow t\),\(s \rightarrow 2 \rightarrow 1 \rightarrow t\),……
那要是边权从 \(100\) 变为 \(inf\) 不就爆炸了。
EK算法
在 FF 算法上做一个“简单”的优化:每次找一条边数最少的增广路,也就是把 dfs 换成 bfs。这就是 EK 算法。感觉效率高了一些!
分析一下时间复杂度。这里引入一个结论:增广总轮数的上界是 \(\mathcal{O}(nm)\)(证明不会qwq,想了解的可以去 OI-Wiki),然后每次的 bfs 是 \(\mathcal{O}(n+m)\) 的,所以是 \(\mathcal{O}(nm^2)\)。
然而这个 \(\mathcal{O}(nm^2)\) 常常卡不满,在随机数据和稀疏图下跑的很快。
点击查看代码
// Author: AquariusZhao
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
const int N = 205;
int n, m, pre[N];
ll g[N][N], flow[N];
ll bfs(int s, int t)
{
memset(pre, -1, sizeof(pre));
flow[s] = inf;
pre[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty())
{
int u = q.front();
q.pop();
if (u == t)
return flow[t];
for (int v = 1; v <= n; v++)
if (pre[v] == -1 && g[u][v] > 0)
{
pre[v] = u;
q.push(v);
flow[v] = min(flow[u], g[u][v]);
}
}
return -1;
}
ll maxflow(int s, int t)
{
ll res = 0;
while (true)
{
ll x = bfs(s, t);
if (x == -1)
break;
int v = t;
while (v != s)
{
int u = pre[v];
g[u][v] -= x;
g[v][u] += x;
v = u;
}
res += x;
}
return res;
}
int main()
{
int s, t;
cin >> n >> m >> s >> t;
int u, v, w;
for (int i = 1; i <= m; i++)
scanf("%d%d%d", &u, &v, &w), g[u][v] += w;
printf("%lld\n", maxflow(s, t));
return 0;
}
以上代码建议理解,但没必要背下来,因为下面要讲的 Dinic 算法比它快而且码量差不多。
Dinic算法
EK 算法每次找增广路都要跑一遍 bfs,是不是有点浪费了呀……每次只能找一条路径,而计算完流量后又要从新开始。为什么不能在之前的结果上继续找呢?
Dinic 算法可以看作 EK 算法的优化†,它会不断执行以下步骤直到 bfs 时发现走不到 \(t\):
- 用 bfs 给每个点定一个 \(dep\),表示从该点到 \(s\) 的最短距离;
- 用 dfs 找增广路,但是深度为 \(dep\) 的点只能走到 \(dep+1\) 的点。
†虽然 Dinic 算法可以看作 EK 算法的优化,但后者其实要出现的晚一些。
另外,Dinic 算法有两个优化,详见代码。(好像还有一些厉害的优化,但不太实用,想了解可以去看看 P4722 【模板】最大流 加强版 / 预流推进 的题解区关于 Dinic 的其他优化。)
点击查看代码
// Author: AquariusZhao
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N = 205, M = 5005;
int n, m, s, t;
int pos = 1, head[N], now[N];
struct node
{
int u, v, w, nxt;
} e[M << 1];
ll ans;
void addEdge(int u, int v, int w)
{
e[++pos] = {u, v, w, head[u]};
head[u] = pos;
}
int dep[N];
bool bfs()
{
memset(dep, -1, sizeof(dep));
dep[s] = 0;
queue<int> q;
q.push(s);
now[s] = head[s];
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == -1)
{
dep[v] = dep[u] + 1;
now[v] = head[v];
q.push(v);
if (v == t)
return true;
}
}
}
return false;
}
ll dfs(int u, ll sum)
{
if (u == t)
return sum;
ll res = 0;
for (int &i = now[u]; i; i = e[i].nxt) // 优化一:当前弧优化,走到第i条边时sum还>0,说明前面的边到汇点没有增广路了,下次不必再走
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == dep[u] + 1)
{
ll x = dfs(v, min(sum, (ll)(e[i].w)));
if (x == 0) // 优化二:如果从v找不到增广路了,可以将dep设为-1,以后就不会再搜了
dep[v] = -1;
e[i].w -= x;
e[i ^ 1].w += x;
sum -= x;
res += x;
}
if (sum <= 0)
break;
}
return res;
}
int main()
{
cin >> n >> m >> s >> t;
int u, v, w;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &u, &v, &w);
addEdge(u, v, w), addEdge(v, u, 0);
}
while (bfs())
ans += dfs(s, inf);
cout << ans << endl;
return 0;
}
Dinic 时间复杂度
参考了 myee 的博客、OI-wiki 上的 Dinic 时间复杂度分析以及特殊情形下的时间复杂度分析。
比较通用的 Dinic 算法的时间复杂度是 \(\mathcal{O}(n^2m)\),增广 \(O(n)\) 轮,每轮复杂度 \(O(nm)\)
还有一种是 \(O(\sqrt{\sum \min\{in_u,out_u\}}\sum w_i)\),其中 \(in_u\) 表示 \(u\) 入边容量和,\(out_u\) 出边容量和。
但是有一些特殊情况可以用其他计算方式。
各边容量为 \(1\) 的网络:\(O(m\min\{m^{\frac{1}{2}},n^{\frac{2}{3}}\})\)。
单位网络:\(O(m\sqrt{n})\)。单位网络是一类特殊的各边容量均为 1 的网络,满足除源汇外各点入度不超过 1 或出度不超过 1。
在稀疏图、稠密图上的分析:
| 稀疏图(\(m\sim n\)) | 稠密图(\(m\sim n^2\)) | |
|---|---|---|
| 一般网络 | \(O(n^3)\) | \(O(n^4)\) |
| 各边容量为 1 的网络 | \(O(n\sqrt{n})\) | \(O(n^{\frac{8}{3}})\) |
| 单位网络 | \(O(n\sqrt{n})\) | \(O(n^{\frac{5}{2}})\) |
但是永远记住一点:一般卡不满()
最小割
对于一个网络,一个「割」是在网络中删掉一些边之后,\(s\) 和 \(t\) 不连通的方案。而此时点会被划分成两个集合 \(S\) 和 \(T\),其中 \(s \in S\),\(t \in T\)。割也常常代指一个割的费用。
最小割问题:求所有割中总费用最小的。
其实,在一张网络中,\(s\) 到 \(t\) 的最大流 \(=\) \(s\) 到 \(t\) 的最小割。
我觉得这个结论比较显然。考虑一个最大流,则此时找不到从 \(s\) 到 \(t\) 到增广路了,所以那些 \(s\) 能到达(只走有残余容量的边)的点集就是 \(S\),而剩余的就是\(T\)。此时对于所有边 \(\{(u,v)|u \in S,v\in T\}\),残余容量为 \(0\),选这些边为此时的最小的割,并且等于总流量。故最小割都等于最大流。也可以得出:流一定不大于最小割,割一定不小于最大流。
严谨的证明还是前往 OI-wiki 吧。qwq
最大权闭合图
指的是这样一类问题:
有 \(n\) 个物品,每个物品有价值 \(w_i\),可正可负。
有 \(m\) 个限制,形如 \((a_i,b_i)\),表示如果选了第 \(a_i\) 个物品就必须选 \(b_i\)。
最大化选出物品的价值和。
套路做法是,
\(s\xrightarrow{w_i} i(w_i\ge0)\)
\(a_i\xrightarrow{\infty}b_i\)
\(i\xrightarrow{-w_i}t(w_i<0)\)
答案就是
原因是,对于某个限制,先考虑 \(w_{a_i}\ge 0,w_{b_i}<0\),则只能割 \(s\) 侧或者 \(t\) 侧(而不是限制)。如果割 \(s\) 侧,相当于没有选这个正权物品(\(a_i\)),丢失 \(w_i\) 的正贡献;如果割 \(t\) 侧,那么这个这对 \((a_i,b_i)\) 就选了,而造成 \(-w_i\) 的负贡献。
关键的思想是取了“不取正而丢失的价值”和“取负而丢失的价值”的较小值。
P4174 [NOI2006] 最大获利
板子题。如果得到一个用户的收益,那必须付出建两个中转站的代价。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 1e5 + 5, M = 2e5 + 5;
int n, m, p[N], s, t;
int head[N], pos = 1;
struct Edge
{
int u, v, w, nxt;
} e[M << 1];
void addEdge(int u, int v, int w)
{
e[++pos] = {u, v, w, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0);
}
int dep[N], now[N];
bool bfs()
{
queue<int> q;
q.push(s);
memset(dep, -1, sizeof(dep));
dep[s] = 0;
now[s] = head[s];
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == -1)
{
dep[v] = dep[u] + 1;
now[v] = head[v];
if (v == t)
return true;
q.push(v);
}
}
}
return false;
}
int dfs(int u, int sum)
{
if (u == t)
return sum;
int res = 0;
for (int &i = now[u]; i; i = e[i].nxt)
{
int v = e[i].v, w = e[i].w;
if (w > 0 && dep[v] == dep[u] + 1)
{
int x = dfs(v, min(sum, w));
if (x == 0)
dep[v] = -1;
e[i].w -= x;
e[i ^ 1].w += x;
sum -= x;
res += x;
}
if (sum <= 0)
break;
}
return res;
}
int Dinic()
{
int res = 0;
while (bfs())
res += dfs(s, inf);
return res;
}
int main()
{
cin >> n >> m;
s = 0, t = n + m + 1;
int sum = 0;
for (int i = 1; i <= n; i++)
{
scanf("%d", p + i);
addEdge(m + i, t, p[i]);
}
int u, v, w;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &u, &v, &w);
sum += w;
addEdge(s, i, w);
addEdge(i, m + u, inf);
addEdge(i, m + v, inf);
}
cout << sum - Dinic() << endl;
return 0;
}
P2762 太空飞行计划问题
和刚刚那题几乎一模一样,但是要输出方案。
我们规定,如果过不了限制边就是 \(s\) 的,否则是 \(t\)。可以通过查询 dep 是否为 -1 来判断某一个点是否可达,可达就说明选了。
输出方案
for (int i = 1; i <= m; i++)
if (dep[i] != -1)
printf("%d ", i);
puts("");
for (int i = 1; i <= n; i++)
if (dep[i + m] != -1)
printf("%d ", i);
puts("");
$\color{red}常见误区$
注意,不能通过判断边的容量是否用光来确定连通性。因为有可能 \(t\) 侧的边容量空了,但是在 \(s\) 侧就已经断了。
比如考虑一条 \(s\xrightarrow{1} a\rightarrow b\xrightarrow{1}t\) 的路径,跑完最大流之后有 \(s\xrightarrow{0} a\) 和 \(b\xrightarrow{0} t\),但下面的错误代码会认为两个地方都断了。
总之错误原因就是判断依据不充分。
错误代码:
for (int i = head[s]; i; i = e[i].nxt)
if (e[i].w)
printf("%d ", e[i].v);
puts("");
for (int i = head[t]; i; i = e[i].nxt)
if (e[i ^ 1].w == 0)
printf("%d ", e[i].v - m);
puts("");
CF103E Buying Sets
如果得到一个集合的价值,集合里的数都必须选。但是由于要求最小方案所以集合权值取反一下。
但是题目要求选集合数要等于选的数的个数,不过满足任意多个集合的并集大小不小于集合数。所以采用套路,把所有数的权值 \(-inf\),集合权值 \(+inf\),这样如果数比集合多就会很小,强制个数相等。于是完美转化为了最大权闭合图。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 605, M = 1e5, inf = 1e9;
int n;
int head[N], pos = 1;
struct Edge
{
int u, v, w, nxt;
} e[M << 1];
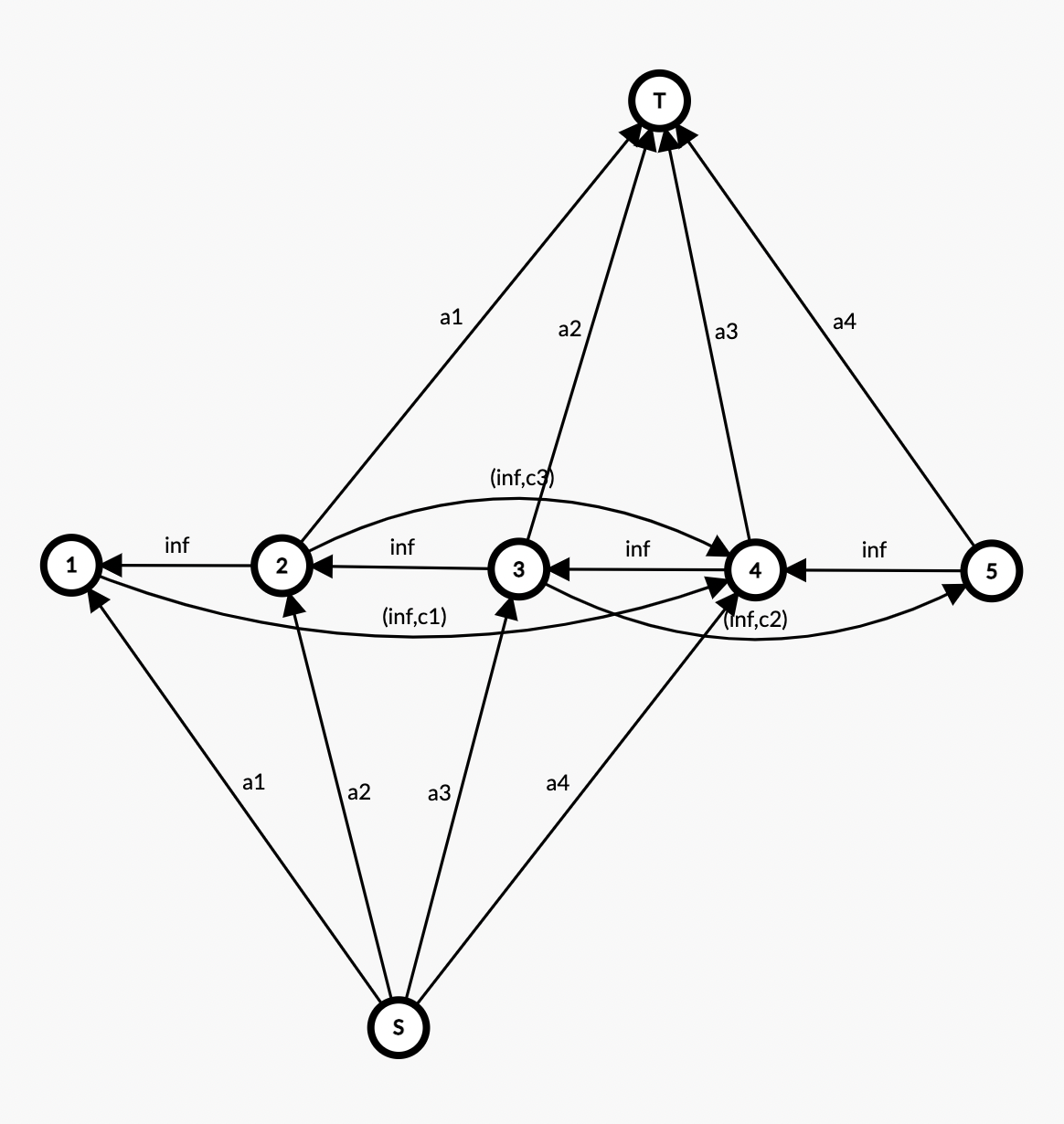
void addEdge(int u, int v, int w)
{
e[++pos] = {u, v, w, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0);
}
int s, t, dep[N], now[N];
bool bfs()
{
queue<int> q;
q.push(s);
memset(dep, -1, sizeof(dep));
dep[s] = 0;
now[s] = head[s];
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == -1)
{
dep[v] = dep[u] + 1;
now[v] = head[v];
if (v == t)
return true;
q.push(v);
}
}
}
return false;
}
ll dfs(int u, ll sum)
{
if (u == t)
return sum;
ll res = 0;
for (int &i = now[u]; i; i = e[i].nxt)
{
int v = e[i].v;
ll w = e[i].w;
if (w > 0 && dep[v] == dep[u] + 1)
{
ll x = dfs(v, min(sum, w));
if (x == 0)
dep[v] = -1;
e[i].w -= x;
e[i ^ 1].w += x;
sum -= x;
res += x;
}
if (sum <= 0)
break;
}
return res;
}
ll Dinic()
{
ll res = 0;
while (bfs())
res += dfs(s, inf);
return res;
}
int main()
{
cin >> n;
s = 0, t = n + n + 1;
int m, v;
for (int i = 1; i <= n; i++)
{
scanf("%d", &m);
while (m--)
scanf("%d", &v), addEdge(i, v + n, inf);
}
ll sum = 0;
for (int i = 1; i <= n; i++)
{
scanf("%d", &v), addEdge(s, i, inf - v);
sum += inf - v;
addEdge(i + n, t, inf);
}
cout << -(sum - Dinic()) << endl;
return 0;
}
最大密度子图
给定一张无向图。选出一个点集,则这个点集的密度为 \(\frac{点集内边数}{点数}\)。
求出所有点集的最大密度。
考虑分数规划。二分一个 \(mid\)。
则条件转为 \(边数 - 点数\times mid\ge0\)。
边产生 1 的贡献,且需要选上端点;点产生 \(-mid\) 的贡献。跑最大权闭合图即可。
其他经典最小割模型
最小割树
问题:给一张带权无向图,询问任意两点间最小割。
解决方式是一个分治的思想:
在当前点集(初始就是原图点集)随便找两个点求一下最小割,同时维护一棵树,每次求完割就连接这两个点,边权为最小割。然后把割成的两个点集再递归下去。注意最小割要在原图上求。
然后就可以建成一棵树。则任意两点的最小割就是树上两点路径上的最小边权。
证明还在想,先咕着
时间复杂度 \(\mathcal{O}(n^2 + 卡不满的n^3m)\)。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 505, M = 1505;
int n, m;
int head[N], pos = 1;
struct Edge
{
int u, v, w, nxt;
} e[M << 2];
vector<pair<int, int> > g[N];
void addEdge(int u, int v, int w)
{
e[++pos] = {u, v, w, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0);
}
int s, t, dep[N], now[N];
void init()
{
for (int i = 2; i <= pos; i += 2)
{
e[i].w += e[i ^ 1].w;
e[i ^ 1].w = 0;
}
}
bool bfs()
{
queue<int> q;
memset(dep, -1, sizeof(dep));
q.push(s);
dep[s] = 0;
now[s] = head[s];
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dep[v] == -1)
{
dep[v] = dep[u] + 1;
now[v] = head[v];
if (v == t)
return true;
q.push(v);
}
}
}
return false;
}
int dfs(int u, int sum)
{
if (u == t)
return sum;
int res = 0;
for (int &i = now[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == dep[u] + 1)
{
int x = dfs(v, min(e[i].w, sum));
if (!x)
dep[v] = -1;
e[i].w -= x;
e[i ^ 1].w += x;
sum -= x;
res += x;
}
if (sum <= 0)
break;
}
return res;
}
int Dinic(int x, int y)
{
init();
s = x, t = y;
int res = 0;
while (bfs())
res += dfs(s, inf);
return res;
}
void Dfs(vector<int> o)
{
if (o.size() < 2)
return;
int w = Dinic(o[0], o[1]);
g[o[0]].push_back({o[1], w});
g[o[1]].push_back({o[0], w});
vector<int> v1, v2;
for (auto u : o)
{
if (dep[u] != -1)
v1.push_back(u);
else
v2.push_back(u);
}
Dfs(v1);
Dfs(v2);
}
bool vis[N];
int query(int s, int t)
{
queue<pair<int, int> > q;
q.push({s, inf});
memset(vis, 0, sizeof(vis));
vis[s] = true;
while (!q.empty())
{
auto cur = q.front();
q.pop();
if (cur.first == t)
return cur.second;
for (auto i : g[cur.first])
{
if (!vis[i.first])
{
q.push({i.first, min(cur.second, i.second)});
vis[i.first] = true;
}
}
}
return inf;
}
int main()
{
cin >> n >> m;
int u, v, w;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &u, &v, &w);
addEdge(u, v, w), addEdge(v, u, w);
}
vector<int> _v;
for (int i = 1; i <= n; i++)
_v.push_back(i);
Dfs(_v);
int Q;
cin >> Q;
while (Q--)
{
scanf("%d%d", &u, &v);
printf("%d\n", query(u, v));
}
return 0;
}
CF343E Pumping Stations
首先把最小割树建出来。
然后考虑分治,先把当前最小的边割了。这样就变成了两个连通块,然后就分成了两个子问题,一半走完再跨过这个边走另一半。如此,每条边都恰好产生一次贡献。
首先显然不会有答案比这个还优了。
其次,我一开始觉得边有可能会经过两次,毕竟有时走完另一半之后要回来再走一次这个边,走到之前那一半。
然而实际上,这种情况下,这条边不会产生贡献。因为你既然走完另一半,那就意味着整个连通块的点都走过了,却还要回来,说明他肯定会退出这个连通块,经过这个连通块的父亲边,贡献就肯定不属于它了(因为从小往大割的)。
那其实就已经证完了,只有其中一半走完再走向另一半才会有贡献。如果再回来就必然没有贡献。
所以,答案就是最小割树上的边权和(这也说明一个性质,无论最小割树是怎么建的,边权的集合一定一样),排列就是 dfs 序。
希望不会有人像我一样傻傻的以为建树过程就是割最小边。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 205, O = 205, M = 2005;
int n, m, ans;
vector<int> res;
int head[O], pos = 1;
struct Edge
{
int u, v, w, nxt;
} e[M << 1];
void addEdge(int u, int v, int w)
{
e[++pos] = {u, v, w, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0);
}
int s, t, dep[O], now[O];
bool bfs()
{
queue<int> q;
q.push(s);
memset(dep, -1, sizeof(dep));
dep[s] = 0;
now[s] = head[s];
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w > 0 && dep[v] == -1)
{
dep[v] = dep[u] + 1;
now[v] = head[v];
if (v == t)
return true;
q.push(v);
}
}
}
return false;
}
int dfs(int u, int sum)
{
if (u == t)
return sum;
int res = 0;
for (int &i = now[u]; i; i = e[i].nxt)
{
int v = e[i].v, w = e[i].w;
if (w > 0 && dep[v] == dep[u] + 1)
{
int x = dfs(v, min(sum, w));
if (x == 0)
dep[v] = -1;
e[i].w -= x;
e[i ^ 1].w += x;
sum -= x;
res += x;
}
if (sum <= 0)
break;
}
return res;
}
int Dinic()
{
int res = 0;
while (bfs())
res += dfs(s, inf);
return res;
}
void init()
{
for (int i = 2; i <= pos; i++)
{
e[i].w += e[i ^ 1].w;
e[i ^ 1].w = 0;
}
}
int Pos = 1, Head[N];
Edge E[N << 1];
void AddEdge(int u, int v, int w)
{
E[++Pos] = {u, v, w, Head[u]};
Head[u] = Pos;
}
void Dfs(vector<int> o) // build tree
{
if (o.size() < 2)
return;
s = o[0], t = o[1];
init();
int w = Dinic();
ans += w;
AddEdge(s, t, w), AddEdge(t, s, w);
vector<int> v1, v2;
for (auto u : o)
{
if (dep[u] != -1)
v1.push_back(u);
else
v2.push_back(u);
}
Dfs(v1);
Dfs(v2);
}
int mnw, mne;
void DFS(int u, int fa) // find min edge
{
for (int i = Head[u]; i; i = E[i].nxt)
if (E[i].w && E[i].v != fa)
{
if (E[i].w < mnw)
mnw = E[i].w, mne = i;
DFS(E[i].v, u);
}
}
void DFs(int u) // dfs tree
{
mnw = inf;
DFS(u, 0);
if (mnw == inf)
{
res.push_back(u);
return;
}
E[mne].w = E[mne ^ 1].w = 0;
int tmp = mne;
DFs(E[tmp].u);
DFs(E[tmp].v);
}
int main()
{
cin >> n >> m;
int u, v, w;
for (int i = 1; i <= m; i++)
scanf("%d%d%d", &u, &v, &w), addEdge(u, v, w), addEdge(v, u, w);
vector<int> o;
for (int i = 1; i <= n; i++)
o.push_back(i);
Dfs(o);
DFs(1);
cout << ans << endl;
for (auto u : res)
printf("%d ", u);
return 0;
}
费用流
最小费用最大流,简称费用流。
这种问题的网络边还有一个权值 \(cost\) 表示这条边的每一单位流量都要 \(cost\) 的费用(以后说边权 \((w,c)\) 就表示容量为 \(w\),每单位费用为 \(c\))。
求最大流的前提下,最小化费用。
考虑 EK 的算法过程,每次找一个最短增广路。这个也一样,不过找的是 \(\sum cost\) 最小的增广路,把 bfs 换成 SPFA 即可。
反向边的 \(cost\) 当然就是原边的 \(cost\) 取反,毕竟反悔就相当于把费用拿回来了。
至于 Dinic,当然也基本同理,但是用的不多。如果遇到 \(-1,0,1\) 这种边权就可能需要了。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 5e3 + 5, O = 5e3 + 5, M = 5e4 + 5;
struct Edge
{
int u, v, w, c, nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, int w, int c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, dis[O], pre[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<int, int> solve(int x, int y)
{
s = x, t = y;
int res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int n, m, s, t;
int main()
{
cin >> n >> m >> s >> t;
int u, v, w, c;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d%d", &u, &v, &w, &c);
flow::addEdge(u, v, w, c);
}
auto ans = flow::solve(s, t);
cout << ans.first << ' ' << ans.second << endl;
return 0;
}
一些例题
费用流本身只是个工具,建图往往是比较困难的部分。
P2053 [SCOI2007] 修车
首先考虑每个人对答案的贡献。假设有 \(k\) 个人选择同一个师傅,师傅维修的时间依次是 \(t_1,t_2,...,t_k\)。
则此时总等待时间为 \(kt_1 + (k-1)t_2 + ... + 2t_{k-1} + t_k\)。这个好难算啊!因为第一个人的贡献还关系到后面有几个人。
那把它反过来不就行了:\(t_k + 2t_{k-1} + ... + (k-1)t_2 + kt_1\)。反正 \(t\) 的顺序自己定,所以总时间就等价于:
然后做一个经典的操作:对每个师傅建 \(n\) 个点,\((j,k)\) 表示第 \(j\) 个师傅、第 \(k\) 次修车,\(k\) 也就是费用系数。
然后每个顾客 \(i\) 就连一下每一个点,边权为 \((1,T_{i,j}\times k)\)。源点向每个顾客连 \((1,0)\) 的边,每个师傅点向汇点也是 \((1,0)\)。
跑费用流即可。输出平均等待时间,除以 \(n\) 就好。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 65, O = 605, M = 1e5 + 5;
int n, m, a[N][N];
int trans(int i, int j)
{
return i * n + j;
}
struct Edge
{
int u, v, w, c, nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, int w, int c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, dis[O], pre[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<int, int> solve(int x, int y)
{
s = x, t = y;
int res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int main()
{
cin >> m >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
int s = 0, t = (m + 1) * n + 1;
for (int i = 1; i <= n; i++)
{
flow::addEdge(s, i, 1, 0);
for (int j = 1; j <= m; j++)
for (int k = 1; k <= n; k++)
{
flow::addEdge(i, trans(j, k), 1, a[i][j] * k);
if (i == n)
flow::addEdge(trans(j, k), t, 1, 0);
}
}
double ans = flow::solve(s, t).second;
ans /= double(n);
printf("%.2lf\n", ans);
return 0;
}
P2050 [NOI2012] 美食节
刚刚那题的加强版,数据范围变大了。
首先,每个菜品 \(p_i\) 个需求,就把边权改为 \((p_i,0)\)。其他就没什么区别了。
算一算复杂度?
点数:\(\mathcal{O}(nm)\)
边数:\(\mathcal{O}(n^2m)\)
EK 的增广轮数:\(\mathcal{O}(p)\)
即使把 SPFA 看成 \(\mathcal{O}(边数)\) 的,总时间复杂度也是 \(\mathcal{O}(n^2mp)\) 的,\(10^8\) 左右。如果你觉得它有希望的话可以尝试一下
怎么优化?观察一下增广的过程,发现很多厨师的点是无用的。具体来讲,每个厨师有用的点一定是一个前缀,因为 \(k\) 越往后费用越高。
于是考虑动态开点 建点。每次增广完之后看看这一轮用了哪个厨师的,就新建一个点。
这样点数就变为了 \(\mathcal{O}(p)\),边数变为了 \(\mathcal{O}(np)\) 的,复杂度得到剧烈 很大优化。放心,可以过的!
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 105, O = 1e5 + 5, M = 1e5 + 5;
int n, m, p[N], a[N][N], cnt[N];
int trans(int i, int j)
{
return i * 801 + j;
}
struct Edge
{
int u, v, w, c, nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, int w, int c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, dis[O], pre[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<int, int> solve(int x, int y)
{
s = x, t = y;
int res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
int j = e[i].u / 801;
cnt[j]++;
for (int i = 1; i <= n; i++)
addEdge(i, trans(j, cnt[j]), 1, a[i][j] * cnt[j]);
addEdge(trans(j, cnt[j]), t, 1, 0);
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
scanf("%d", p + i);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
int s = 0, t = 1e5;
for (int i = 1; i <= n; i++)
{
flow::addEdge(s, i, p[i], 0);
for (int j = 1; j <= m; j++)
{
cnt[j] = 1;
flow::addEdge(i, trans(j, 1), 1, a[i][j]);
if (i == 1)
flow::addEdge(trans(j, 1), t, 1, 0);
}
}
cout << flow::solve(s, t).second << endl;
return 0;
}
P4249 [WC2007] 剪刀石头布
也是类似的模型。难点在于转化。
考虑把满的胜负情况看成一张竞赛图。
然后画几个三元环看看。。发现如果它不是“剪刀石头布”,当且仅当存在一个点入度为 2。
设点 \(u\) 的入度为 \(d_u\)。又因为最终这个竞赛图是两两之间有边的,所以“剪刀石头布”的个数就是
于是问题就变成了最小化后面那坨。
然后就可以自己试试建图。
建图方案
假如给你的矩阵全 2,那么:
对每组 \((u,v)(u\ne v)\),源点向其连 \((1,0)\),它向 \(u\) 和 \(v\) 各连一条 \((1,0)\)。
然后每个 \(u\) 向汇点连 \((1,0),(1,1),(1,2),(1,3),...,(1,n-1)\)。(想想为什么)注意这种连边要保证最优情况下一定是流满一个前缀,也就是费用递增,因此这题可以这样连。
这里就不用对每个 \(u\) 复制 \(n\) 份了,直接连 \(n\) 条就行,因为费用都一样。
如果有非 2 的,\((u,v)\) 就不用建了。然后每个 \(u\) 向汇点连的边要考虑初始入度。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 105, O = N * (N + 1), M = 4 * N * N;
int n, g[N][N], d[N];
int trans(int i, int j)
{
return i * n + j;
}
struct Edge
{
int u, v, w, c, nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, int w, int c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, dis[O], pre[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
void solve(int x, int y)
{
s = x, t = y;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
}
for (int u = 1; u <= n; u++)
for (int v = u + 1; v <= n; v++)
if (g[u][v] == 2)
{
int o = 0;
for (int i = head[trans(u, v)]; i; i = e[i].nxt)
if (e[i].w == 0)
o = e[i].v;
g[u + v - o][o] = 1;
g[o][u + v - o] = 0;
}
}
};
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
scanf("%d", &g[i][j]);
if (g[i][j] == 1)
d[j]++;
}
int s = 0, t = trans(n, n) + 1;
for (int u = 1; u <= n; u++)
for (int v = u + 1; v <= n; v++)
if (g[u][v] == 2)
{
flow::addEdge(s, trans(u, v), 1, 0);
flow::addEdge(trans(u, v), u, 1, 0);
flow::addEdge(trans(u, v), v, 1, 0);
}
for (int u = 1; u <= n; u++)
for (int i = d[u] + 1; i <= n; i++)
flow::addEdge(u, t, 1, i - 1);
flow::solve(s, t);
memset(d, 0, sizeof(d));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (g[i][j] == 1)
d[j]++;
int ans = n * (n - 1) * (n - 2) / 6;
for (int i = 1; i <= n; i++)
{
ans -= d[i] * (d[i] - 1) / 2;
g[i][i] = 0;
}
cout << ans << endl;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
printf("%d%c", g[i][j], " \n"[j == n]);
return 0;
}
P4307 [JSOI2009] 球队收益 / 球队预算
首先根据已经举行的比赛可以确定每个队至少赢了几场。
然后剩下的比赛假设双方都输,然后发现,如果 \(x\) 增加 1,\(y\) 减少 1,变化量是:
这个东西是随胜利场数变多而递增的,于是可以连边了,费用变化量。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N = 5005, O = 6005, M = 1e4 + 5;
int n, m, a[N], b[N], c[N], d[N], cnt[N], ans;
struct Edge
{
int u, v, w, c, nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, int w, int c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, dis[O], pre[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<int, int> solve(int x, int y)
{
s = x, t = y;
int res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
scanf("%d%d%d%d", a + i, b + i, c + i, d + i);
int s = 0, t = n + m + 1, x, y;
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &x, &y);
cnt[x]++, cnt[y]++;
b[x]++, b[y]++;
flow::addEdge(s, i + n, 1, 0);
flow::addEdge(i + n, x, 1, 0);
flow::addEdge(i + n, y, 1, 0);
}
for (int i = 1; i <= n; i++)
{
ans += a[i] * a[i] * c[i] + b[i] * b[i] * d[i];
for (int j = 1; j <= cnt[i]; j++)
{
flow::addEdge(i, t, 1, c[i] + d[i] + 2 * a[i] * c[i] - 2 * b[i] * d[i]);
a[i]++, b[i]--;
}
}
cout << ans + flow::solve(s, t).second << endl;
return 0;
}
P3980 [NOI2008] 志愿者招募
神仙题。
题目说是一个区间加,很不好做,就考虑用一些手段差分掉。
那就可以开始尝试推柿子。
假设有三类志愿者,有四天,覆盖的区间分别是 \([1,3],[3,4],[2,3]\)。那就能列出如下不等式:
不等式经常不好处理,所以强制转成等式:
其中 \(p_i\) 非负。
然后在前后补上空不等式,做个差分:
这下就把区间拆成左右端点了,离答案不远了!
为了方便建图,移一下项:
这个就很明显可以建图了,每个等式为一个点,正号看成入边,负号看成出边。
经过尝试,可以得到一种很好的建图方案:
单个数的边权指的是容量,费用为 0。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int O = 1e3 + 10, M = 2e4 + 5;
int n, m;
struct Edge
{
int u, v;
ll w, c;
int nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, ll w, ll c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, pre[O];
ll dis[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<ll, ll> solve(int x, int y)
{
s = x, t = y;
ll res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int main()
{
cin >> n >> m;
int s = 0, t = n + 2;
int a, l, r, c;
for (int i = 1; i <= n; i++)
{
scanf("%d", &a);
flow::addEdge(s, i, a, 0);
flow::addEdge(i + 1, t, a, 0);
flow::addEdge(i + 1, i, inf, 0);
}
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &l, &r, &c);
flow::addEdge(l, r + 1, inf, c);
}
cout << flow::solve(s, t).second << endl;
return 0;
}
AT_agc034_d [AGC034D] Manhattan Max Matching
一种容易想到的连法是两两点之间连费用,但是边数过多。
考虑拆绝对值。
于是建四个点作为中转点,每个点连四条边就好了。
点击查看代码
// Author: Aquizahv
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int O = 2e3 + 10, M = 1e4 + 5;
int n;
struct Edge
{
int u, v;
ll w, c;
int nxt;
};
namespace flow
{
int pos = 1, head[O];
Edge e[M << 1];
void addEdge(int u, int v, ll w, ll c)
{
e[++pos] = {u, v, w, c, head[u]};
head[u] = pos;
if (!(pos & 1))
addEdge(v, u, 0, -c);
}
int s, t, pre[O];
ll dis[O], val[O];
bool vis[O];
bool spfa()
{
queue<int> q;
q.push(s);
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
val[s] = inf;
vis[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (e[i].w && dis[v] > dis[u] + e[i].c)
{
dis[v] = dis[u] + e[i].c;
val[v] = min(val[u], e[i].w);
pre[v] = i;
if (!vis[v])
{
q.push(v);
vis[v] = true;
}
}
}
}
return dis[t] != inf;
}
pair<ll, ll> solve(int x, int y)
{
s = x, t = y;
ll res = 0, cost = 0;
while (spfa())
{
int u = t, i = pre[t];
while (u != s)
{
e[i].w -= val[t];
e[i ^ 1].w += val[t];
u = e[i].u;
i = pre[u];
}
res += val[t];
cost += dis[t] * val[t];
}
return {res, cost};
}
};
int main()
{
cin >> n;
int n2 = 2 * n;
int s = 0, t = n2 + 1;
int A = n2 + 2, B = n2 + 3, C = n2 + 4, D = n2 + 5;
int x, y, c;
for (int i = 1; i <= n; i++)
{
scanf("%d%d%d", &x, &y, &c);
flow::addEdge(s, i, c, 0);
flow::addEdge(i, A, 10, x + y);
flow::addEdge(i, B, 10, -(x + y));
flow::addEdge(i, C, 10, x - y);
flow::addEdge(i, D, 10, -(x - y));
}
for (int i = n + 1; i <= n2; i++)
{
scanf("%d%d%d", &x, &y, &c);
flow::addEdge(i, t, c, 0);
flow::addEdge(A, i, 10, -(x + y));
flow::addEdge(B, i, 10, x + y);
flow::addEdge(C, i, 10, -(x - y));
flow::addEdge(D, i, 10, x - y);
}
cout << -flow::solve(s, t).second << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号