【构造 思维题】7.12道路建设
题目大意
构造一张点数$n\le 300$的图,使得$1$到$n$的最短路数量恰好为$k$($k\le 1000000007$)
题目分析
法老的原创题,从智商锁那儿来的启发。
但是容易发现 虽然随机图的生成树个数是一个大到可以在模意义下视作随机数的数,但是随机图的最短路数量一般是很少的,想要大量构造大规模最短路条数的图比较困难。
部分分:小质因数分解
譬如“所有质因数大小<10/20”这一类的部分分,可以先内置几张最短路数量的小图,然后再拼接起来
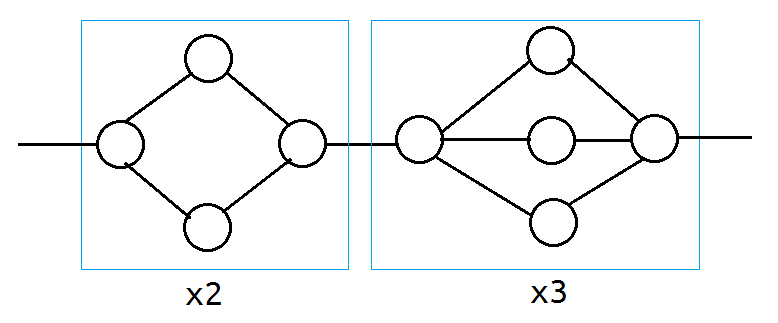
做法一:二进制分解
考虑将$n$二进制分解成$(b_kb_{k-1}\cdots b_1)_2$,也就是$n=\sum\limits_{i=1}^k 2^{i-1}b_i$.
首先考虑最短路为$2^i$的图怎么构造:因为$i\le \log_2 (10^9+7)$,所以将$i$个$\times 2$的零件串在一起即可。
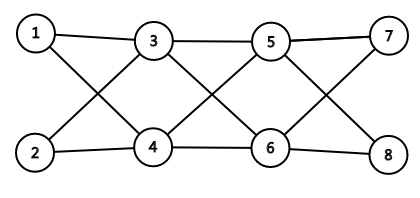
这样类似一个针线状。
接下去的问题是怎么得到$2^i+2^j$的图:一个初步的想法就是把若干个以上的$\times 2^i$零件给“并联”在一起,少的路径通过加点来保持最短路长度不变。但是这个想法的冗余实在太多,例如$(111\cdots 111)_2$的数据吃不消。
比较巧妙的方法是外接一条“并行链”,再通过以上的“放大器”达到终点。因为这个“放大器”实际上有些路径是没用的;而有些路径因为进入的位置不一样,所以可以被多次算进贡献里。
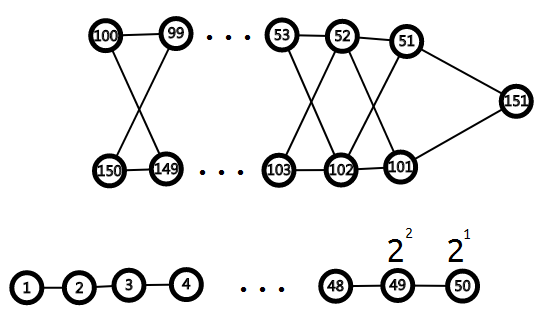
大概长这个样子,还是有点意思的。
1 #include<bits/stdc++.h> 2 #define MO 1000000007 3 const int maxn = 1005; 4 5 int n; 6 7 struct Graph 8 { 9 int n,m; 10 bool mp[maxn][maxn]; 11 12 void output(int det) 13 { 14 for (int p=1; p<=n; p++) 15 for (int t=p+1; t<=n; t++) 16 if (mp[p][t]) printf("%d %d\n",p+det,t+det); 17 } 18 void addedge(int u, int v) 19 { 20 ++m, mp[u][v] = mp[v][u] = true; 21 } 22 void init() 23 { 24 n = 151; 25 for (int i=1; i<50; i++) 26 { 27 addedge(i+50, i+51); 28 addedge(i+50, i+101); 29 addedge(i+100, i+51); 30 addedge(i+100, i+101); 31 addedge(i, i+1); 32 } 33 addedge(51, 151), addedge(101, 151); 34 } 35 }f; 36 int pr[maxn]; 37 bool vis[maxn]; 38 39 int stk[6]; 40 void output() 41 { 42 printf("%d %d\n",f.n,f.m); 43 f.output(0); 44 } 45 int main() 46 { 47 freopen("road.in","r",stdin); 48 freopen("road.out","w",stdout); 49 scanf("%d",&n); 50 f.init(); 51 for (int i=1; i<=50; i++, n>>=1) 52 if (n&1) f.addedge(50-i+1, 50+i); 53 output(); 54 return 0; 55 }
做法二:倍增
考虑以下两种变换:$(n,2n)$,$(n,n+1)$.
第一种变换无非就是把原先的一张图在终点之后又连接一个$\times 2$的零件。
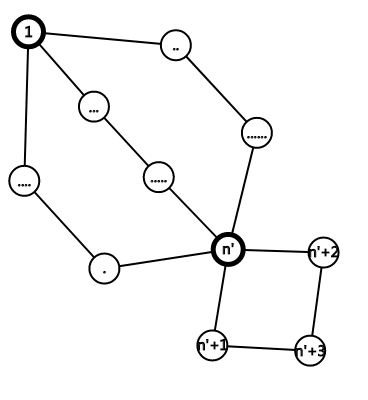
第二种变换也就是再添加$dis+1$(dis为最短路距离)个点,直接完全新建一条通向终点的路径。
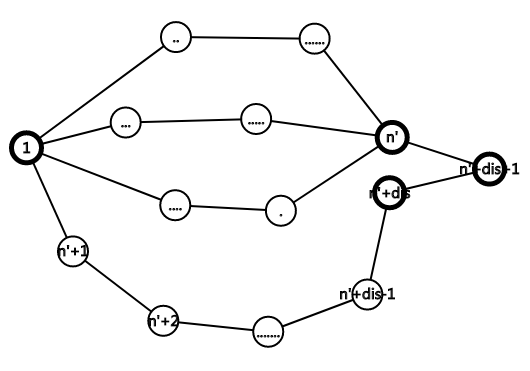
但是如果纯粹这样操作,最坏数据可以卡到400个点左右,而且也没有放在这里的必要了。
分析一下上面这个纯粹的做法,发现我们为时刻能够应对下一次未知操作,浪费了一些节点去时刻保持其性质。
那么我们设定两个“插头节点”,就是为处理下一次$\times 2$操作的节点。
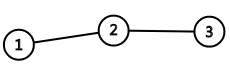
初始是这样的,我们将插头节点定为2,3.
假设有一次$+1$操作,于是在$d=2$的情况下,就新建这样一个路径。
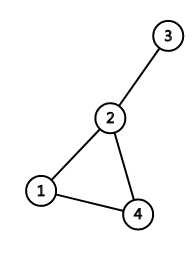
因为插头结点是最接近终点的节点,那么我们新建的路径都连向插头结点。
等等,看到这里有没有意识到一开始把2,3定为插头结点很奇怪?
1到2,3的距离又不相同,难道3这个插头结点在后续过程中不会让其中一条路径不合法?
那么回到初始状态,假设最初的操作是$\times 2$操作:
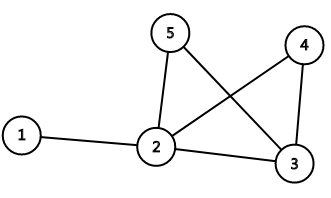
不难发现实际上最初的插头结点设成2,3不过是为了省一个特判,因为无论是在初始状态$\times 2$还是$终止$,最短路径一定是从2连出,而新的插头结点4,5又需要2,3,那么3这个看似不符的插头结点就是没有影响的。
以下是一个中等大小的例子。
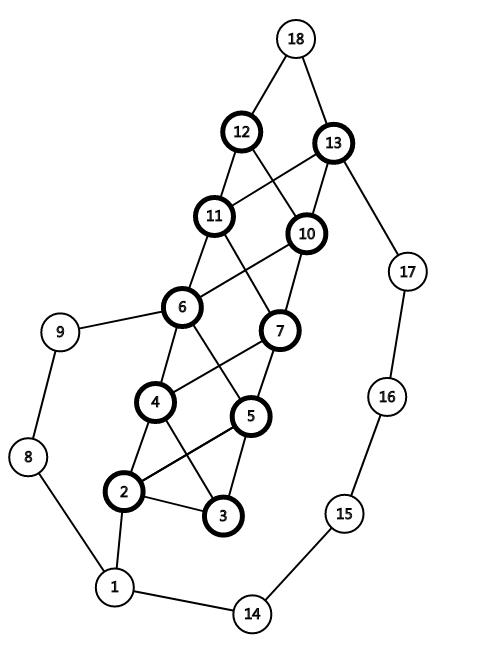
1 #include<bits/stdc++.h> 2 #define MO 1000000007 3 const int maxn = 303; 4 5 int n,x,y,d; 6 7 struct Graph 8 { 9 int n,m; 10 bool mp[maxn][maxn]; 11 12 void output() 13 { 14 for (int p=1; p<=n; p++) 15 for (int t=p+1; t<=n; t++) 16 if (mp[p][t]) printf("%d %d\n",p,t); 17 } 18 void add(int u, int v) 19 { 20 ++m, mp[u][v] = mp[v][u] = true; 21 } 22 void init() 23 { 24 n = 3, add(1, 2), add(2, 3); 25 } 26 }f; 27 28 void deal(int x, int &S, int &T, int &d) 29 { 30 if (x==1) return; 31 else{ 32 if (x&1){ 33 deal(x-1, S, T, d); 34 for (int i=2; i<d; i++) 35 f.add(f.n+i-1, f.n+i); 36 f.add(1, f.n+1), f.add(f.n+d-1, S); 37 f.n += d-1; 38 }else{ 39 deal(x/2, S, T, d); 40 f.add(S, f.n+1), f.add(S, f.n+2); 41 f.add(T, f.n+1), f.add(T, f.n+2); 42 S = f.n+1, T = f.n+2, f.n += 2, ++d; 43 } 44 } 45 } 46 int main() 47 { 48 freopen("road.in","r",stdin); 49 freopen("road.out","w",stdout); 50 scanf("%d",&n); 51 f.init(); 52 x = 2, y = 3, d = 1; 53 deal(n, x, y, d); 54 ++f.n, f.add(x, f.n), f.add(y, f.n); 55 printf("%d %d\n",f.n,f.m); 56 f.output(); 57 return 0; 58 }
END


 浙公网安备 33010602011771号
浙公网安备 33010602011771号