Codeforces Round499-div2

C. Fly

time limit per test：

1 second

memory limit per test：256 megabytes

Description

Natasha is going to fly on a rocket to Mars and return to Earth. Also, on the way to Mars, she will land on $n-2$ intermediate planets. Formally: we number all the planets from $1$ to $n$. $1$ is Earth, $n$ is Mars. Natasha will make exactly $n$ flights: $1\to 2\to \dots n\to 1$.

Flight from $x$ to $y$ consists of two phases: take-off from planet $x$ and landing to planet $y$. This way, the overall itinerary of the trip will be: the $1$-st planet $\to$ take-off from the $1$-st planet $\to$ landing to the $2$-nd planet $\to$ $2$-nd planet $\to$ take-off from the $2$-nd planet $\to$ $\dots$ $\to$ landing to the $n$-th planet $\to$ the $n$-th planet $\to$ take-off from the $n$-th planet $\to$ landing to the $1$-st planet $\to$ the $1$-st planet.

The mass of the rocket together with all the useful cargo (but without fuel) is $m$ tons. However, Natasha does not know how much fuel to load into the rocket. Unfortunately, fuel can only be loaded on Earth, so if the rocket runs out of fuel on some other planet, Natasha will not be able to return home. Fuel is needed to take-off from each planet and to land to each planet. It is known that $1$ ton of fuel can lift off $a_i$tons of rocket from the $i$-th planet or to land $b_i$ tons of rocket onto the $i$-th planet.

For example, if the weight of rocket is $9$ tons, weight of fuel is $3$ tons and take-off coefficient is $8$ ($a_i=8$), then $1.5$ tons of fuel will be burnt (since $1.5\cdot 8=9+3$). The new weight of fuel after take-off will be $1.5$ tons.

Please note, that it is allowed to burn non-integral amount of fuel during take-off or landing, and the amount of initial fuel can be non-integral as well.

Help Natasha to calculate the minimum mass of fuel to load into the rocket. Note, that the rocket must spend fuel to carry both useful cargo and the fuel itself. However, it doesn't need to carry the fuel which has already been burnt. Assume, that the rocket takes off and lands instantly.

Input

The first line contains a single integer $n$ ($2\le n\le 1000$) — number of planets.

The second line contains the only integer $m$ ($1\le m\le 1000$) — weight of the payload.

The third line contains $n$ integers $a_1,a_2,\dots ,a_n$ ($1\le a_i\le 1000$), where $a_i$ is the number of tons, which can be lifted off by one ton of fuel.

The fourth line contains $n$ integers $b_1,b_2,\dots ,b_n$ ($1\le b_i\le 1000$), where $b_i$ is the number of tons, which can be landed by one ton of fuel.

It is guaranteed, that if Natasha can make a flight, then it takes no more than ${10}^9$ tons of fuel.

Output

If Natasha can fly to Mars through $(n-2)$ planets and return to Earth, print the minimum mass of fuel (in tons) that Natasha should take. Otherwise, print a single number $-1$.

It is guaranteed, that if Natasha can make a flight, then it takes no more than ${10}^9$ tons of fuel.

The answer will be considered correct if its absolute or relative error doesn't exceed ${10}^{-6}$. Formally, let your answer be $p$, and the jury's answer be $q$. Your answer is considered correct if $\frac{|p-q|}{max(1,|q|)}\le {10}^{-6}$.

Examples

input

Copy

2
12
11 8
7 5

output

Copy

10.0000000000

input

Copy

3
1
1 4 1
2 5 3

output

Copy

-1

input

Copy

6
2
4 6 3 3 5 6
2 6 3 6 5 3

output

Copy

85.4800000000

Note

Let's consider the first example.

Initially, the mass of a rocket with fuel is $22$ tons.

• At take-off from Earth one ton of fuel can lift off $11$ tons of cargo, so to lift off $22$ tons you need to burn $2$ tons of fuel. Remaining weight of the rocket with fuel is $20$ tons.
• During landing on Mars, one ton of fuel can land $5$ tons of cargo, so for landing $20$ tons you will need to burn $4$ tons of fuel. There will be $16$ tons of the rocket with fuel remaining.
• While taking off from Mars, one ton of fuel can raise $8$ tons of cargo, so to lift off $16$ tons you will need to burn $2$ tons of fuel. There will be $14$ tons of rocket with fuel after that.
• During landing on Earth, one ton of fuel can land $7$ tons of cargo, so for landing $14$ tons you will need to burn $2$ tons of fuel. Remaining weight is $12$ tons, that is, a rocket without any fuel.

In the second case, the rocket will not be able even to take off from Earth.

题意：

 主人公想要遍历n个星球（顺序已给定：1->2->3->...->n->1），求最少的初始带燃料量。输入第一个数字是星球数n，第二个是飞船自重m，接下来两行，每行n个数字：第一行是从第i个星球发射时1kg燃料能支持多少千克的物质升空，第二行是降落到第i个星球时1kg燃料能支持多少千克的物质落地。

思路：

反向思考，列出方程递推即可（附灵魂画师画作一副）

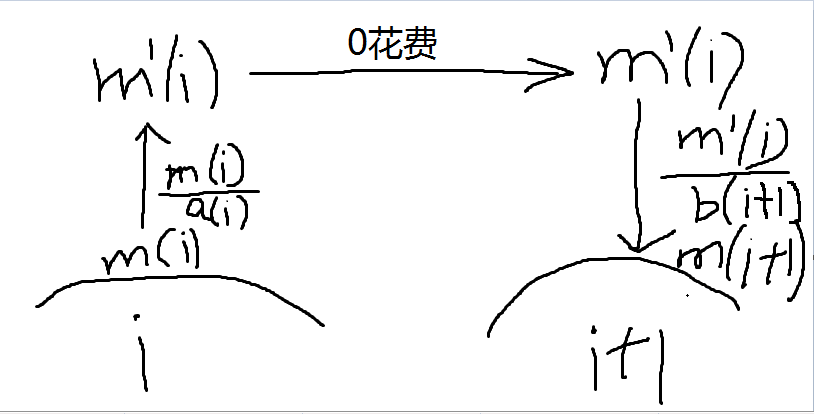
可得方程

m[i-1] = m[i] / ((1 - 1 / a[i-1])*(1 - 1 / b[i]));

 

题解：

根据上面的递推方程递推即可。

注意：

(1)若起飞或落地1kg燃料支持的物质质量小于等于1kg，显然无解，输出-1；

(2)注意题目要求小数位数。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<queue>
#include<cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
double a[1050];
double b[1050];
double c[1050];
int main() {
    int n, m;
    double res;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        if (a[i] <= 1) {
            cout << "-1";
            return 0;
        }
    }
    for (int i = 0; i < n; i++) {
        cin >> b[i];
        if (b[i] <= 1) {
            cout << "-1";
            return 0;
        }
    }
    b[n] = b[0];
    res = m;
    for (int i = n; i >= 1; i--) {
        res = res / ((1 - 1 / a[i-1])*(1 - 1 / b[i]));
    }
    cout << setiosflags(ios::fixed) << setprecision(14) << res - m;
    return 0;
}

 

---

 

 

E.Border

time limit per test：

1 second

memory limit per test：256 megabytes

 

Description

Astronaut Natasha arrived on Mars. She knows that the Martians are very poor aliens. To ensure a better life for the Mars citizens, their emperor decided to take tax from every tourist who visited the planet. Natasha is the inhabitant of Earth, therefore she had to pay the tax to enter the territory of Mars.

There are $\mathrm{nn banknote\; denominations\; on\; Mars:\; the\; value\; of ii-th\; banknote\; is aiai.\; Natasha\; has\; an\; infinite\; number\; of\; banknotes\; of\; each\; denomination.}$

Martians have $\mathrm{kk fingers\; on\; their\; hands,\; so\; they\; use\; a\; number\; system\; with\; base kk.\; In\; addition,\; the\; Martians\; consider\; the\; digit dd (in\; the\; number\; system\; with\; base kk)\; divine.\; Thus,\; if\; the\; last\; digit\; in\; Natasha\text{'}s\; tax\; amount\; written\; in\; the\; number\; system\; with\; the\; base kk is dd,\; the\; Martians\; will\; be\; happy.\; Unfortunately,\; Natasha\; does\; not\; know\; the\; Martians\text{'}\; divine\; digit\; yet.}$

Determine for which values $\mathrm{dd Natasha\; can\; make\; the\; Martians\; happy.}$

Natasha can use only her banknotes. Martians don't give her change.

 

Input

The first line contains two integers $\mathrm{nn and kk (1\le n\le 1000001\le n\le 100000, 2\le k\le 1000002\le k\le 100000) —\; the\; number\; of\; denominations\; of\; banknotes\; and\; the\; base\; of\; the\; number\; system\; on\; Mars.}$

The second line contains $\mathrm{nn integers a1,a2,\dots ,ana1,a2,\dots ,an (1\le ai\le 1091\le ai\le 109) —\; denominations\; of\; banknotes\; on\; Mars.}$

All numbers are given in decimal notation.

Output

On the first line output the number of values $\mathrm{dd for\; which\; Natasha\; can\; make\; the\; Martians\; happy.}$

In the second line, output all these values in increasing order.

Print all numbers in decimal notation.

Examples

 

input

Copy

2 8
12 20

 

output

Copy

2
0 4 

 

input

Copy

3 10
10 20 30

 

output

Copy

1
0 

 

 

Note

 

Consider the first test case. It uses the octal number system.

 

If you take one banknote with the value of $\mathrm{1212,\; you\; will\; get 148148 in\; octal\; system.\; The\; last\; digit\; is 4848.}$

 

If you take one banknote with the value of $\mathrm{1212 and\; one\; banknote\; with\; the\; value\; of 2020,\; the\; total\; value\; will\; be 3232.\; In\; the\; octal\; system,\; it\; is 408408.\; The\; last\; digit\; is 0808.}$

 

If you take two banknotes with the value of $\mathrm{2020,\; the\; total\; value\; will\; be 4040,\; this\; is 508508 in\; the\; octal\; system.\; The\; last\; digit\; is 0808.}$

 

No other digits other than ${\mathrm{0808 and 4848 can\; be\; obtained.\; Digits 0808 and 4848 could\; also\; be\; obtained\; in\; other\; ways.}}^{}$

 

The second test case uses the decimal number system. The nominals of all banknotes end with zero, so Natasha can give the Martians only the amount whose decimal notation also ends with zero.

 

题意

给定n个数字，每个数字可以选取无限次组成一个和，求这个和对k取余可能有多少种结果。

思路

 由Bezout定理，只需要求出所有数字的最大公约数，然后求这个最大公约数有多少个不同的比k小的非负倍数即可。

【Bezout定理(Bézout's identity)：若gcd(a,b)=d，则存在x,y使得ax+by=d；一般地，ax+by是d的整数倍。x,y叫做(a,b)的贝祖系数(Bézout coefficients)，可由扩展欧几里德算法算出】

题解

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<queue>
#include<cmath>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
int gcd(int x, int y) { return y ? gcd(y, x%y) : x; }
int a[100050];
bool tf[100050];
int main() {
    ios::sync_with_stdio(0);
    int n, k, res, tmp;
    res = 0; tmp = 0;
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        a[i] %= k;
        a[1] = gcd(a[1], a[i]);
    }
    while (true)
    {
        tmp = (tmp + a[1]) % k;
        if (tf[tmp] == true) break;
        tf[tmp] = true;
    }
    for (int i = 0; i < k; i++)if (tf[i])++res;
    cout << res << endl;
    for (int i = 0; i < k; i++)if (tf[i])cout << i << ' ';
    return 0;
}