GRPO （Group Relative Policy Optimization ）

Posted on 2025-02-17 19:23 Antel 阅读(633) 评论(0) 收藏举报

GRPO

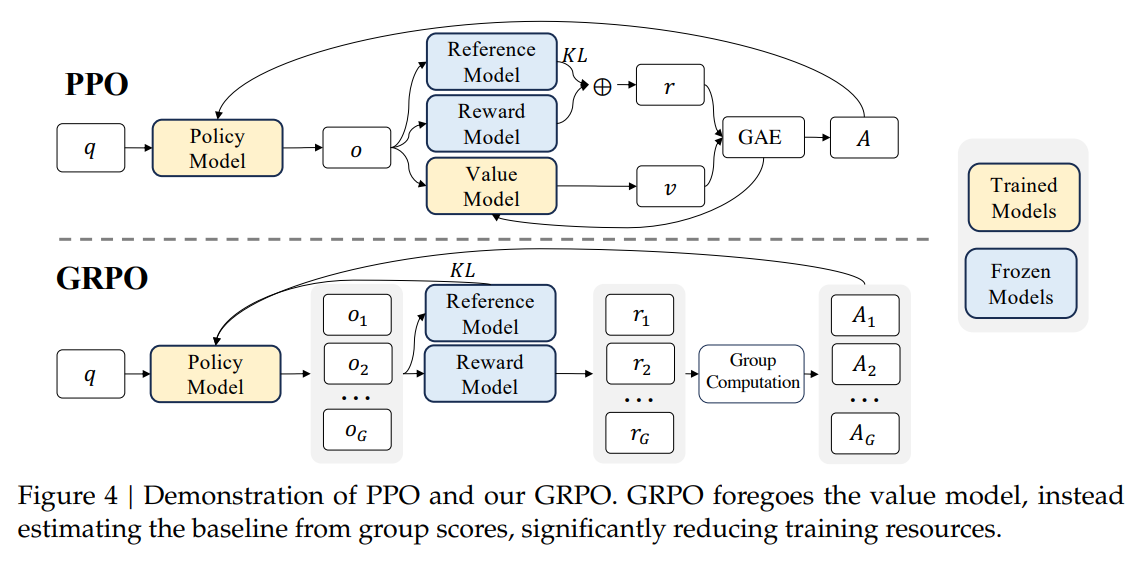
对于每个question q，GRPO从old policy $\pi_{old}$ 采样一组输出 ${o_1, o_2 ...,o_G}$

优化下面的objective以获得新的policy

\[J_{GRPO}(\theta) =E \left [ q \sim P(q), \{o_i \}^G_{i=1} \sim \pi_{\theta_{old}} (O | q) \right ] \\ \frac{1}{G} \sum^{G}_{i=1} \frac{1}{|o_i|} \sum^{|o_i|}_{t=1} \{ \min \left [ \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})}\hat{A}_{i,t}, clip(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})}, 1-\epsilon,1+\epsilon)\hat{A}_{i,t} \right ] -\beta D_{KL} \left [ \pi_{\theta} || \pi_{ref} \right] \} \]

\[D_{KL} \left [ \pi_{\theta}||\pi_{ref} \right] = \frac{\pi_{ref}(o_{i,t} | q,o_{i, <t})}{\pi_{\theta}(o_{i,t} | q,o_{i, <t})} - \log \frac{\pi_{ref}(o_{i,t} | q,o_{i, <t})}{\pi_{\theta}(o_{i,t} | q,o_{i, <t})} -1 \]

其中，$\epsilon$和$\beta$为超参数，$\hat{A}_{i,t}$是advantage。

采用reward modle对这些输出进行打分，生成对应的G的reward $r = {r_1, r_2, ..., r_G}$

对r进行标准化，得到对于每个输出$o_i$结束后的reward标准化advantage $\hat{A}_{i,t}$，并根据上面objective对policy进行优化

\[\hat{A}_{i,t} = \tilde{r_i}=\frac{r_i-mean(r)}{std(r)} \]

概括：根据old policy得到一组输出，计算输出的advantage，据此计算新的policy所需要的优化方向，也就是policy gradient。

所谓policy的old与new，即固定下的策略和正在更新的策略。通过对old policy进行采样，可以进行多步探索，但又通过clip使得更新幅度不过大，保证了数值的稳定性。计算同一组数据在新policy下的概率，得到新policy下的loss，更新新的policy让其相比旧policy能够提升objective。

Loss

https://github.com/huggingface/open-r1/issues/239#issuecomment-2646297851

观察objective，对于某prompt

如果假设每次迭代仅执行一步探索，此时也就是$\pi_{\theta_{old}} = \pi_{\theta}$，用同一个policy进行采样，计算advantage并且更新这个policy

则objective

\[J_{\text{GRPO}}(\theta) = \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \Bigg[ \min \left( \frac{\pi_{\theta}(o_{i,t} \mid q, o_i, < t)}{\pi_{\theta}(o_{i,t} \mid q, o_i, < t)} \hat{A}_{i,t}, \right. \left. \text{clip} \left( \frac{\pi_{\theta}(o_{i,t} \mid q, o_i, < t)}{\pi_{\theta}(o_{i,t} \mid q, o_i, < t)}, 1-\epsilon, 1+\epsilon \right) \hat{A}_{i,t} \right) \\- \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \Bigg] \\ = \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \min \left( \hat{A}_{i,t}, \text{clip}(1,1-\epsilon,1+\epsilon) \hat{A}_{i,t} \right) - \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \right] \\ = \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \min \left( \hat{A}_{i,t}, \hat{A}_{i,t} \right) - \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \right] \\ = \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \hat{A}_{i,t} - \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \right] \\ = \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \hat{A}_{i,t} - \frac{1}{G} \sum_{i=1}^{G} \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \]

Advantage $A$ 不依赖于某个具体token $t$，

\[\frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \hat{A}_{i,t} = \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \hat{A}_i = \hat{A}_i \]

此外，$\hat{A}_t$ 由标准化可知

\[\frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \hat{A}_{t} = 0 \]

因此

\[J_{\text{GRPO}}(\theta) = - \frac{1}{G} \sum_{i=1}^{G} \beta D_{\text{KL}}[\pi_{\theta} \parallel \pi_{\text{ref}}] \]

实际训练loss与KL有关。

梯度

https://arxiv.org/pdf/2402.03300

同样进行一步探索，假设$\pi_{\theta_{\text{old}}} = \pi_{\theta}$

\[J_{\text{GRPO}}(\theta) = \mathbb{E} \big[q \sim p_{\text{sft}}(Q), \{o_i\}_{i=1}^{G} \sim \pi_{\theta_{\text{old}}}(O|q) \big] \\ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \frac{\pi_{\theta}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} | q, o_{i,<t})} \hat{A}_{i,t} - \beta \left( \frac{\pi_{\text{ref}}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta}(o_{i,t} | q, o_{i,<t})} - \log \frac{\pi_{\text{ref}}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta}(o_{i,t} | q, o_{i,<t})} - 1 \right) \right] \]

求梯度，对于中间部分

\[\nabla_{\theta} [\frac{\pi_\theta}{\pi_{\theta_{old}}}A-\beta(\frac{\pi_{ref}}{\pi_\theta}-\log \frac{\pi_{ref}}{\pi_\theta} -1)] \\ = \nabla_{\theta} [\frac{\pi_\theta}{\pi_{\theta_{old}}}A-\beta(\frac{\pi_{ref}}{\pi_\theta}+\log \pi_\theta)] \\ = \frac{\nabla_{\theta}\pi_\theta}{\pi_{\theta_{old}}}A - \beta (-\frac{\pi_{ref}}{\pi_\theta}\frac{\nabla_{\theta}\pi_\theta}{\pi_\theta} + \frac{\nabla_{\theta}\pi_\theta}{\pi_\theta}) \\ = \frac{\nabla_{\theta}\pi_\theta}{\pi_\theta}(A+\beta(\frac{\pi_{ref}}{\pi_\theta}-1)) \\ =(A+\beta(\frac{\pi_{ref}}{\pi_\theta}-1))\nabla_{\theta}\log \pi_\theta \]

得到

\[\nabla_{\theta} J_{\text{GRPO}}(\theta) = \mathbb{E} \big[q \sim p_{\text{sft}}(Q), \{o_i\}_{i=1}^{G} \sim \pi_{\theta_{\text{old}}}(O|q) \big] \\ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \hat{A}_{i,t} + \beta \left( \frac{\pi_{\text{ref}}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta}(o_{i,t} | q, o_{i,<t})} - 1 \right) \right] \nabla_{\theta} \log \pi_{\theta}(o_{i,t} | q, o_{i,<t}) \]

其中，$\nabla_{\theta} \log \pi_{\theta}(o_{i,t} | q, o_{i,<t})$是policy采样logits梯度，而梯度系数（Gradient Coefficient)为

\[GC_{GRPO}(q,o,t,\pi_{\theta_{rm}}) = \hat{A}_{i,t} + \beta \left( \frac{\pi_{\text{ref}}(o_{i,t} | q, o_{i,<t})}{\pi_{\theta}(o_{i,t} | q, o_{i,<t})} - 1 \right) \]

实现

https://github.com/huggingface/trl

https://github.com/huggingface/trl/blob/main/trl/trainer/grpo_trainer.py

trl中关于gpro的实现

def compute_loss(self, model, inputs, return_outputs=False, num_items_in_batch=None):
    
	...
    
    # Compute the KL divergence between the model and the reference model
    ref_per_token_logps = inputs["ref_per_token_logps"]
    per_token_kl = torch.exp(ref_per_token_logps - per_token_logps) - (ref_per_token_logps - per_token_logps) - 1

    # x - x.detach() allows for preserving gradients from x
    advantages = inputs["advantages"]
    per_token_loss = torch.exp(per_token_logps - per_token_logps.detach()) * advantages.unsqueeze(1)
    per_token_loss = -(per_token_loss - self.beta * per_token_kl)
    loss = ((per_token_loss * completion_mask).sum(dim=1) / completion_mask.sum(dim=1)).mean()

    ...

    return loss

方法来自一步探索，

有$\pi_{\theta_{\text{old}}} = \pi_{\theta}$

将objective转成loss

代码中

per_token_loss = torch.exp(per_token_logps - per_token_logps.detach()) * advantages.unsqueeze(1)

torch.exp(per_token_logps - per_token_logps.detach())的值恒为1，对应$ \frac{\pi_\theta}{\pi_{\theta_{old}}}$，保留以便梯度传播。

刷新页面返回顶部

Antel

公告