树的直径
树的直径
树中最远的两个节点之间的距离或者路径被称为树的直径。
树的直径一般有两种写法,时间复杂度都为O(n)。
树形DP
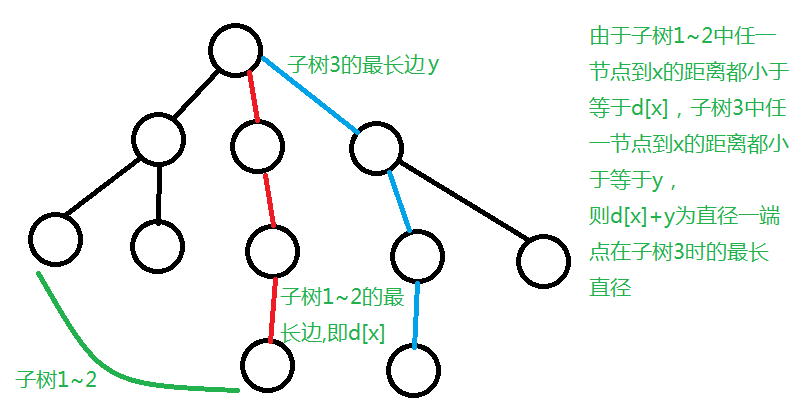
以1号节点为根,d[x]表示从x节点出发可达的最远距离,f[x]表示过x节点的最长路径长度。
对于每个x,扫描到x的第i个子树,d[x]储存了从x到1~i-1的子树的点的最远距离,由这个最远距离加上x到第i个子树中的节点的最远距离,则为x中从i子树的节点出发可得到的最长距离,即可更新f[x]。
void dp(int x)
{
vis[x]=1;
for(int i=tail[x];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(vis[v]) continue;
DP_Tree(v,u);
f[x]=max(f[x],d[x]+d[y]+w);
d[x]=max(d[x],d[y]+w);
}
}
DFS或BFS
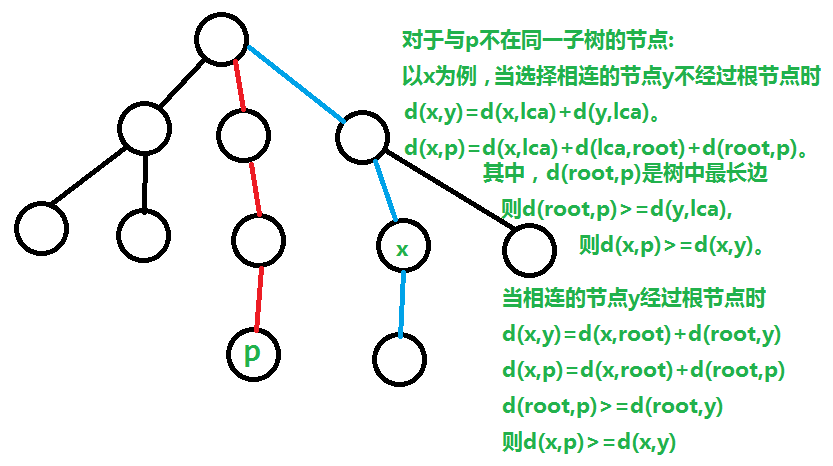
1.从任意节点出发,通过DFS或BFS求出与出发点距离最远的点p。
2.以p为根,通过DFS或BFS求出与p距离最远的点q,pq间距离即为直径。
void dfs(int x)
{
vis[x]=1;
for(int i=tail[x];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(vis[v]) continue;
d[v]=d[x]+w;
if(d[v]>d[ans]) ans=v;
dfs(v);
}
}
int main()
{
dfs(1)
int p=ans;
memset(d,0,sizeof(d));
dfs(p);
int q=ans;
printf("%d",d[q]);
}
巡逻
在一个地区有 n 个村庄,编号为1,2,…,n。
有 n-1 条道路连接着这些村庄,每条道路刚好连接两个村庄,从任何一个村庄,都可以通过这些道路到达其他任一个村庄。
每条道路的长度均为1个单位。
为保证该地区的安全,巡警车每天都要到所有的道路上巡逻。
警察局设在编号为1的村庄里,每天巡警车总是从警局出发,最终又回到警局。
为了减少总的巡逻距离,该地区准备在这些村庄之间建立 K 条新的道路,每条新道路可以连接任意两个村庄。
两条新道路可以在同一个村庄会合或结束,甚至新道路可以是一个环。
因为资金有限,所以 K 只能为1或2。
同时,为了不浪费资金,每天巡警车必须经过新建的道路正好一次。
编写一个程序,在给定村庄间道路信息和需要新建的道路数的情况下,计算出最佳的新建道路的方案,使得总的巡逻距离最小。
输入格式
第一行包含两个整数 n 和 K。
接下来 n-1 行每行两个整数 a 和 b,表示村庄 a 和 b 之间有一条道路。
输出格式
输出一个整数,表示新建了 K 条道路后能达到的最小巡逻距离。
数据范围
3≤n≤100000,
1≤K≤2,
1≤a,b≤n
输入样例:
8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6
输出样例:
输出样例:
11
刚开始我们一共要走的长度是:
路径总长度=2∗(n−1)n是这棵树上的节点个数。
因为对于每一个点而言,我们必须要走两次。 (你可以认为就像是DFS搜索一样)
第一次访问这个点,也就是进入这个点。
第二次访问这个点,也就是离开这个点。
假如说我们之前的树,它的树的直径长度是L,那么经过我们第一轮路径增加过后。
路径总长度−L+1,即少走一遍直径多走一条路。
第二条边:
因为第一条边之后,树中出现了环,我们无法保证第二条边构建的环与第一条边不重合。
如果不重合,则和单独求两次直径无差别。
如果重合:
我们第一次的操作,等于直径上的边只进不出。
第二次操作等于将整段重合的边从树上删除,设重合的长度为l,即\(ans-l\)。
但由于每条边都必须被经过,则我们在删除边得到最小的答案后,还需要额外将这一段边进入退出一次,则\(ans+2*l\),最后即\(ans+l\),导致ans减去直径后还增加了重合的长度。
设直径为d,则\(ans-d+l=ans-(d-l)\),由于每增加一条重合的边,都会使总长度-1+2,则会让减去的部分+1-2,即-1,所以可以直接将重合的部分重新赋值为-1。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int ans,n,k,p,te=1;
int d[N],f,tail[N],pre[N];
struct e_
{
int v,w,pre;
}e[N*2];
inline void add(int u,int v,int w)
{
e[++te]=(e_){v,w,tail[u]};
tail[u]=te;
}
void dfs1(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(v==fa) continue;
d[v]=d[u]+w;
if(d[v]>d[p]) p=v;
dfs1(v,u);
}
}
void dfs2(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(v==fa) continue;
pre[v]=i;
d[v]=d[u]+w;
if(d[v]>d[p]) p=v;
dfs2(v,u);
}
}
void change(int p)
{
int x=pre[p];
if(!x) return;
e[x].w=e[x^1].w=-1;
change(e[x^1].v);
}
void dp(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(v==fa) continue;
dp(v,u);
f=max(f,d[u]+d[v]+w);
d[u]=max(d[u],d[v]+w);
}
}
int main()
{
scanf("%d %d",&n,&k);
ans=2*(n-1);
for(int i=1,u,v;i<n;++i)
{
scanf("%d %d",&u,&v);
add(u,v,1);
add(v,u,1);
}
dfs1(1,0);
memset(d,0,sizeof(d));
dfs2(p,0);
ans-=d[p]-1;
if(k==2)
{
change(p);
memset(d,0,sizeof(d));
dp(1,0);
ans-=f-1;
}
printf("%d",ans);
}
树网的核
设T=(V, E, W) 是一个无圈且连通的无向图(也称为无根树),每条边带有正整数的权,我们称T为树网(treenetwork),其中V, E分别表示结点与边的集合,W表示各边长度的集合,并设T有n个结点。
路径:树网中任何两结点a,b都存在唯一的一条简单路径,d(a,b)表示以a,b为端点的路径的长度,它是该路径上各边长度之和。
我们称d(a,b)为a,b两结点间的距离。
一点v到一条路径P的距离为该点与P上的最近的结点的距离:d(v,P)=min{d(v,u),u为路径P上的结点}。
树网的直径:树网中最长的路径称为树网的直径。
对于给定的树网T,直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距ECC(F):树网T中距路径F最远的结点到路径F的距离,即:ECC(F)=max{d(v,F),v∈V}
任务:对于给定的树网T=(V, E,W)和非负整数s,求一个路径F,它是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过s(可以等于s),使偏心距ECC(F)最小。
我们称这个路径为树网T=(V,E,W)的核(Core)。
必要时,F可以退化为某个结点。
一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
输入格式
包含n行: 第1行,两个正整数n和s,中间用一个空格隔开,其中n为树网结点的个数,s为树网的核的长度的上界,设结点编号依次为1, 2, …, n。
从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。
例如,“2 4 7”表示连接结点2与4的边的长度为7。
所给的数据都是正确的,不必检验。
输出格式
只有一个非负整数,为指定意义下的最小偏心距。
数据范围
n≤500000,s<231
输入样例:
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出样例:
5
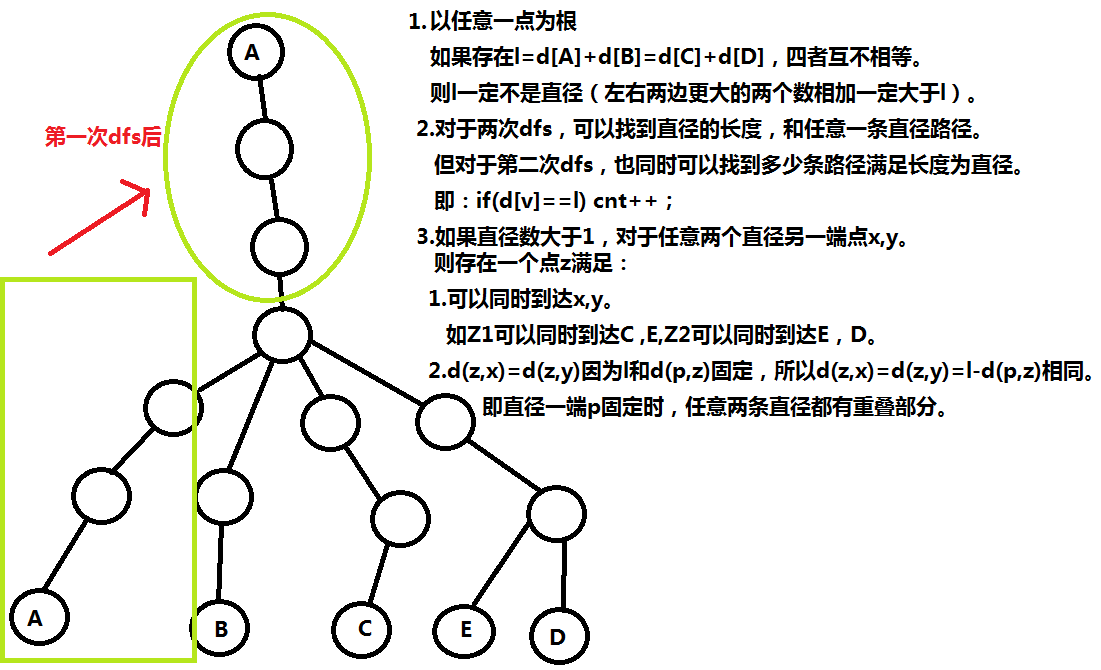
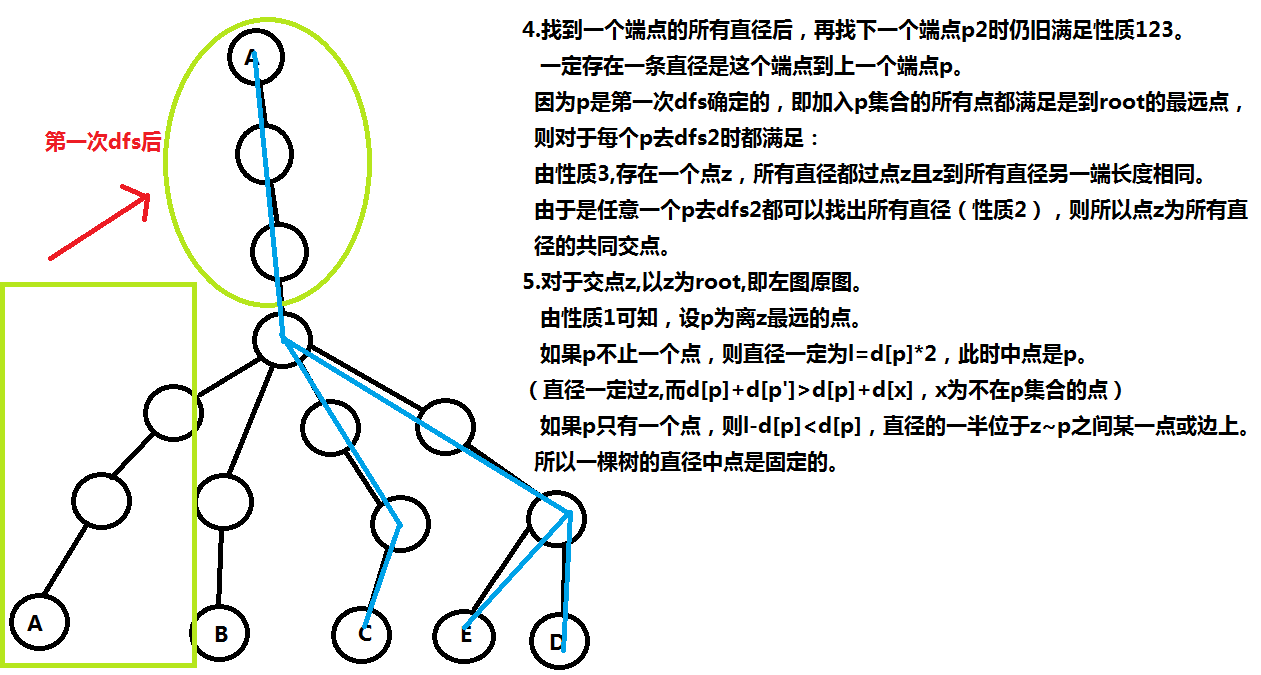
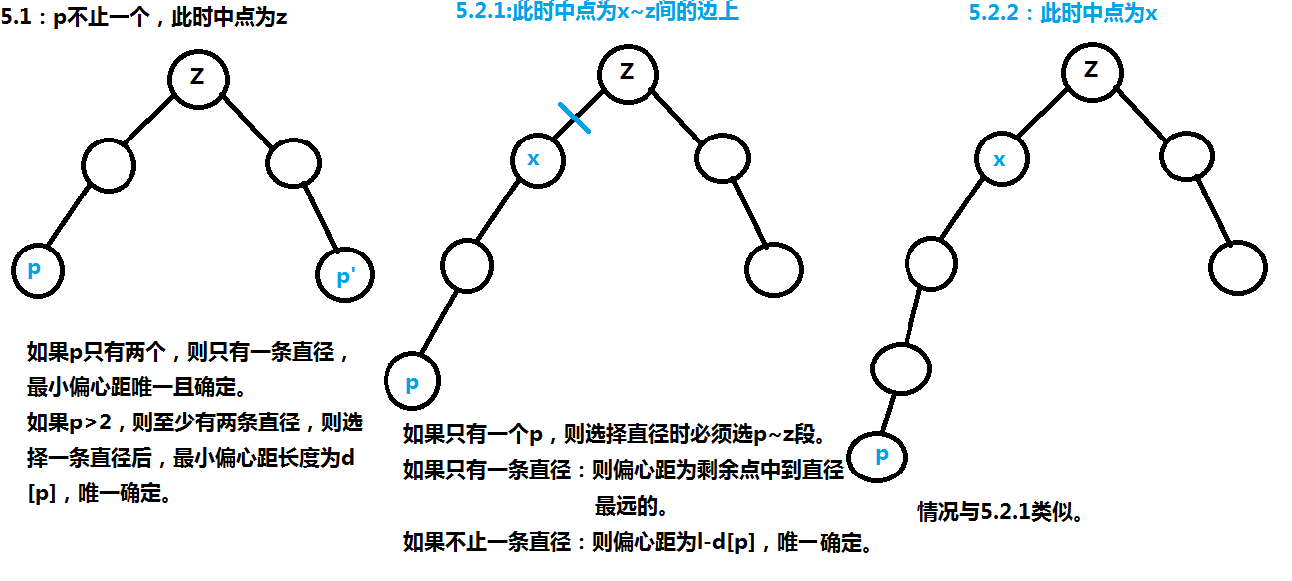
假设z为所有直径交点,以z为根去dfs整棵树处理每个点到z的距离d,因为直径一定过z点,所以离z点最远的点一定是直径的端点之一,假设离z最远的点为p:
如果p>2个,则选择一条直径(d[p1],d[p2])后,还会剩至少一个d[p3],d[p3]>d[x],x是p之外的任意一点,所以这个时候偏心距应该是d[p3]。
如果p=2个,则只有一条直径,偏心距肯定是唯一确定的。
如果p=1个,则直径可以分成p—z段和z—q段,无论怎么选直径一定会把p—z段选上去,因为p—z是距离最大的,z—q段长度和其余长度相加一定会小于p—q段长度。
如果q只有一个,则只有一条直径,则偏心距肯定是唯一确定的。
如果q不止一个,则直径至少有两条,选择一条直径(d[p],d[q1])后,至少还会剩一段d[q2]满足d[q2]>d[x],x是除p,q外的任意一点,因为如果d[x]>d[q2],那直径就应该是p—x而不是p—q了,所以上式一定成立,此时偏心距应该是d[q2],也是唯一确定的。
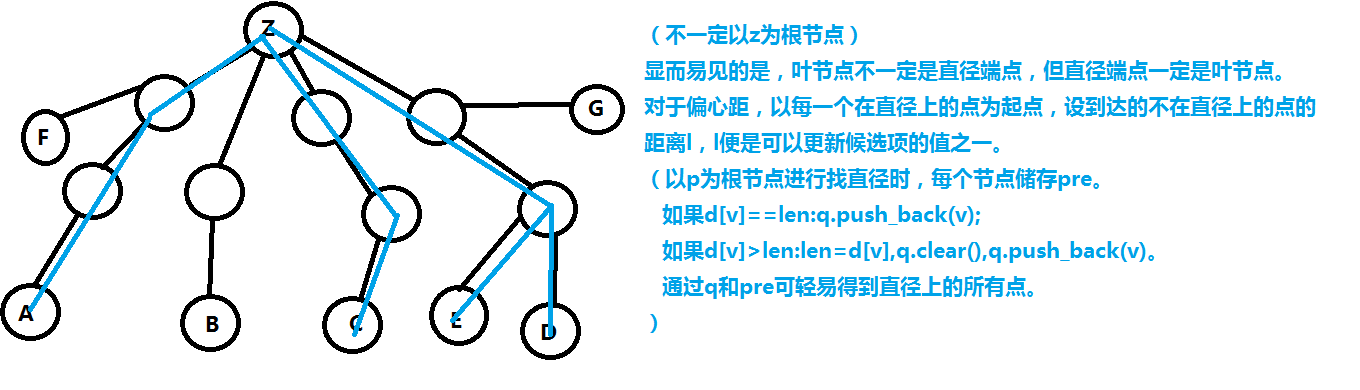

以上是个人想法,下面放yxc老师的正解:
(二分,树的直径,贪心,树的遍历) O(NlogS)
题目中说所有直径的中点均重合。
偏心距也有类似的性质:不管从哪条直径来求最小偏心距,答案都是唯一的。
因此我们可以先找出任意一条直径,这里可以用两次找最长路的方式:
任选一点作为起点,找出距离起点的最远点 u;
再找出距离 u 最远的点 v,则 u和v之间的路径就是树的一条直径。
枚举最小偏心距,判断在直径上是否存在一段长度不超过s的路径,使得其余所有点到路径的距离小于等于枚举的值。
如果偏心距等于d是满足的,那么当偏心距大于d时也一定可以满足,因此我们可以通过二分来枚举。
接下来在直径上找到与 u 的距离不超过 mid 的前提下,距离u最远的节点,作为节点 p。类似地,在直径上找到与 v 的距离不超过 mid 的前提下,距离 v 最远的节点,作为节点 q。
(以u,v为端点距离不超过mid的直径)
根据直径的最长性,任何从u,p之间分叉离开直径的子树,其最远点与 p 的距离都不会比 u 更远。所以 p, q就是在满足直径两侧的那部分节点偏心距不超过 mid 的前提下,尽量靠近树网中心的节点。
(如果其最远点g的距离离p比u更远,则有g-z>u-z,则直径应该是g-p而非u-p)
接下来判断 p, q 之间的距离是否不超过 s,以及p, q之间的所有点到其他所有点的最短距离是否不超过mid即可。时间复杂度
假设所有边长的总和是S,树中节点数是N,则我们一共会二分logS 次,每次判断需要O(N) 的时间,因此总时间复杂度是 O(NlogS)。
如何克服TLE:
1.储存直径所过的点以及长度时,用\(int q[N],qv[N]\)数组代替\(deque<t_>q\)
2.快读代替scanf
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,s,tq,te,p,d[N],dis[N],tail[N],pre[N],qq[N];
bool vis[N];
struct e_
{
int v,w,pre;
}e[N*2];
int q[N],qv[N];
inline void add(int u,int v,int w)
{
e[++te]=(e_){v,w,tail[u]};
tail[u]=te;
}
void bfs1(int x)
{
p=0;
int l=0,r=0;
qq[0]=x;
d[x]=0;
while(l<=r)
{
int u=qq[l++];
vis[u]=1;
if(d[u]>d[p]) p=u;
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(vis[v]) continue;
vis[v]=1;
d[v]=d[u]+w;
qq[++r]=v;
}
}
}
void bfs2(int x)
{
p=0;
int l=0,r=0;
qq[0]=x;
d[x]=0;
while(l<=r)
{
int u=qq[l++];
vis[u]=1;
if(d[u]>d[p]) p=u;
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(vis[v]) continue;
pre[v]=u;
vis[v]=1;
d[v]=d[u]+w;
qq[++r]=v;
}
}
}
bool check(int x)
{
int l=1,r=tq;
while(++l<=r&&qv[1]-qv[l]<=x);
while(--r&&qv[r]<=x);
//l-1,r+1是实际满足条件的点
l--;r++;
if(r<=l) return true;
if(qv[l]-qv[r]>s) return false;
//r-1=l时,正好整条直径左右都满足条件
for(int i=l;i<=r;++i)
if(dis[i]>x) return false;
return true;
}
inline int read()
{
char dd=getchar();
int res=0;
while(dd<'0'||dd>'9') dd=getchar();
while(dd<='9'&&dd>='0') res=(res<<1)+(res<<3)+dd-'0',dd=getchar();
return res;
}
int main()
{
n=read();
s=read();
for(int i=1,u,v,w;i<n;++i)
{
u=read();v=read();w=read();
add(u,v,w);
add(v,u,w);
}
bfs1(1);
memset(vis,0,sizeof(vis));
bfs2(p);
while(p) q[++tq]=p,qv[tq]=d[p],p=pre[p];
memset(vis,0,sizeof(vis));
for(int i=1;i<=tq;++i) vis[q[i]]=1;
for(int i=1;i<=tq;++i)
{
p=0;
bfs1(q[i]);
dis[i]=d[p];
}
int l=0,r=2e9;
while(l<r)
{
int m=(l+r)/2;
if(check(m)) r=m;
else l=m+1;
}
printf("%d",r);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号