GNN(图)笔记

图的基本概念不再详细描述

有顶点（node, V）、边（edge, E），这里还有一个全局属性（global, U），但不知道具体表示什么

边分为无向的边和有方向的边

 

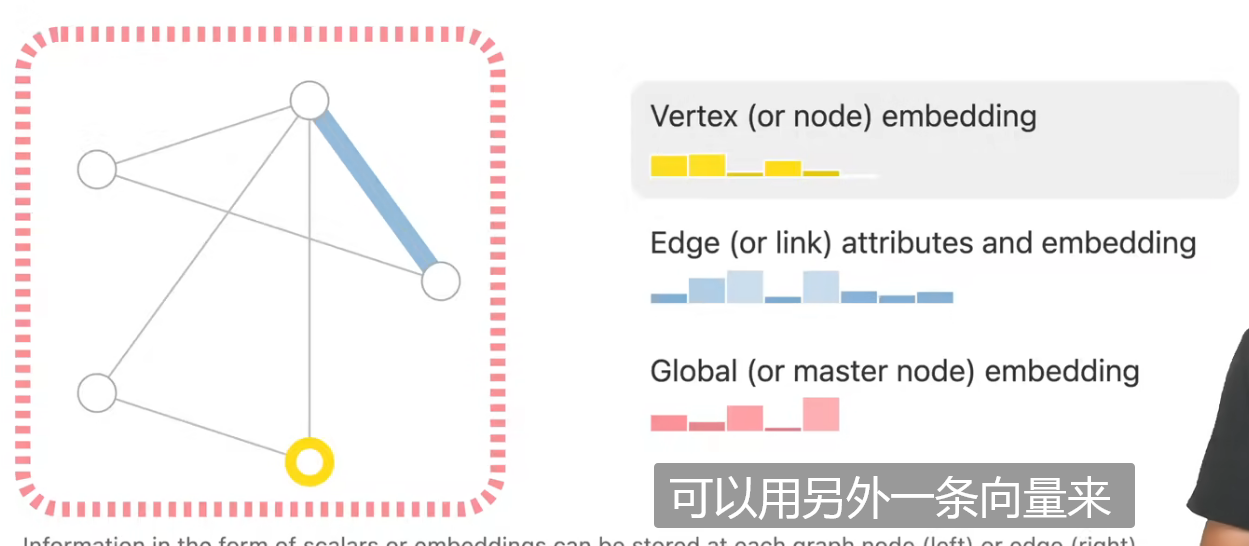
 三者都是通过向量来表示（embedding）

 

将图像表示成图的方法：一个像素是一个节点

下图左边是原图，中间是邻接矩阵，右边是图

 

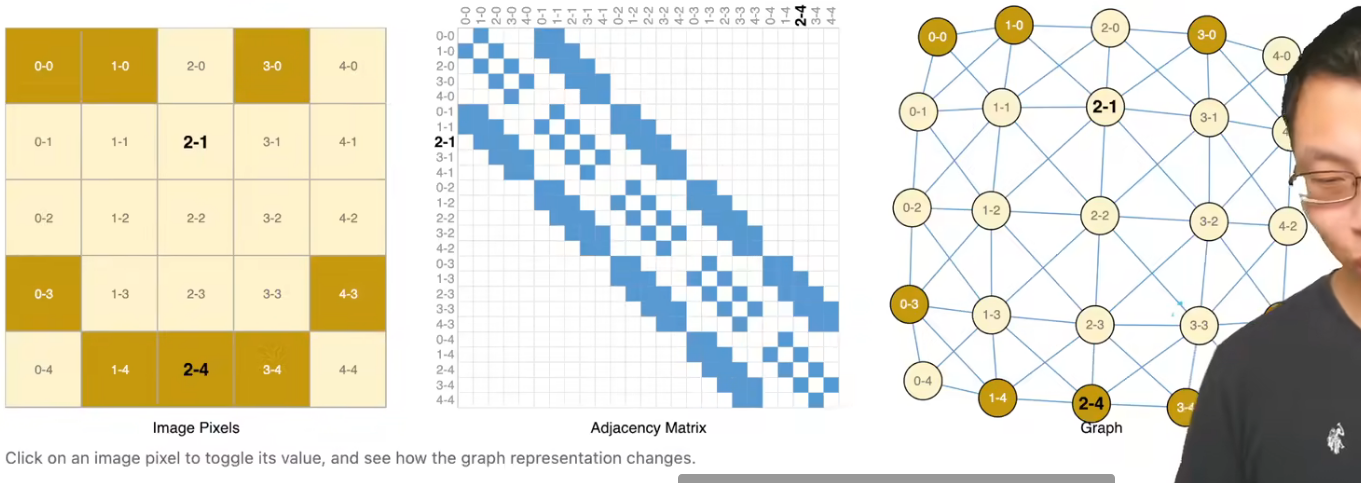
文本则需要用有向边来表示（类似链表），一个顶点表示一个词

 

 

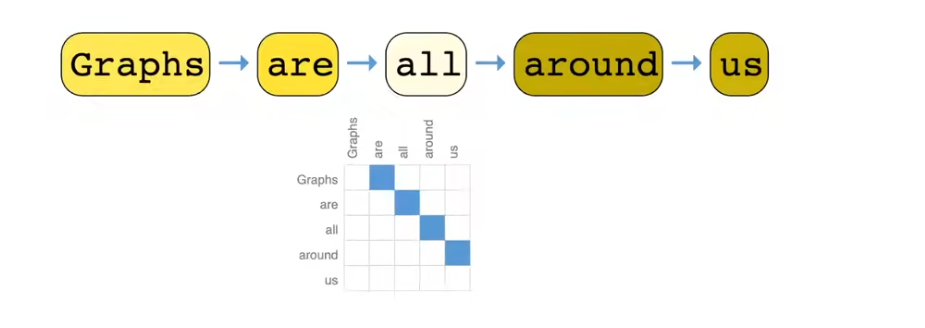
除此以外还有例如有机分子，人物社交网络，比赛赛程，论文之间的引用等都可以用图表示

 

以上是用图表示各类数据的方法，下面讲在图上可以定义什么样的问题：

主要从三个层面来分：图层面、顶点层面、边层面

 

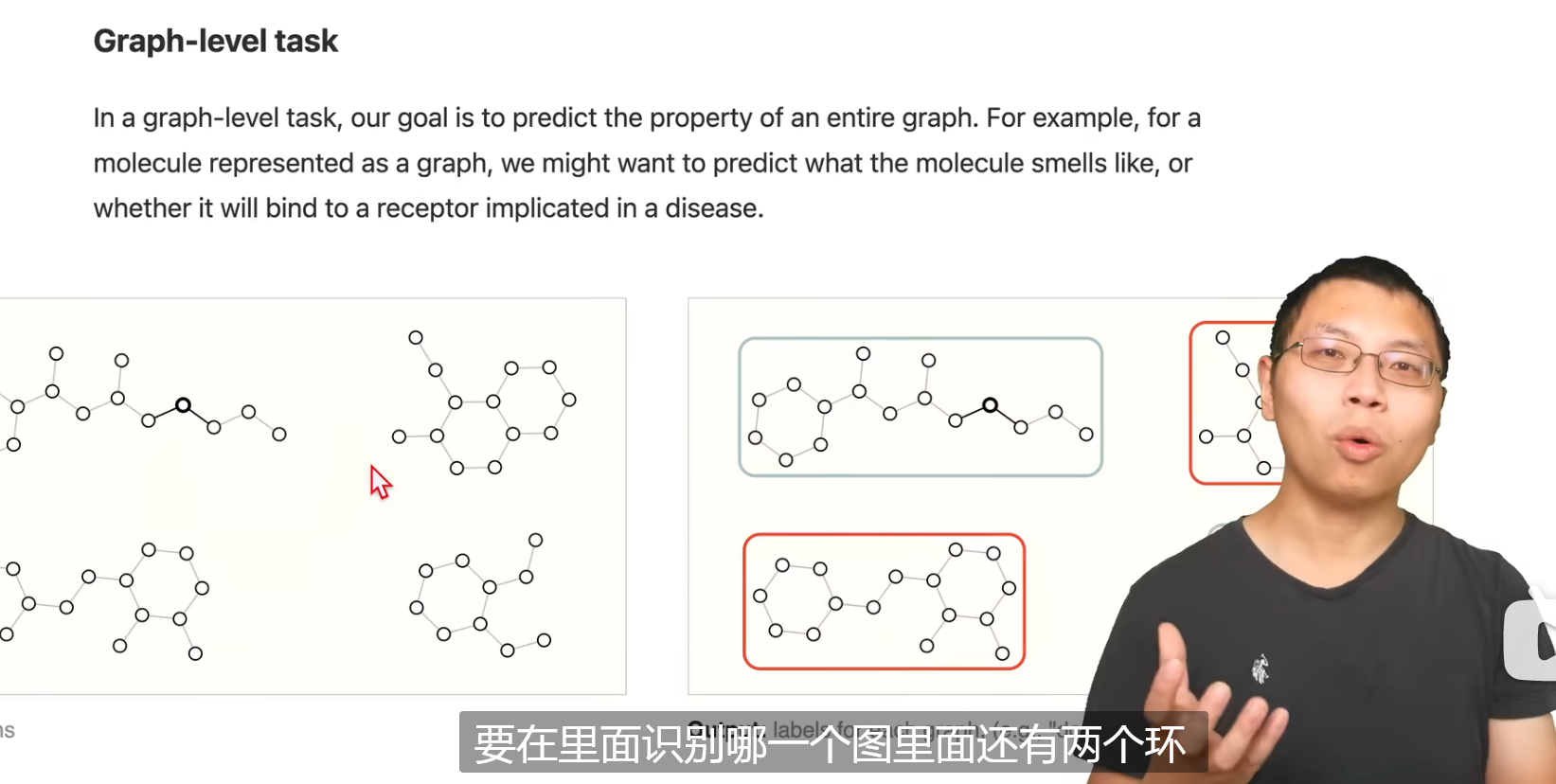
 上图是图层面的一个简单例子，左边是数据集，任务是识别哪些样本中含有两个环。就是分类任务，当然实际上这个任务比较简单，不用机器学习，写一段正常 代码也能做出来

 

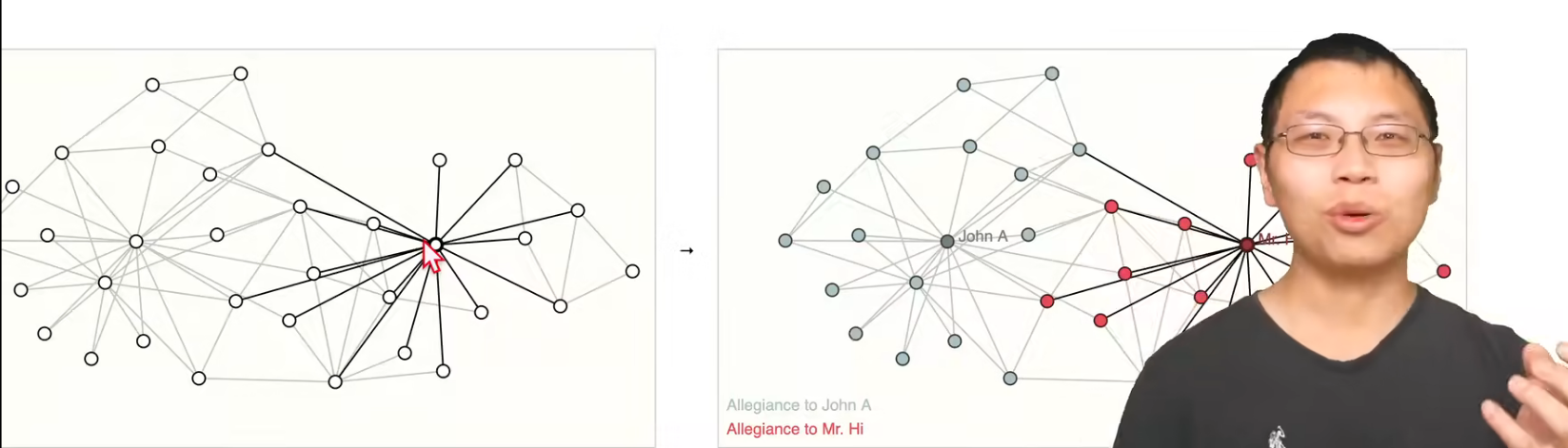
 上图是节点的分类，该图中有两个核心节点，任务是将两个核心节点分裂以后，判断其余所有点属于哪个核心点的阵营

 

 这个是边的任务，首先将一张图片通过语义分割提取人物，然后判断人物之间是什么样的关系

 

在神经网络中使用图的挑战：

一个关键问题是如何表示图，使得它与神经网络兼容

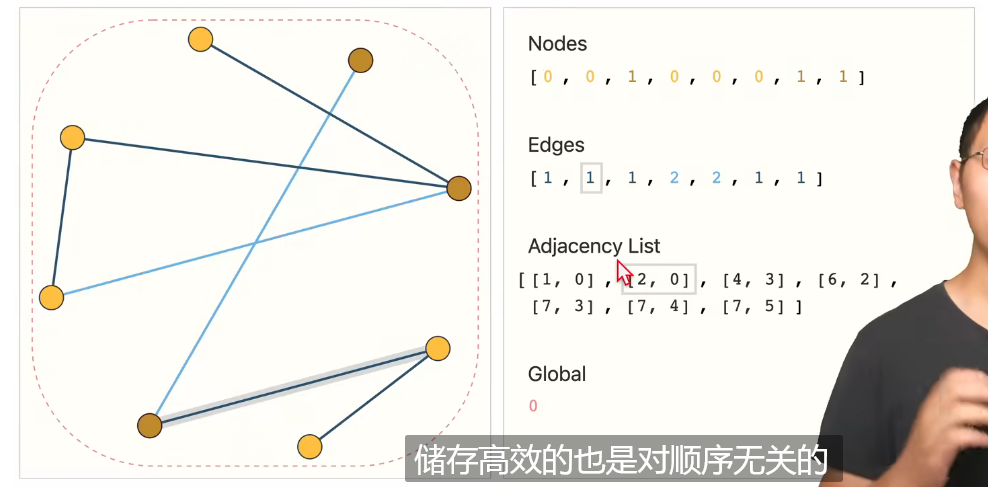
图上共有四种信息，分别是顶点、边、全局以及连接性。前三种是属性，注意即便是边也是边上的属性。最后一条才是边的连接性，也就是一条边具体连着哪两个点。前三者比较好办，直接embedding用向量来表示即可，第四种比较麻烦，一个常见的办法是邻接矩阵。但神经网络处理向量是没问题的，表示连接性的这个矩阵理论上也没问题，但实际中这个邻接矩阵通常是非常大的，虽然可以用稀疏矩阵的方法来存储矩阵，但稀疏矩阵很难在GPU上高效运算。此外，邻接矩阵的表示是行、列顺序无关的，要保证同一个图所有可能的邻接矩阵表示方法输入神经网络后的结果是一样的比较难。为解决这个问题提出以下方法储存图，用一个标量或者一个向量来表示顶点和边，然后用一个顺序无关的列表来表示连接性，但这个地方我没看懂为什么这么多的顶点只有0，1两种表示方法

 

 

 

Graph Neural Networks

定义：GNN是一个对图上所有的属性（顶点、边、全局上下文）进行的优化的变换，这个变化可以保持图的对称信息，及对图的顶点进行另外一种排序后，最终结果不变。注意，这个所谓的排序是表示每一种属性的那个列表内的排序，图的结构即连接性是不变的。

此处用一个信息传递神经网络（message passing neural network）框架来处理图

GNN网络的输入是一个图，输出也是一个图，GNN网络在不改变连接性的前提下对属性进行变换

 

最简单的GNN

 

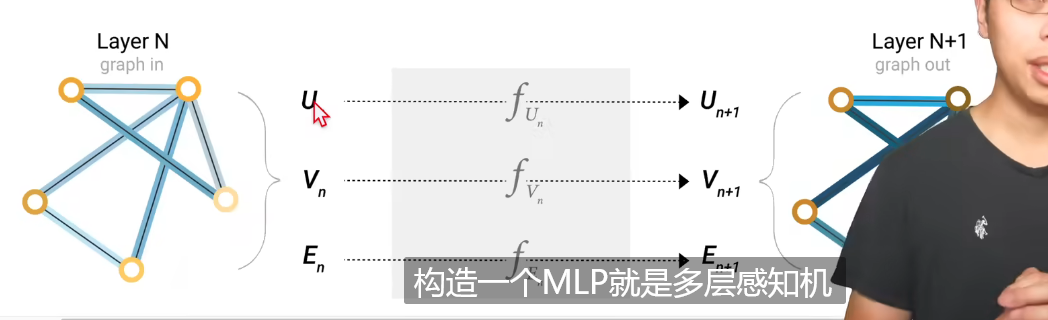
 对于顶点向量、边向量、全局向量分别构造一个MLP，该MLP的输入与输出大小相同，这三个MLP组成一个GNN的层，在这一层中同时更新三个属性的向量表示，但图的结构没有发生变化。可以把这个层多叠加几次，构造一个比较深一点的GNN

 

GNN如何做预测

以上所述的GNN结构可以作为隐藏，那么在最后一层如何输出结果？如果是一个二分类问题，我们对每一个输出的顶点向量表示输入到输出维度为2的全连接层，然后再加一个softmax即可，多分类就是输出为n的全连接层，回归就是输出为1的全连接层。注意，无论有多少个顶点，都共享最后的这一个全连接层。

汇聚（pooling）：有些情况下我们会只有边的向量表示而没有顶点的，那么对顶点的预测结果就是与他有关的边的向量+全局向量。同理，如果没有边的向量或者没有全局的向量也是用已有的东西加起来

下图为一个完整端到端的GNN：输入一个图，组成GNN层，最后输出一个保持了图结构的输出，但其中的属性发生了变换。最后看你要什么样的输出添加一个输出层，如果还缺失什么信息的话再添加汇聚层。最终得到输出Y

 

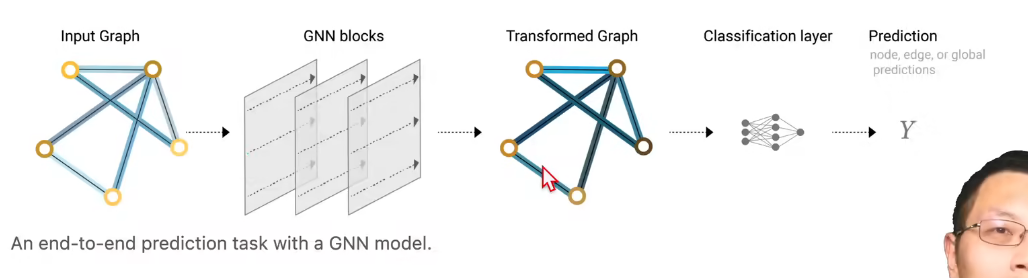
 上述结构有很大的局限性，即每个属性是通过自己的MLP单独考虑的（上图中的GNN blocks），并没有使用到图的结构信息，也就是说连接性那一部分东西没用到

 

下面我们看看如何把图的连接性信息尽早的放入到模型中去考虑，使用的技术是信息传递（passing message）

 之前我们在更新一个顶点时，是直接使用MLP处理该顶点的向量，现在我们在处理一个顶点时把和他有关系的顶点的向量都加上（汇聚），再MLP

原博主认为这个和卷积有一点点像（确实，卷积也是把中心点和周围有关系的加起来），但是李沐指出卷积的3*3的9个窗口里，每个窗口都有自己的权重，最终算的是加权和，而这里就是直接加起来，并没有权重。卷积中的多输入和输出通道对应的是MLP过程，所以通道机制还是保留了。卷积网络在逐渐加深的过程中，节点能够看到距离很远的点的信息，GNN也是如此

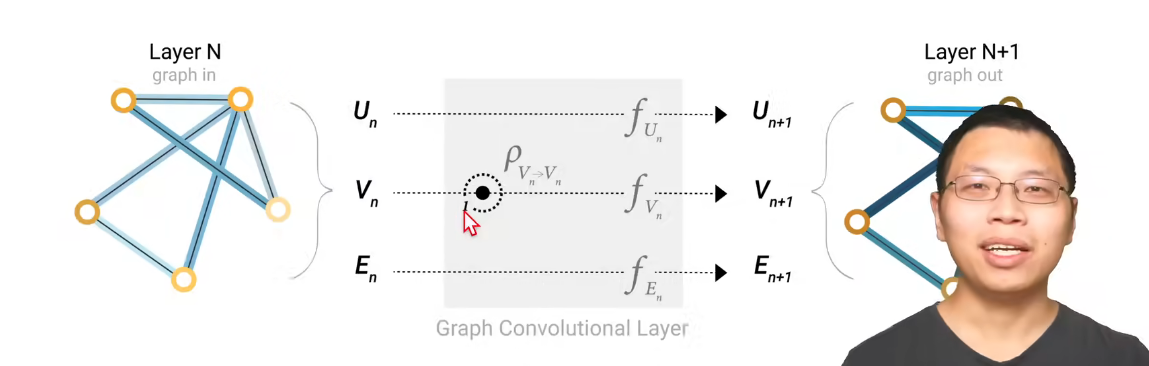
之前讲过，如果有信息缺失我们在模型输出端进行汇聚，但其实这件事可以比较早的做

也就是说如果把顶点的信息传递给边的话，在边上加上相邻顶点的向量即可，如果顶点和边的向量维度不同就投影一次。同理，边的信息也可以还给顶点，如下图所示。那么相当于在边上汇聚了顶点的信息，又把带有边的信息汇聚回了顶点

这里的汇聚可以选择相加，也可以选择concat

 

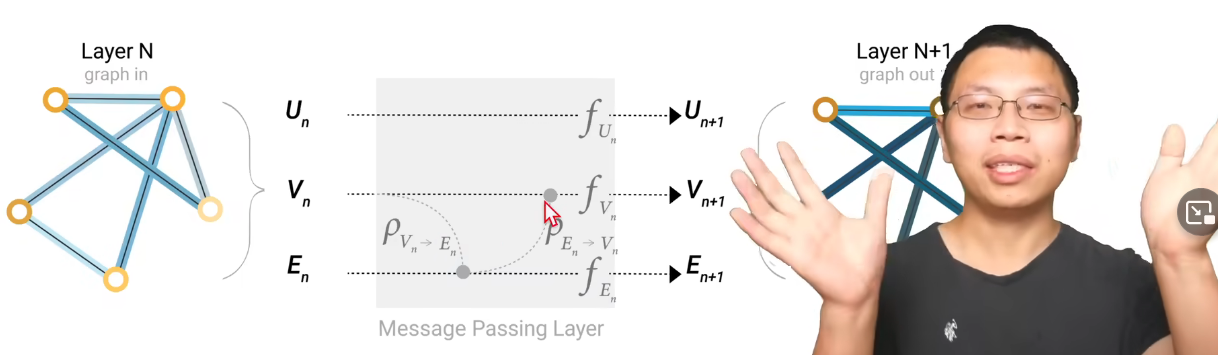
当然这个顺序可以反过来，如下图所示，先从边到顶点再回到边。这两种方式经过实验会导致不一样的结果，但并没有结论说谁比谁好，但是不一样

 

 

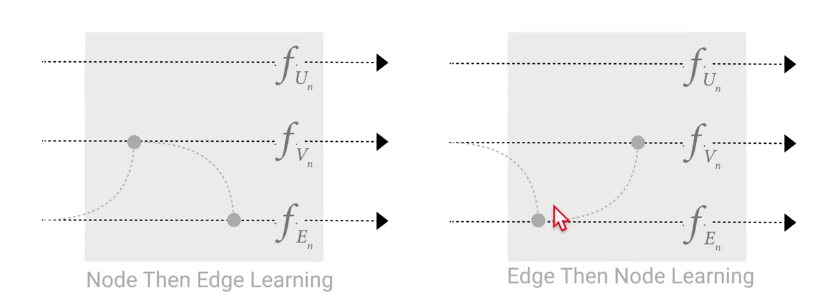
 这个过程也可以交替进行，如下图所示

 

 

 

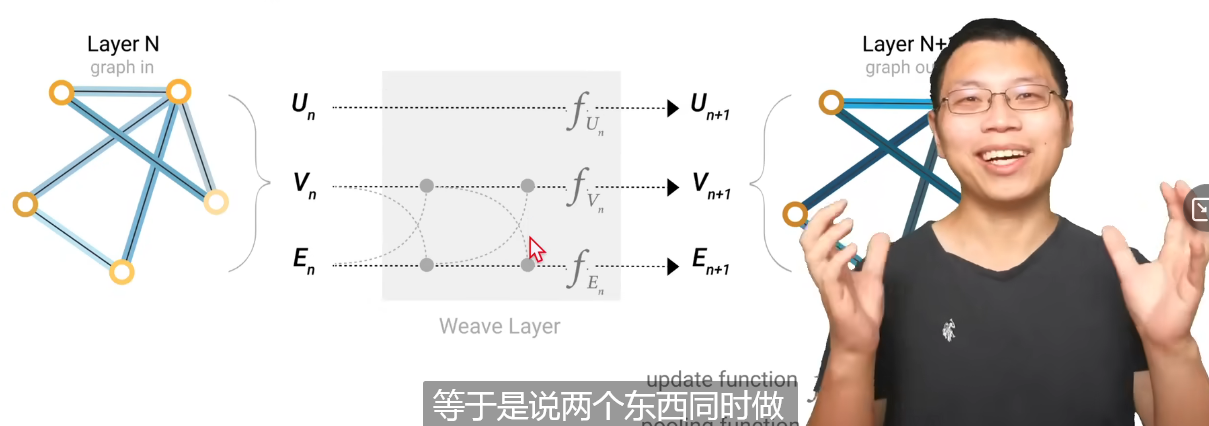
目前讲到这里，并没有讲过为什么会存在一个全局信息

首先，如果一个图结构很大，但边的连接没有那么紧密的时候，会导致一个点的信息要传到另外一个很远的点上需要很多步才能到达。解决方案是加入一个master node(context vector)，即一个虚拟的点，和所有的顶点和边相连（因为顶点和顶点可以直接通过边相连，但很难用具象的方式描述一个点如何与边相连，所以这其实是一个很抽象的概念）。这个东西就是前面说的U（全局信息）它与所有的E和V相连。那么如下图所示，这个时候再做汇聚的时候，会同时汇聚上全局信息。

 

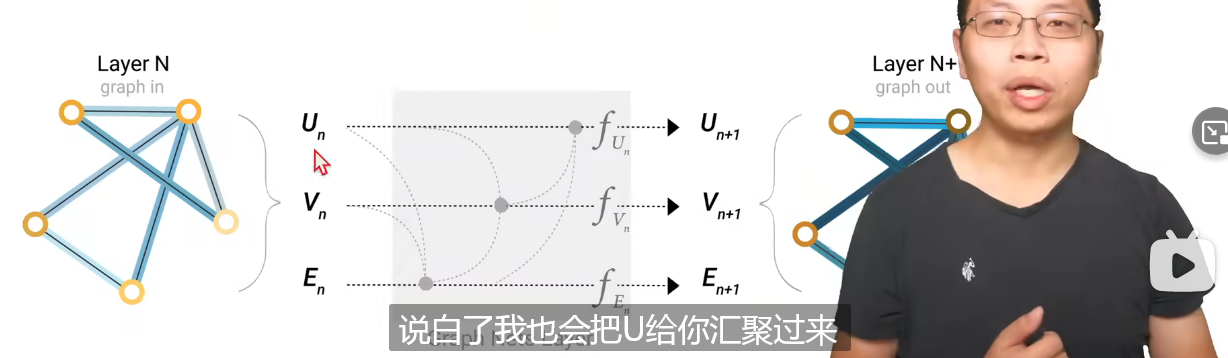
 所以在做预测的时候，可以只用本身的向量，也可以把和它相关的所有边啊顶点啊的信息都拿过来用，对于来自不同类别的属性，汇聚方式可以是加也可以是合并，如下图所示。这个又有一点像attention，相当于用当前的query去找和他相近的东西都拿过来，而图是自己带有结构的，我们本身就知道它和谁比较相近。

 

 

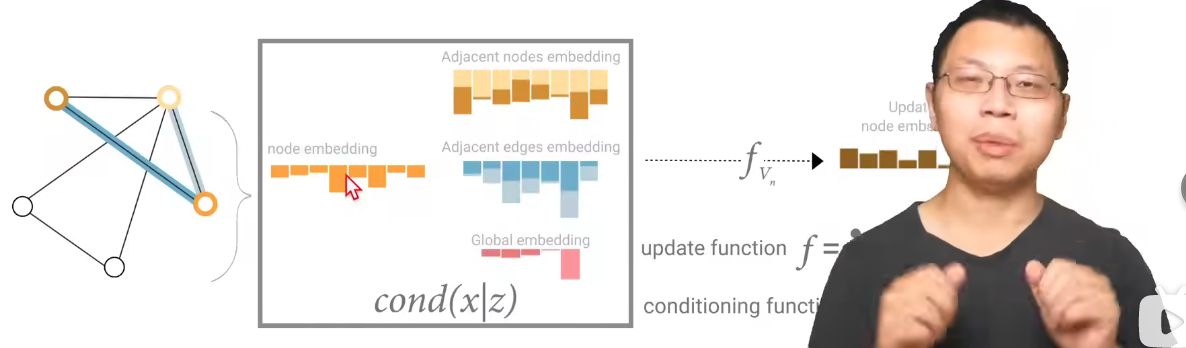
下面这部分只是做一个简单总结，如果做GNN要仔细再看看原视频：

该视频结尾展示了一些超参数调整的统计结果，基本上能得到的结论就是，模型某一方面的复杂度提高一般来说会提高模型性能的上限，但下限一般来说是不变的，所以仍然需要把其他的参数调好才能出效果，否则没有什么区别

此外，汇聚的信息越多整体提升也就越大

 

当GNN有很多层的时候，最后一个图看到的是非常多点的信息，如果该图连通性够的话，可能一个顶点能看到整张图的信息。在计算梯度的时候我们知道要将整个网络中的计算过程的中间变量存下来，那么就会导致这样一个顶点的计算量是无法承受的。所以就提出一个采样的概念，每一次在一个小图上做信息汇聚，也只在小图上算梯度。视频中还介绍了几种采样方法

 

任何神经网络都有一些假设，没有假设就会非常难学习，也就是transformer笔记中提到的归纳偏置

图神经网络的假设就是图的对称性，即不管怎样交换顶点的顺序，GNN对其作用不变

 

GCN（图卷积神经网络，也就是带有汇聚操作的神经网络）作为子图的函数近似：

GCN如果有k个层，每一层都是看1个邻居的话（相当于3*3卷积），那每一层看到的都是一个大小为k的子图（因为层数越深，汇聚的信息越大）

 

之前讲过，图在做汇聚的时候类似于卷积操作，但卷积是加权和。图同样可以做加权和，但卷积的权重与位置相对应，图的顶点的邻居却是没有顺序的，所以图在做汇聚的时候这个权重必须是对位置不敏感的。一个解决办法是借鉴attention，即权重来源于顶点属性的向量表示的关系，而非位置。

 

李沐评价：图是一个非常强大的结构，大多数数据都能表示为一个图，但同时也带来了问题，在图上做优化是非常难的。它本身是一个非常稀疏的架构，如何有效的进行计算是很难的。此外，图网络对超参数非常敏感，需要调优。整体来讲，图神经网络门槛较高。