动态规划股票问题总结

以下题目均使用动态规划进行解答，当然对于前两题直接贪心是没问题的。

1. 买卖股票的最佳时机
2. 买卖股票的最佳时机 II
3. 买卖股票的最佳时机 III
4. 买卖股票的最佳时机 IV
5. 最佳买卖股票时机含冷冻期
6. 买卖股票的最佳时机含手续费

题目详解

dp数组每一个元素的值表示当前状态的利益，更新时，选择利益最大化的操作来更新状态。
例如：

买卖股票的最佳时机

题目类型	1次
dp数组长度	2
dp含义	dp0：未持有股票 dp1：持有股票
dp状态转移	dp0每次都是第一次买，所以无需考虑之前如果卖出的状态。 而dp1是卖出，所以一定依赖于dp0持有时的状态。

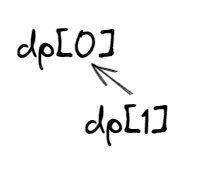
dp0：之前持有股票的利益为dp0，当天购买利益为-prices[i]。
dp1：之前未持有股票（有可能是卖了或没买）的利益为dp1，今天卖的利益为dp0 + prices[i]

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int dp0 = -prices[0];
        int dp1 = 0;
        for(int i = 1;i < prices.length; i++){
            dp0 = Math.max(dp0,-prices[i]);
            dp1 = Math.max(dp1,dp0 + prices[i]);
        }
        return dp1;
    }
}

依赖关系：

买卖股票的最佳时机 II

题目类型	无限次
dp数组长度	2
dp含义	dp0：未持有股票 dp1：持有股票
dp状态转移	dp0每次不一定第一次买，所以需要考虑之前如果卖出的状态（dp1）。 而dp1是卖出，所以一定依赖于dp0持有时的状态。

dp0：之前持有股票的利益为dp0，当天购买利益为**dp1 **- prices[i]。（无限次购买，需要之前未持有的状态，依赖dp1）
dp1：之前未持有股票（有可能是卖了或没买）的利益为dp1，今天卖的利益为dp0 + prices[i]（需要保证昨天持有，依赖于状态dp0）

class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[2];
        // 0表示持有，1表示卖出
        dp[0] = -prices[0];
        dp[1] = 0;
        for(int i = 1; i < prices.length; i++){
            // 前一天持有; 既然不限制交易次数，那么再次买股票时，要加上之前的收益
            dp[0] = Math.max(dp[0], dp[1] - prices[i]);
            // 前一天卖出; 或当天卖出，当天卖出，得先持有
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
        }
        return dp[1];
    }
}

依赖关系：

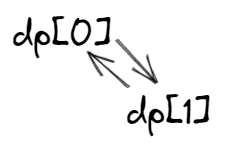
买卖股票的最佳时机含手续费

题目类型	无限次
dp数组长度	2
dp含义	dp0：未持有股票 dp1：持有股票

和上一题相比，执行购买操作时加上手续费即可。

class Solution {
    public int maxProfit(int[] prices,int fee) {
        int[] dp = new int[2];
        // 0表示持有，1表示卖出
        dp[0] = -prices[0] - fee;
        dp[1] = 0;
        for(int i = 1; i < prices.length; i++){
            // 前一天持有; 既然不限制交易次数，那么再次买股票时，要加上之前的收益
            dp[0] = Math.max(dp[0], dp[1] - prices[i] - fee);
            // 前一天卖出; 或当天卖出，当天卖出，得先持有
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
        }
        return dp[1];
    }
}

依赖关系：

买卖股票时机含冷冻期

题目类型	无限次 + 冷冻期
dp数组长度	2
dp含义	dp0：未持有股票 dp1：持有股票

这里只需改变dp0的操作即可，原来的操作为：
dp0 = Math.max(昨天的dp0, 昨天的dp1 - prices[i]);
现在改为
dp0 = Math.max(昨天的dp0, **前天**的dp1 - prices[i]);

class Solution
{
    public int maxProfit(int[] prices)
    {
        if (prices.length == 1) {
            return 0;
        }
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        dp[1][0] = Math.max(-prices[0], -prices[1]);
        dp[1][1] = Math.max(0, dp[0][0] + prices[1]);
        for (int i = 2; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 2][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[prices.length - 1][1];
    }
}

依赖关系：

买卖股票的最佳时机 III

题目类型	2次
dp数组长度	4
dp含义	dp0：第一次持有股票 dp1：未持有股票（已经卖了一次） dp2：第二次持有股票 dp3：未持有股票（已经卖了两次）
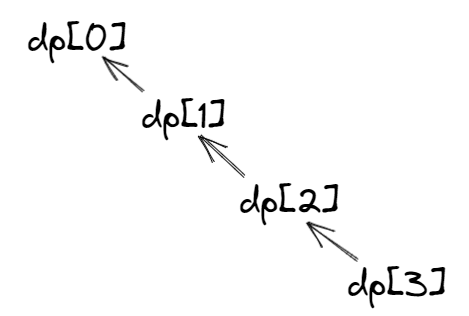
dp状态转移	同之前的题目，dp0这次的状态，直接定义为第一次买，所以无需考虑其他状态。 剩下的状态都会与上一个装填有所关联，所以依次依赖。

class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[4];
        // 1 持有
        // 2 持有后卖出
        // 3 持有后卖出 再持有
        // 4 持有后卖出 再持有再卖出
        dp[0] = -prices[0];
        dp[2] = -prices[0];
        for (int i = 1; i < prices.length; i++) {
            dp[0] = Math.max(dp[0], -prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
            dp[2] = Math.max(dp[2], dp[1] - prices[i]);
            dp[3] = Math.max(dp[3], dp[2] + prices[i]);
        }
        return dp[3];
    }
}

依赖关系：

买卖股票的最佳时机 VI

题目类型	k次
dp数组长度	2 * k
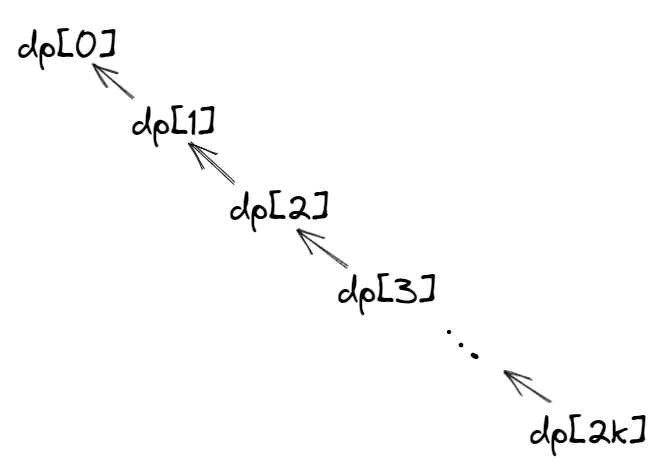
dp含义	dp0：第一次持有股票 dp1：未持有股票（已经卖了一次） dp2：第二次持有股票 dp3：未持有股票（已经卖了两次） dp4：第三次持有股票 依次类推
dp状态转移	同之前的题目，dp0这次的状态，直接定义为第一次买，所以无需考虑其他状态。 剩下的状态都会与上一个装填有所关联，所以依次依赖。

class Solution {
    public int maxProfit(int k, int[] prices) {
        int[] dp = new int[2 * k];
        for (int i = 0; i < dp.length; i += 2) {
            dp[i] = -prices[0];
        }
        for (int i = 1; i < prices.length; i++) {
            for (int j = 0; j < dp.length; j++) {
                int prevStatus = j - 1 >= 0 ? dp[j - 1] : 0;
                dp[j] = Math.max(dp[j], prevStatus + prices[i] * (j % 2 == 0 ? -1 : 1));
            }
        }
        return dp[dp.length - 1];
    }
}

依赖关系：